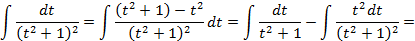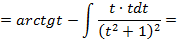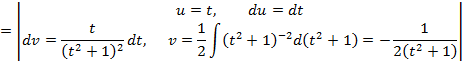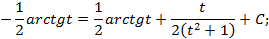Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование простейших рациональных дробей.
Рассмотрим, как интегрируются простейшие (элементарные) рациональные дроби. Интегрирование элементарной дроби вида 1) Для того чтобы вычислить интеграл от элементарной дроби
Интегрирование элементарной дроби вида 2) Учитывая, что
Замечание: Интегралы от элементарных дробей 1) 2) =
Пример 3. 1. Вычислить интеграл: а) Решение. а) 1способ (подведение функции под знак дифференциала) Учитывая, что
2 способ (замена переменной) Сделав замену переменной
б) 1 способ (подведение функции под знак дифференциала) Для начала преобразуем подынтегральную функцию-выделим полный квадрат и заметим, что перед нами простейшая рациональная дробь второго вида, приведём его к табличному виду путем подведения единицы под знак дифференциала:
2 способ (замена переменной)
Интегрирование элементарной дроби вида 3) Дробь третьего вида Для начала преобразуем подынтегральную функцию-выделим полный квадрат в знаменателе
Рассмотрим, как это сделать на примерах. Пример 3.2. Вычислить интеграл: а) Решение.
б) Повторяя аналогичный алгоритм решения имеем:
Замечание: Интегралы от рациональных дробей третьего вида Пример 3.3. Вычислить интеграл Решение.
Интегрирование простейших дробей вида 4)
Интегрирование простейших дробей четвертого вида
Рассмотрим частный случай при Тогда интеграл вида
Учитывая, что
Находим из последнего равенства
Получили рекуррентнуюформулу, позволяющую вычислить интеграл Рассмотрим теперь интеграл от элементарной дроби четвёртого вида в общем случае, то есть интеграл
=
Итак,
Далее к полученному интегралу Рассмотрим на практике интегрирование простейшей дроби четвертого типа. Пример 3.4. Вычислить интеграл Решение. Здесь
Таким образом, Пример 3.5. Вычислить интеграл Решение.
Далее к интегралу
Возвращаясь к старой переменной имеем:
Возвращаясь к исходному интегралу, окончательно имеем:
Замечание: B рациональных дробях вида
Пример 3.6. Вычислить интеграл Решение.
Проинтегрируем отдельно
Возвращаясь к старой переменной, окончательно получим:
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.146.237 (0.024 с.) |
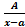 .
. ,достаточно подведения единицу под знак дифференциала
,достаточно подведения единицу под знак дифференциала  :
: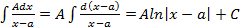 .
.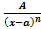 .
.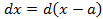 имеем:
имеем: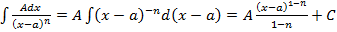 .
. привести к табличным и другим способом, с помощью замены
привести к табличным и другим способом, с помощью замены 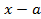 ,просто это займет немного больше времени. Покажем, как это работает:
,просто это займет немного больше времени. Покажем, как это работает: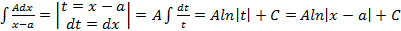 ;
;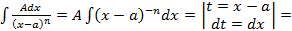
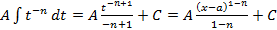 .
.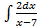 ;б)
;б) 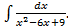
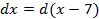 имеем:
имеем: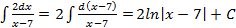 ;
;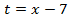 имеем:
имеем: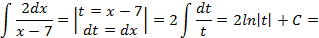
 ;
;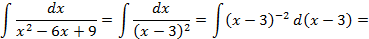
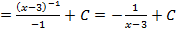 ;
;
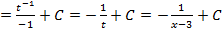 .
.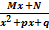 .
.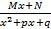 интегрируется
интегрируется  следующим образом:
следующим образом:
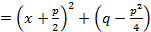 ,так как по условию квадратный трёхчлен
,так как по условию квадратный трёхчлен 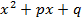 не имеет вещественных корней, то
не имеет вещественных корней, то 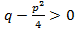 ,обозначим
,обозначим 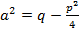 , далее применяем к преобразованному интегралу замену
, далее применяем к преобразованному интегралу замену 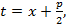

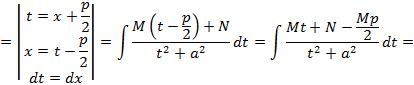
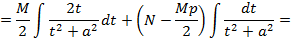
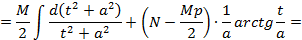
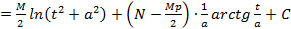 . Последним этапом необходимо вернуться к старой переменной, сделайте это самостоятельно.
. Последним этапом необходимо вернуться к старой переменной, сделайте это самостоятельно.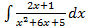 ;б)
;б) 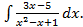
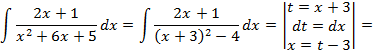


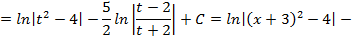
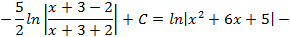
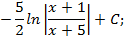
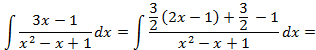

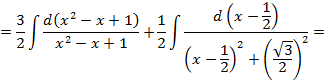
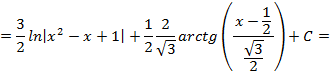
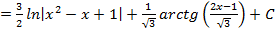 .
.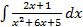 .
. .
.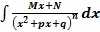 .
.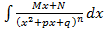 является довольно громоздким, требующим более сложных вычислений.
является довольно громоздким, требующим более сложных вычислений.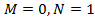 .
.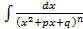 можно путем выделения в знаменателе полного квадрата
можно путем выделения в знаменателе полного квадрата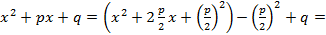
 ,где
,где 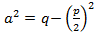 и замены
и замены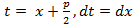 , представить в виде
, представить в виде 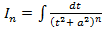 и получить для него рекуррентную формулу. Для этого применим к интегралу
и получить для него рекуррентную формулу. Для этого применим к интегралу 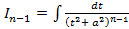 формулу интегрирования по частям:
формулу интегрирования по частям: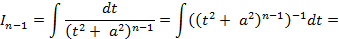
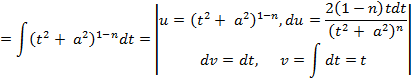
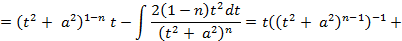

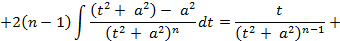
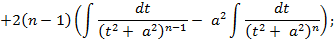
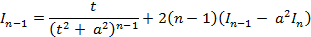

 :
: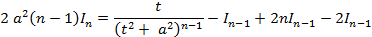
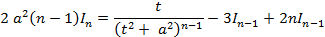
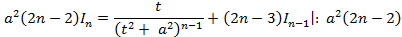
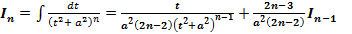 (3.2)
(3.2) .
.
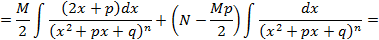
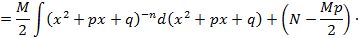



 .
.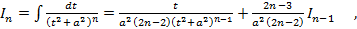 в нашем случае
в нашем случае 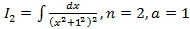 ,поэтому имеем:
,поэтому имеем: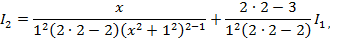
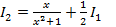 ,где
,где 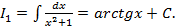
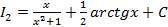 .
. .
.

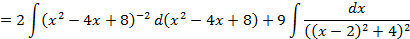

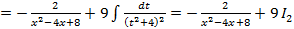 ;
;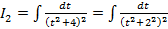 , где
, где 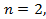
 применяется рекуррентная формула
применяется рекуррентная формула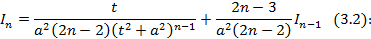
 ,
,  где
где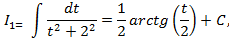

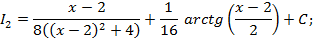

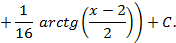
 можно обойтись и без рекуррентной формулы (3.2), преобразовав подынтегральное выражение и применив формулу интегрирование по частям. Рассмотрим, как это сделать на примере 3.6.
можно обойтись и без рекуррентной формулы (3.2), преобразовав подынтегральное выражение и применив формулу интегрирование по частям. Рассмотрим, как это сделать на примере 3.6.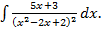

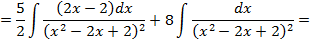
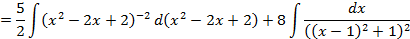
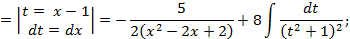
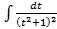 :
: