
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение интеграла на алгебраическую сумму.Стр 1 из 7Следующая ⇒
Аннотация
Учебно-методическое пособие по одному из самых больших и сложных разделов высшей математики интегрирование предназначено для преподавателей и студентов всех технических направлений подготовки бакалавриата. Содержит теоретический материал, методические рекомендации по решению задач, типовые задачи с подробными решениями, варианты типовых заданий по разделу «Интегральное исчисление функций одной переменной». Составлено для проведения теоретических и практических работ по дисциплине «Высшая математика». Студентам это пособие поможет подготовиться к практическим, рейтинговым занятиям по данному разделу, а преподавателю сэкономит время на подготовку практических и домашних заданий.
Автор
Оглавление ГЛАВА1. Первообразная и неопределённый интеграл 4 1.1. Понятие первообразной и неопределенного интеграла….. 4 1.2. Свойства неопределенного интеграла. 6 1.3. Таблица основных неопределенных интегралов..9 ГЛАВА 2. Основные методы интегрирования. 14 2.1. Метод непосредственного интегрирования. 14 2.2. Метод замены переменных. 19 2.3. Метод интегрирование по частям. 25 ГЛАВА3. Методы интегрирования различных классов функций 30 3.1. Интегрирование рациональных функций.30 3.2. Интегрирование тригонометрических функций. 54 3.3. Интегрирование некоторых иррациональных функций. 62 3.4. «Берущиеся» и «не берущиеся» интегралы. 68 ГЛАВА 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. 71 4.1. Определение определенного интеграла и геометрический смысл. 71 4.2. Формула Ньютона-Лейбница. 74 4.3. Свойства определенного интеграла. 77 4.4. Методы вычисления определенного интеграла. 84 4.5. Несобственные интегралы. 91 ГлАВА 5. Приложения определенного интеграла. 106 5.1. Вычисление площадей плоских фигур. 106 5.2. Вычисление длины дуги плоской кривой. 116 5.3. Вычисление объемов тел вращения. 123 Литература. 131
ГЛАВА1. Первообразная и неопределённый интеграл 1.1. Понятие первообразной и неопределенного интеграла. Одной из основных задач дифференциального исчисления как мы уже знаем является отыскание производной заданной функции. Разнообразные вопросы математического анализа и его приложения в геометрии, механике, физике и технике приводят к обратной задаче: по данной функции
Таким образом, восстановление функции по известной производной этой функции - одна из задач интегрального исчисления. Функция Пример 1.1. Показать, что функция Решение. Так как
Теорема 1.1. Если функция Доказательство. Если функция Пусть функция
Совокупность всех первообразных Обозначение: Функция Операция нахождения первообразной для данной функции называется интегрированием.
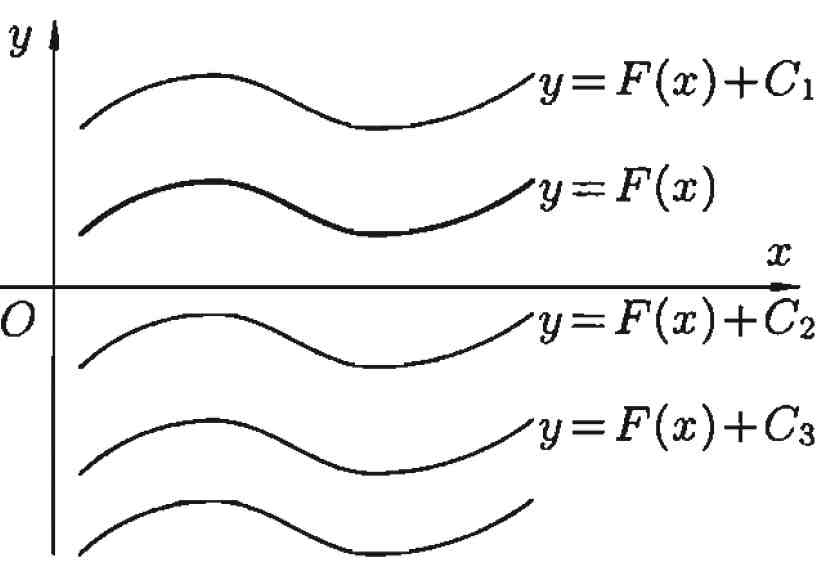 Геометрический смысл неопределенного интеграла – это семейство параллельных интегральных кривых Геометрический смысл неопределенного интеграла – это семейство параллельных интегральных кривых 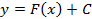 ,где каждому числовому значению ,где каждому числовому значению 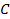 соответствует определенная кривая семейства(рис.1.). соответствует определенная кривая семейства(рис.1.).
График каждой первообразной (кривой) называется интегральной кривой. Замечание: -Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке. 1.2. Свойства неопределенного интеграла. Отметим свойства неопределенного интеграла, вытекающие из его определения. 1. Производная неопределенного интеграла равна подынтегральной функции, то есть
Доказательство.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, то есть
Доказательство.
Замечание: Из данных свойств, следует, что интегрирование является обратной операцией к дифференцированию, обратное так же верно.
Пример 1.2. Проверить верно ли равенство Решение.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции, то есть
Доказательство.
4. Неопределенный интеграл от суммы (разности) функций равен сумме(разности) неопределенных интегралов от этих функций, то есть
Доказательство. Действительно, пусть
Замечание: Это свойство справедливо для любого конечного числа слагаемых функций. 5. Постоянный множитель можно выносить за знак интеграла, то есть
Доказательство.
Замечание: Свойства 4 и 5 можно объединить в одно и получить равенство
6. Инвариантностьформулыинтегрирования: Если Доказательство. Пусть
Таким образом, любая формула интегрирования остается справедливой при подстановке вместо независимой переменной любой дифференцируемой функции. Так, например, в формуле Заменим В частности, например,
1.3. Таблица неопределенных интегралов. Пользуясь тем, что действие обратное интегрированию дифференцирование, можно составить таблицу основных интегралов с помощью которой получаем различные значения неопределенных интегралов от заданных функций.
Таблица основных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. «Длинный» логарифм:
14. «Высокий» логарифм:
Интегралы в выше приводимой таблице называются табличными. Их следует знать наизусть. Вывод этих формул сводится к проверке того, что дифференциал правой части равен подынтегральному выражению в левой части равенства, и не представляет особого труда показать это для всех формул, докажем,например, справедливость формул 4, 8,12: 4) а) Если
б) Если
В обоих случаях получили подынтегральную функцию
12)
Пример 1.3. Используя таблицу и основные свойства неопределенных интегралов найти интеграл: а) в)
Решение. а) В таблице интегралов - интеграла от корня нет, зато есть интеграл от степенной функции (формула 3 в таблице интегралов), поэтому переходя от корня к степени и интегрируя, получим:
б) Применяя свойства неопределенного интеграла и табличные формулы 3, 5,2 соответственно, имеем:
При каждом интегрировании мы получаем свою произвольную постоянную, но нет необходимости писать её при вычислении каждого интеграла. Достаточно написать ее после выполнений всех интегрирований, так как сумма (разность) постоянных является постоянной
в) Применяя свойства неопределенного интеграла и табличные формулы, получим:
Пример 1.4. Вычислить интеграл Решение.
Проверка:
ГЛАВА2. Основные методы интегрирования При интегрировании нет какого–либо общего приема вычисления интеграла. Имеется лишь ряд методов, позволяющих свести данный интеграл к табличному виду. Такими методами являются: метод непосредственного интегрирования, метод замены переменной и метод интегрирования по частям. 2.1. Метод непосредственного интегрирования. Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Данный метод включает два основных приема: 1) разложение интеграла на алгебраическую сумму;2) подведение функции под знак дифференциала. Эти приемы могут быть использованы как самостоятельно, так и в совокупности. Разберем каждый прием в отдельности, а затем рассмотрим совместное их применение. Ответы: 1.1. 1.3. 1.5. 1.19. 2. Методом подведением функции под знак дифференциала вычислить интегралы:
Ответы: 2.1. 2.3. 2.5. 2.16. 2.20. 2.22. 3.Вычислить интегралы от выражений содержащих квадратный трехчлен:
Ответы: 3.1. 3.3. 3.5. 3.14. 3.22.
4.Вычислить интегралы от выражений содержащих квадратных трехчлен:
Ответы: 4.1. 4.26. 5.Найти интегралы методом замены переменной:
Ответы: 5.1. 5.3. 5.5. 6.Найти интегралы, используя формулу интегрирование по частям:
Ответы: 6.1. 6.26.
ГЛАВА 3. Методы интегрирования различных классов функций Рассмотрим методы интегрирования различных классов функций: дробно-рациональных, иррациональных, тригонометрических функций. Интегралы от данных функций сводятся к табличным соответствующей подстановкой для данного типа подынтегрального выражения. 3.1. Интегрирование рациональных функций. Дробно-рациональной функций (рациональной дробью) называется функция, равная отношению двух многочленов, то есть функция вида
где Рациональная дробь называется правильной, если Например, дробь
| Поделиться:
| |
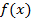 найти такую функцию
найти такую функцию 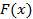 ,производная от которой была бы равна функции
,производная от которой была бы равна функции 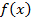 , то есть
, то есть 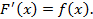
 , если для любого
, если для любого 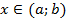 выполняется равенство:
выполняется равенство: 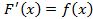 .
.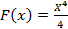 является первообразной для функции
является первообразной для функции 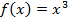 .
.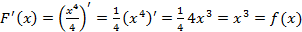 , следовательно
, следовательно 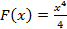 является первообразной для функции
является первообразной для функции , где
, где  , так как
, так как 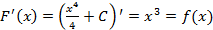 .
.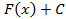 , где
, где 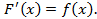
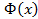 любая другая первообразная для функции
любая другая первообразная для функции  на
на  , то есть
, то есть 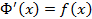 . Тогда для любого
. Тогда для любого  имеем:
имеем: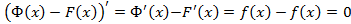 , отсюда
, отсюда 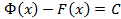 , тогда
, тогда 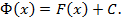
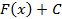 , где
, где 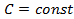 называют неопределенным интегралом от функции
называют неопределенным интегралом от функции 

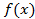 называется подынтегральной функцией,
называется подынтегральной функцией,  подынтегральное выражение,
подынтегральное выражение,  переменная интегрирования,
переменная интегрирования, 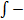 знак неопределенного интеграла.
знак неопределенного интеграла.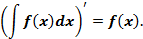
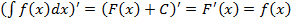 .
.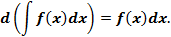

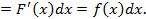
 .
.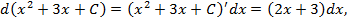 дифференциал правой части исходного равенства совпадает с подынтегральным выражением в левой части ,следовательно равенство верно.
дифференциал правой части исходного равенства совпадает с подынтегральным выражением в левой части ,следовательно равенство верно.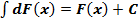 .
.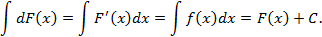
 .
.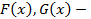 первообразные для функций
первообразные для функций 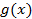 соответственно, то есть
соответственно, то есть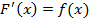 и
и 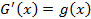 , тогда
, тогда
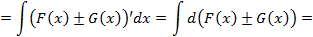
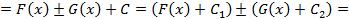
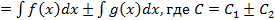 .
. , где
, где 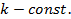

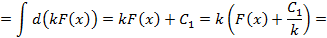
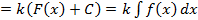 ,где
,где 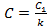 .
.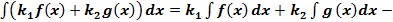 свойство линейно сти неопределённого интеграла, данное равенство справедливо для любого конечного числа слагаемых функций.
свойство линейно сти неопределённого интеграла, данное равенство справедливо для любого конечного числа слагаемых функций.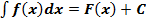 , то
, то 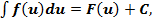
 где
где 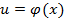 произвольная функция, имеющая непрерывную производную.
произвольная функция, имеющая непрерывную производную.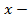 независимая переменная,
независимая переменная, 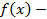 непрерывная функция и
непрерывная функция и 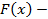 её первообразная, тогда как нам уже известно
её первообразная, тогда как нам уже известно 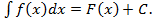 Положим теперь
Положим теперь 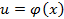 , где
, где 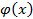 -непрерывно- дифференцируемая функция. Рассмотрим сложную функцию
-непрерывно- дифференцируемая функция. Рассмотрим сложную функцию 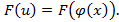 В силу инвариантности дифференциала функции имеем:
В силу инвариантности дифференциала функции имеем: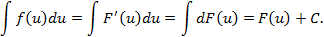
 вместо буквы
вместо буквы 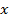 при интегрировании может быть использована любая другая буква, например
при интегрировании может быть использована любая другая буква, например 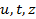 и так далее.
и так далее.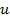 имеем:
имеем: 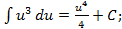

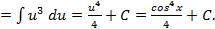

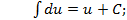
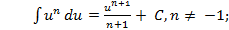
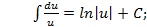
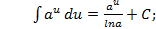
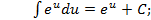
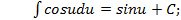
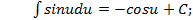
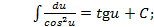
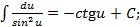
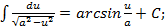



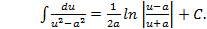
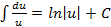 , подынтегральная функция
, подынтегральная функция  определена для всех значений
определена для всех значений 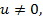 возможны два случая:
возможны два случая: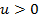 , то
, то 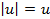 и
и  , то
, то 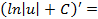
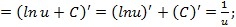
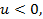 то
то 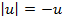 и
и 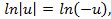 то
то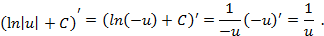
 получена подынтегральная функция, значит, формула справедлива;
получена подынтегральная функция, значит, формула справедлива;
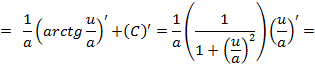
 - получили подынтегральную функцию, формула верна.
- получили подынтегральную функцию, формула верна.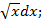 б)
б) 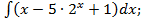
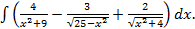
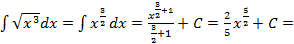
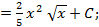
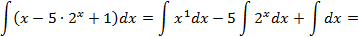
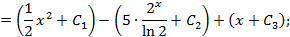
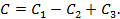 Таким образом, имеем:
Таким образом, имеем: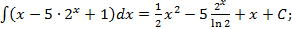

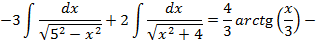
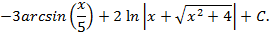
 и проверить результат дифференцированием.
и проверить результат дифференцированием.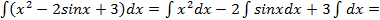
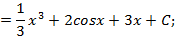

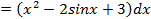 ,дифференциал правой части полученного равенства совпадает с подынтегральным выражением исходного равенства – значит, интеграл вычислен правильно.
,дифференциал правой части полученного равенства совпадает с подынтегральным выражением исходного равенства – значит, интеграл вычислен правильно.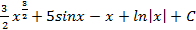 ; 1.2.
; 1.2. 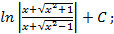
 ; 1.4.
; 1.4. 
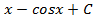 ; 1.6.
; 1.6. 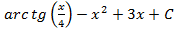 ; 1.7.
; 1.7. 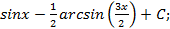 1.8.
1.8. 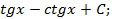 1.9.
1.9. 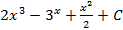 ; 1.10.
; 1.10.  ; 1.11.
; 1.11. 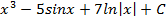 ; 1.12.
; 1.12. 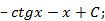 1.13.
1.13. 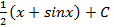 ; 1.14.
; 1.14. 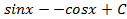 ; 1.15.
; 1.15. 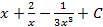 ; 1.16.
; 1.16. 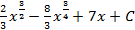 ; 1.17.
; 1.17. 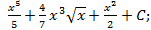 1.18.
1.18. 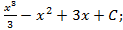
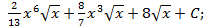 1.20.
1.20. 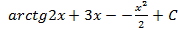 ; 1.21.
; 1.21.  ; 1.22.
; 1.22.  1.23.
1.23. 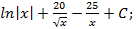 1.24.
1.24.  1.25.
1.25. 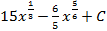 ; 1.26.
; 1.26. 
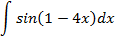
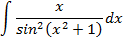


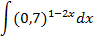
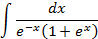
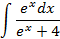

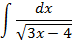
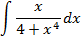
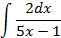
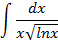

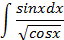
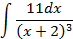
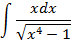
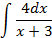
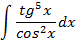
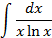
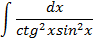
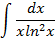
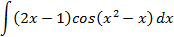
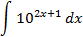
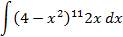
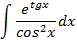

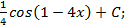 2.2.
2.2. 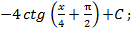
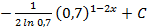 ; 2.4.
; 2.4. 
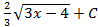 ; 2.6.
; 2.6. 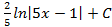 ; 2.7.
; 2.7. 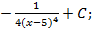 2.8.
2.8. 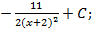 2.9.
2.9. 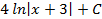 ; 2.10.
; 2.10.  2.11.
2.11. 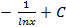 ; 2.12.
; 2.12. 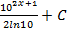 ; 2.13.
; 2.13. 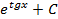 ; 2.14.
; 2.14.  ; 2.15.
; 2.15. 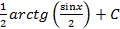 ;
;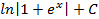 ; 2.17.
; 2.17. 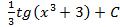 ; 2.18.
; 2.18. 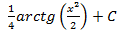 ; 2.19.
; 2.19. 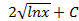 ;
;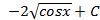 ; 2.21.
; 2.21. 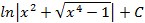 ;
;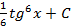 ; 2.23.
; 2.23. 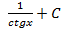 ; 2.24.
; 2.24.  ; 2.25.
; 2.25. 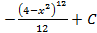 ; 2.26.
; 2.26. 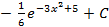 .
.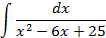
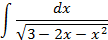
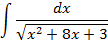
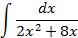
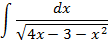

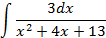

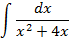

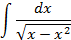
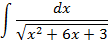

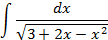



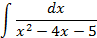

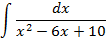

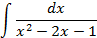
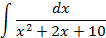
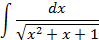
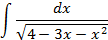
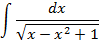
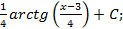 3.2.
3.2. 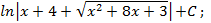
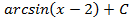 ; 3.4.
; 3.4. 
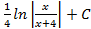 ; 3.6
; 3.6 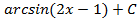 ; 3.7.
; 3.7. 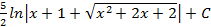 ; 3.8.
; 3.8. 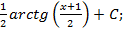 3.9.
3.9. 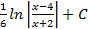 ; 3.10.
; 3.10. 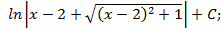 3.11.
3.11.  ; 3.12.
; 3.12. 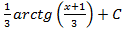 ; 3.13.
; 3.13. 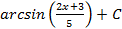 ;
; ; 3.15.
; 3.15.  ; 3.16.
; 3.16. 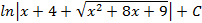 ; 3.17.
; 3.17. 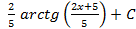 ; 3.18.
; 3.18. 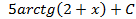 ; 3.19.
; 3.19. 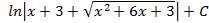 ; 3.20.
; 3.20.  3.21.
3.21. 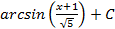 ;
; ; 3.23.
; 3.23. 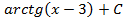 ; 3.24.
; 3.24. 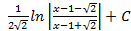 ; 3.25.
; 3.25.  ; 3.26.
; 3.26.  .
.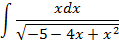
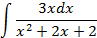
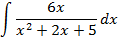
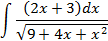
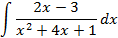
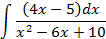
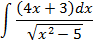
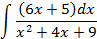

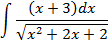
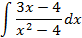
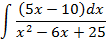
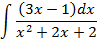

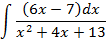
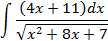
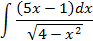




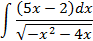
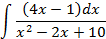
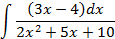
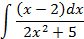

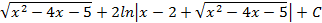 ; 4.2.
; 4.2. 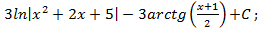 4.3.
4.3.  ; 4.4.
; 4.4.  4.5.
4.5. 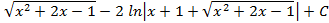 ; 4.6
; 4.6 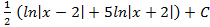 ; 4.7.
; 4.7.  ; 4.8.
; 4.8. 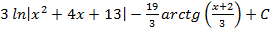 ; 4.9.
; 4.9. 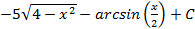 ; 4.10.
; 4.10. 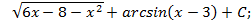 4.11.
4.11. 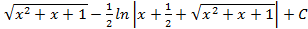 ; 4.12.
; 4.12. 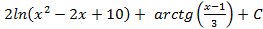 ; 4.13.
; 4.13.  ; 4.14.
; 4.14. 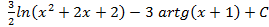 ; 4.15.
; 4.15.  4.16.
4.16. 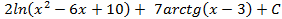 ; 4.17.
; 4.17. 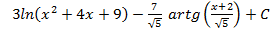 ; 4.18.
; 4.18. 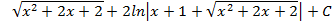 ; 4.19.
; 4.19. 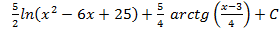 ; 4.20.
; 4.20. 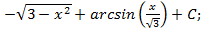 4.21.
4.21. 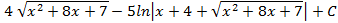 ; 4.22.
; 4.22. 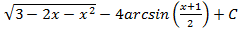 ; 4.23.
; 4.23. 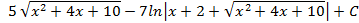 ; 4.24.
; 4.24. 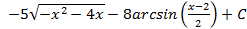 ; 4.25.
; 4.25. 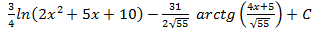 ;
;
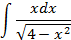
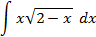
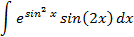
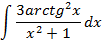
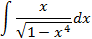
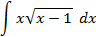

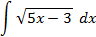
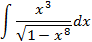
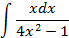
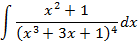
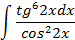
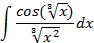
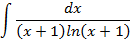
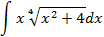
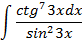
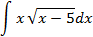


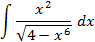
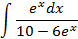
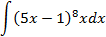
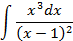
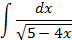
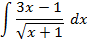
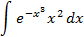
 5.2.
5.2. 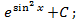
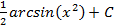 ; 5.4.
; 5.4. 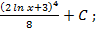
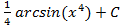 ; 5.6.
; 5.6. 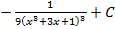 ; 5.7.
; 5.7. 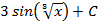 ; 5.8.
; 5.8. 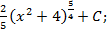 5.9.
5.9.  5.10.
5.10.  5.11.
5.11. 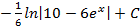 ; 5.12.
; 5.12.  ; 5.13.
; 5.13. 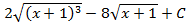 ; 5.14.
; 5.14. 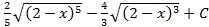 ; 5.15.
; 5.15.  ; 5.16.
; 5.16. 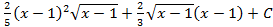 ; 5.17.
; 5.17. 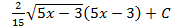 ; 5.18.
; 5.18. 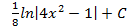 ; 5.19.
; 5.19. 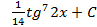 ; 5.20.
; 5.20. 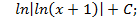 5.21.
5.21. 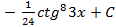 ; 5.22.
; 5.22. 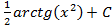 ; 5.23.
; 5.23. 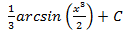 ; 5.24.
; 5.24.  ; 5.25.
; 5.25. 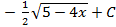 ; 5.26.
; 5.26. 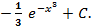
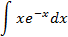

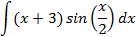
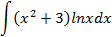
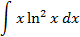

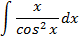
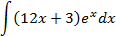
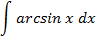
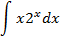
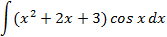

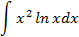
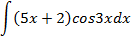

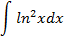
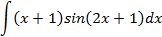
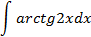
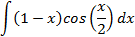
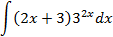

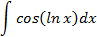

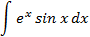
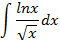

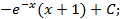 6.2.
6.2. 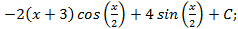 6.3.
6.3. 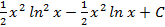 ; 6.4.
; 6.4. 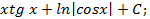 6.5.
6.5.  ; 6.6
; 6.6 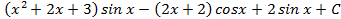 ; 6.7.
; 6.7.  ; 6.8.
; 6.8. 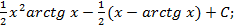 6.9.
6.9.  6.10.
6.10. 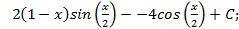 6.11.
6.11. 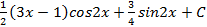 ; 6.12.
; 6.12. 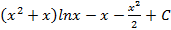 ; 6.13.
; 6.13. 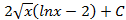 ; 6.14.
; 6.14.  ; 6.15.
; 6.15.  ; 6.16.
; 6.16. 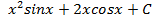 ; 6.17.
; 6.17.  ; 6.18
; 6.18  ; 6.19.
; 6.19. 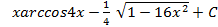 ; 6.20.
; 6.20. 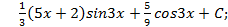 6.21.
6.21. 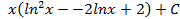 ; 6.22.
; 6.22.  ; 6.23.
; 6.23.  ; 6.24.
; 6.24.  ; 6.25.
; 6.25.  ;
;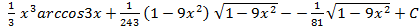 .
. (3.1),
(3.1),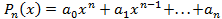 ,
,  многочлены от переменной
многочлены от переменной 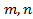 соответственно,
соответственно, 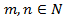 -натуральные числа.
-натуральные числа.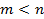 и неправильной, если
и неправильной, если  .
.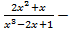 правильная, так как
правильная, так как 


