
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование по частям в определенном интеграле.
При выводе формулы интегрирования по частям в неопределенном интеграле было получено равенство
Формула (4.5) называется формулой интегрирования по частям в определенном интеграле. Пример 4.5. Вычислить интеграл: а) б) Решение. а) Интегрируем по частям, получим:
б)
в)
4.5.Интегрирование четных и нечетных функций в симметричных пределах интегрирования. Пусть функция
Разобьем отрезок интегрирования
Сделаем в первом интеграле(в сумме) подстановку
Вернемся к равенству (4.7):
Если функция
Если функция
Таким образом, равенство (4.7) принимает вид (4.6).
Пример 4.6. Вычислить интеграл Решение. Подынтегральная функция
Пример 4.7. Найти интегралы: а) б) Решение. а)Благодаря формуле (4.6) можно не вычисляя интеграл сказать, что он равны нулю, так как, подынтегральная функция Итак, б) в)Аналогично,
4.6. Несобственные интегралы. Интеграл Например, интеграл Непрерывность функции является достаточным условием ее интегрируемости, но определенный интеграл может существовать и для некоторых разрывных функций на данном промежутке. Рассмотрим так называемые несобственные интегралы. Различают несобственные интегралы первого и второго рода. Несобственные интегралы первого рода - это случаи определённых интегралов от непрерывной функции на заданном промежутке интегрирования, но с бесконечным верхним или нижним пределом интегрирования, или с двумя бесконечными пределами. Несобственные интегралы второго рода -это случаи определенных интегралов с конечными промежутками интегрирования, ноот функций, имеющих бесконечный разрыв в нижнем или верхнем пределе интегрирования или в обоих пределах(и в нижнем и в верхнем), или во внутренней точке интервала интегрирования. Разберём эти случаи поподробно.
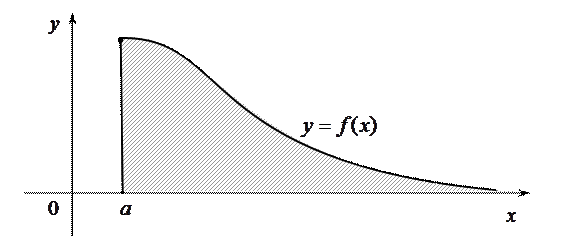
Несобственные интегралы первого рода (интегралы с бесконечными пределами интегрирования). Пусть, функция Обозначение: Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае интеграл называется расходящимся и ему не приписывается никакого значения. Замечание: Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции (рис.3)
Рис.3 Аналогично определяется несобственные интеграл на промежутке Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом
Замечание: В качестве внутренней точки удобно взять значение
Пример 4.8. Вычислить несобственные интегралы или установить их расходимость: а)
Решение. а)
б)
в)Поскольку оба предела интегрирования (верхний и нижний) бесконечны разбиваем интеграл на два несобственных интеграла, если они оба сходятся, то исходный интеграл сходится:
Под знаком интеграла рациональная дробь, поэтому применяя алгоритм интегрирования рациональных дробей, получим:
(так как, знаменатель полученной дроби имеет комплексные корни
Получим систему
Пример 4.9. При каких значениях Решение. Если
Если Таким образом, интеграл
Замечание: В некоторых задачах нет необходимости вычислять интеграл. Достаточно лишь знать, сходится он или расходится. Сформулируемпризнаки сходимости несобственных интегралов первого рода.
Теорема 4.3. (признак сравнения). Если на промежутке
Теорема 4.4. (предельный признак). Если существует предел (
Замечание: В качестве эталона для сравнения функций часто берут функцию
Пример 4.10. Исследовать сходимость интеграла: а) г) Решение. а)Сравним функцию б)Здесь подынтегральная функция
следовательно исходный интеграл Оставшиеся несобственные интегралы: в) рекомендуется исследовать на сходимость самостоятельно, для закрепления изученного материала. Несобственные интегралы второго рода. Пусть функция Обозначение:
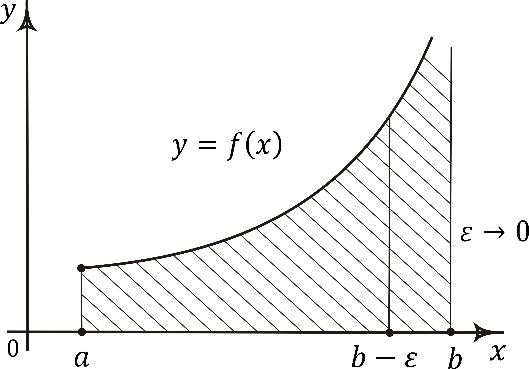
Рис.4 Замечание: Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции (рис.4)
Аналогично, если функция Если функция
Если сходятся оба интеграла справа, то сходится и суммарный интеграл слева.
Замечание: Точек разрыва внутри отрезка может быть несколько. В частности, если подынтегральная функция разрывна на концах интервала то есть одновременно при и
Пример 4.11. Вычислить несобственные интегралы второго рода или установить их расходимость: а) Решение. а) Так как подынтегральная функция
следовательно, исходный интеграл расходится; б) Подынтегральная функция
в) Подынтегральная функция
интеграл слева расходится, так как оба интеграла справа расходятся ( г)Подынтегральная функция
Пример 4.1 2. При каких значениях Решение. Функция Если Если
Таким образом, интеграл сходится Замечание: В некоторых задачах интегрирования нет необходимости вычислять интеграл, достаточно установить его сходимость или расходимость. Сформулируемпризнаки сходимости несобственных интегралов второго рода.
Теорема 4.5. (признак сравнения) Пусть непрерывные на промежутке
Теорема 4.6. (предельный признак) Пусть функции Замечание: В качестве эталона для сравнения функций часто берут функцию
Пример 4.13. Исследовать сходимость интеграла: а) Решение. а) Подынтегральная функция б) Следующие несобственные интегралы, для закрепления изученного материала, рекомендуется исследовать на сходимость самостоятельно:: в) Задания для самостоятельного решения 10. Вычислить определенный интеграл по формуле Ньютона-Лейбница, применив один из методов интегрирования:
Ответы: 10. 1. 10.10. 10.15. 10.21. 10.26 11. Вычислить несобственные интегралы первого рода или установить их расходимость:
Ответы: 11.1. 12. Вычислить несобственные интегралы второго рода или установить их расходимость:
Ответы: 12.1. расходится; 12.2. 12.5. 12.9. расходится; 12.10. расходится; 12.11.
ГлАВА 5. Приложения определенного интеграла Определённый интеграл используется в различных приложениях: при вычислении площадей плоских фигур, длин дуг плоских кривых, объемов тел вращения и др. 5.1. Вычисление площадей плоских фигур
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.157 с.) |
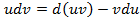 . Проинтегрировав его в пределах от
. Проинтегрировав его в пределах от 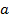 до
до 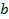 в соответствии со свойствами определенного интеграла имеем:
в соответствии со свойствами определенного интеграла имеем: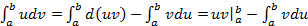 ; или
; или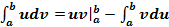 (4.5)
(4.5)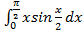 ;
;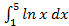 ;в)
;в) 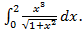
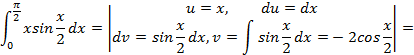
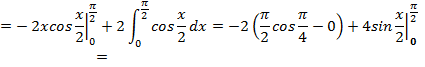
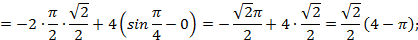
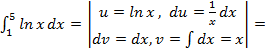
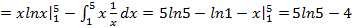 .
.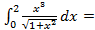
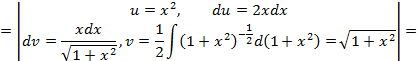
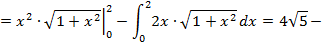
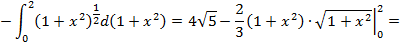
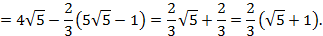
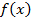 непрерывна на отрезке
непрерывна на отрезке  симметричном относительно
симметричном относительно 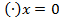 . Докажем, следующее:
. Докажем, следующее: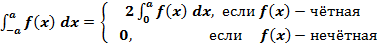 (4.6)
(4.6)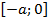 и
и 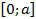 .Тогда используя свойства определенного интеграла имеем:
.Тогда используя свойства определенного интеграла имеем: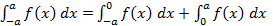 (4.7)
(4.7)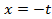 получим:
получим: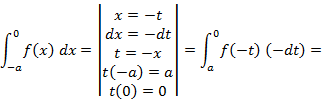
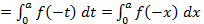 (определенный интеграл не зависит от обозначения переменной интегрирования);
(определенный интеграл не зависит от обозначения переменной интегрирования);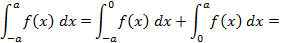
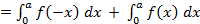 ;
;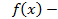 чётная, то есть
чётная, то есть 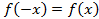 ,то
,то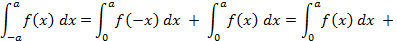
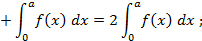
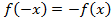 ,то
,то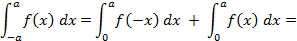
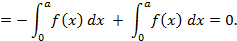
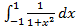 .
.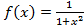 является четной, так как
является четной, так как 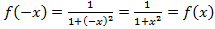 . Следовательно, по формуле (4.6) получим:
. Следовательно, по формуле (4.6) получим: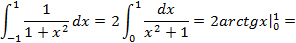
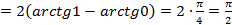 .
.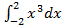 ;
; 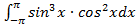 ; в)
; в) 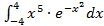 .
.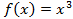 нечетная,
нечетная,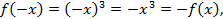 а пределы интегрирования симметричны.
а пределы интегрирования симметричны.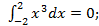
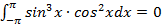 , так как функция
, так как функция 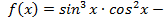 нечётная,
нечётная, 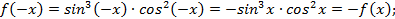
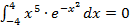 ,
, 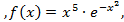

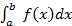 , где промежуток интегрирования
, где промежуток интегрирования 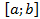 конечный, а подынтегральная функция
конечный, а подынтегральная функция  непрерывна на отрезке
непрерывна на отрезке 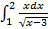 не существует, поскольку отрезок интегрирования
не существует, поскольку отрезок интегрирования 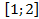 не входит в область определения подынтегральной функции
не входит в область определения подынтегральной функции 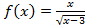 ,действительно, область определения исходной функции удовлетворяет системе уравнений
,действительно, область определения исходной функции удовлетворяет системе уравнений 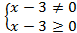 ,то есть удовлетворяет неравенству
,то есть удовлетворяет неравенству 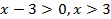 .
.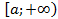 (рис.3). Если существует конечный предел
(рис.3). Если существует конечный предел 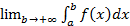 , то его называют несобственным интегралом первого рода.
, то его называют несобственным интегралом первого рода.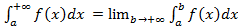 .
.
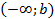 :
: 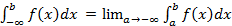 ;
;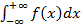 , нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой - с конечным нижним пределом интегрирования:
, нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой - с конечным нижним пределом интегрирования: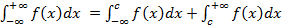 ,где
,где 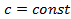 , интеграл слева сходится, если сходятся оба интеграла справа.
, интеграл слева сходится, если сходятся оба интеграла справа.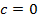 при условии, что подынтегральная функция непрерывна в этой точке.
при условии, что подынтегральная функция непрерывна в этой точке.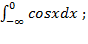 б)
б) 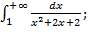 в)
в) 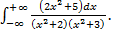
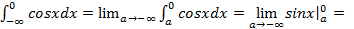
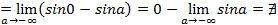 , так как при
, так как при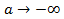 функция
функция 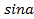 не имеет предела, следовательно, интеграл расходится;
не имеет предела, следовательно, интеграл расходится;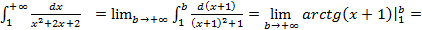

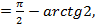 интеграл сходится;
интеграл сходится;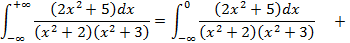
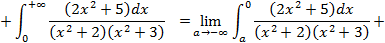
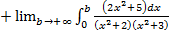 , но в данном случае это не рационально, так как подынтегральная функция
, но в данном случае это не рационально, так как подынтегральная функция 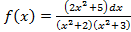 является четной
является четной 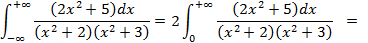
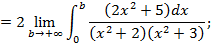
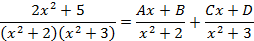
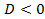 )
)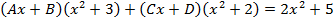
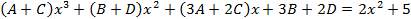
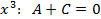

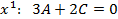
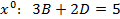
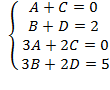 , решая её получим
, решая её получим 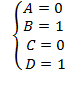 .Коэффициенты найдены, вернемся к вычислению предела:
.Коэффициенты найдены, вернемся к вычислению предела: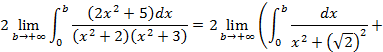
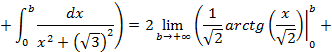
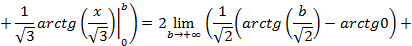
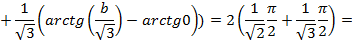
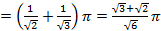 .
.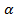 несобственный интеграл
несобственный интеграл 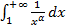 сходится и при каких расходится?
сходится и при каких расходится?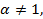 то
то 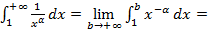
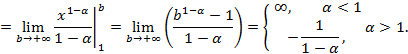
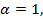 то
то 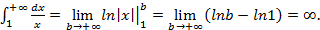
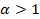 и расходится при
и расходится при 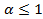 .
.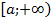 непрерывные функции
непрерывные функции 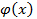 удовлетворяют условию
удовлетворяют условию 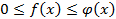 и интеграл
и интеграл 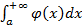 сходится, то
сходится, то 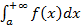 тоже сходится, а из расходимости интеграла
тоже сходится, а из расходимости интеграла 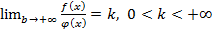 ,
,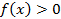 ,
, 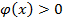 ), то интегралы
), то интегралы 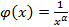 .В примере 4.9 показано, что несобственный интеграл
.В примере 4.9 показано, что несобственный интеграл 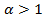 и расходится при
и расходится при 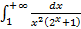 ;б)
;б) 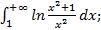 в)
в) 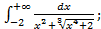
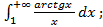 д)
д) 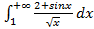 .
.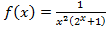 с функцией
с функцией 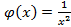 .Как известно, интеграл
.Как известно, интеграл 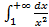 сходится, так как
сходится, так как 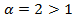 .На промежутке
.На промежутке 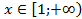 имеем
имеем 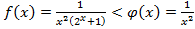 ,следовательно интеграл
,следовательно интеграл 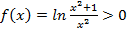 , при
, при 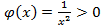 , интеграл от которой сходиться
, интеграл от которой сходиться 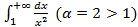 . А так как существует предел
. А так как существует предел 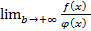 (используем предельный признак):
(используем предельный признак):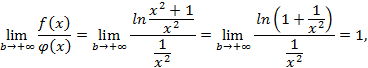
 сходится.
сходится. и имеет бесконечный разрыв при
и имеет бесконечный разрыв при  (рис.4). Если существует конечный предел
(рис.4). Если существует конечный предел 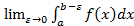 , то его называют несобственным интегралом второго рода.
, то его называют несобственным интегралом второго рода.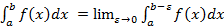 .
.
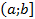 и имеет бесконечный разрыв в точке
и имеет бесконечный разрыв в точке 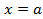 , то
, то 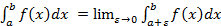 .
.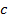 отрезка
отрезка 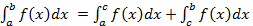 ,где
,где 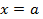 при
при 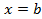 ,то необходимо сместиться в окрестности этих точек справа и слева соответственно.
,то необходимо сместиться в окрестности этих точек справа и слева соответственно.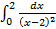 ; б)
; б) 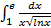 ; в)
; в) 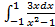 ; г)
; г) 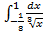 .
. разрывна в (·)
разрывна в (·) 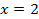 ,поэтому смещаемся в окрестность точки слева:
,поэтому смещаемся в окрестность точки слева: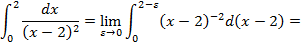
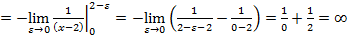 ,
,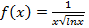 разрывна в (·)
разрывна в (·)  .В соответствии с правилом вычисления несобственных интегралов второго рода, имеем:
.В соответствии с правилом вычисления несобственных интегралов второго рода, имеем: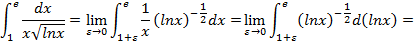
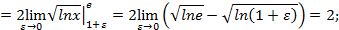
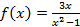 разрывна на концах интервала, то есть при
разрывна на концах интервала, то есть при 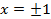 ,поэтому имеем:
,поэтому имеем: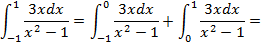
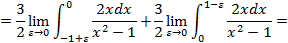
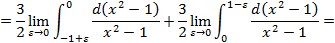
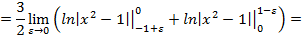
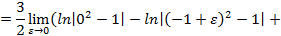
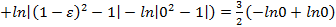 ,
,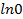 – не существует);
– не существует);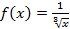 разрывна во внутренней (·)
разрывна во внутренней (·) 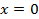 . Поэтому,
. Поэтому,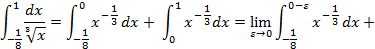
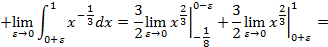
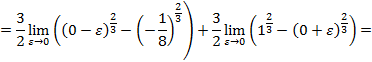
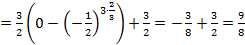 .
.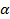 несобственный интеграл
несобственный интеграл 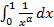 сходится и при каких расходится?
сходится и при каких расходится?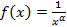 разрывна в (·)
разрывна в (·) 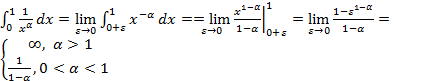 ;
;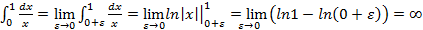 .
.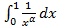 при
при 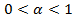 и расходится при
и расходится при 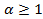 .
.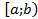 функции
функции 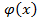 , при
, при 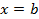 терпят бесконечный разрыв и удовлетворяют условию
терпят бесконечный разрыв и удовлетворяют условию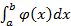 вытекает сходимость интеграла
вытекает сходимость интеграла 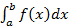 , а из расходимости интеграла
, а из расходимости интеграла 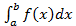 следует расходимость интеграла
следует расходимость интеграла 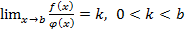 ,то интегралы
,то интегралы 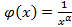 .В примере 4.12 показано, что несобственный интеграл
.В примере 4.12 показано, что несобственный интеграл 
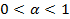 и расходится при
и расходится при 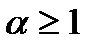 .
.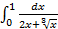 .;б)
.;б) 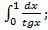 в)
в) 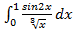 ;г)
;г) 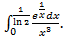
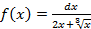 разрывна в точке
разрывна в точке 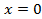 .Сравним ее с функцией
.Сравним ее с функцией  интеграл от которой
интеграл от которой 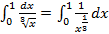 сходится, так как
сходится, так как 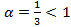 .Очевидна такая оценка на промежутке
.Очевидна такая оценка на промежутке 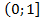 :
: 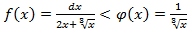 , следовательно, несобственный интеграл
, следовательно, несобственный интеграл  сходится (по признаку сравнения);
сходится (по признаку сравнения);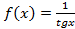 разрывна в точке
разрывна в точке 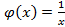 , интеграл от которой
, интеграл от которой 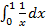 расходится, так как
расходится, так как 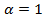 . А так как существует предел
. А так как существует предел 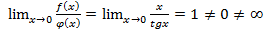 , то по предельному признаку интеграл
, то по предельному признаку интеграл 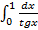 расходится.
расходится.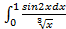 ;г)
;г) 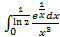 .
.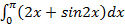 2.
2. 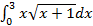 3.
3. 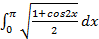 4.
4. 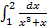 5.
5. 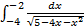 6.
6. 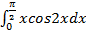 7.
7. 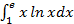 8.
8. 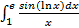 9.
9.  10.
10. 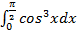
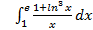
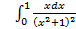
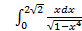
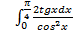
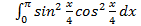
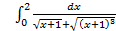
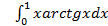
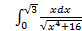
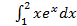
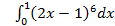
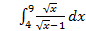
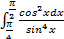
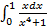
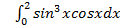
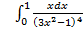
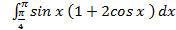
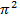 ; 10.2.
; 10.2. 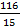 ; 10.3. 2; 10.4.
; 10.3. 2; 10.4. 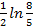 ; 10.5.
; 10.5. 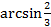 ; 10.6.
; 10.6. 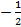 ; 10.7.
; 10.7. 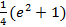 ; 10.8.
; 10.8. 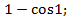 10.9.
10.9. 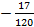 ;
; ; 10.11.
; 10.11. 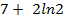 ; 10.12.
; 10.12.  ; 10.13.
; 10.13. 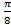 ; 10.14.
; 10.14. 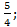
 ; 10.16.
; 10.16. 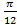 ; 10.17.
; 10.17. 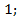 10.18.
10.18. 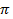 ; 10.19
; 10.19 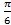 ; 10.20
; 10.20 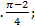
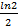 ; 10.22.
; 10.22. 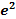 ; 10.23.
; 10.23.  ; 10.24.
; 10.24. 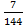 ;
;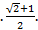
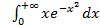
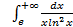
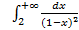
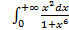
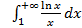
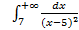
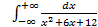
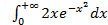
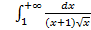
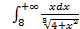
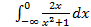
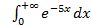
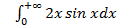
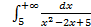
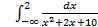
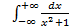
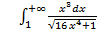
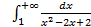
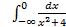
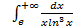
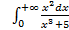
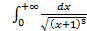
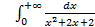
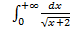
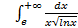
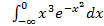
 ; 11.2. 1; 11.3. расходится; 11.4.
; 11.2. 1; 11.3. расходится; 11.4. 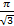 ; 11.5.
; 11.5.  ; 11.6. расходится; 11.7. расходится; 11.8.
; 11.6. расходится; 11.7. расходится; 11.8.  ; 11.9. расходится; 11.10.
; 11.9. расходится; 11.10. 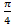 ; 11.11. расходится; 11.12.
; 11.11. расходится; 11.12. 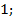 11.15.
11.15.  ; 11.17.
; 11.17. 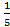 ; 11.20
; 11.20  11.21.
11.21. 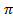 ; 11.22.
; 11.22. 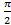 ; 11.23.
; 11.23.  ; 11.25. расходится; 11.26
; 11.25. расходится; 11.26 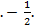
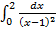 2.
2. 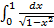 3.
3. 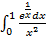
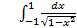
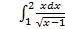
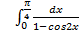
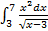
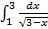
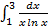
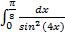
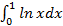
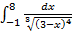
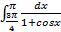
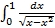
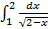
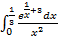
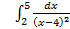
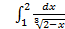
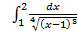
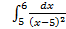
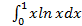
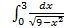
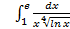
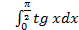
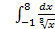
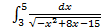
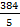 ;
;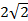 ; 12.6. расходится; 12.7. расходится; 12.8. -1;
; 12.6. расходится; 12.7. расходится; 12.8. -1; ; 12.16. расходится; 12.17. расходится; 12.18.
; 12.16. расходится; 12.17. расходится; 12.18.  ; 12.19
; 12.19 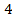 ; 12.20. расходится; 12.21.
; 12.20. расходится; 12.21. 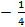 ; 12.22.
; 12.22.  ; 12.24. расходится; 12.25.
; 12.24. расходится; 12.25.  ; 12.26.
; 12.26. 


