
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
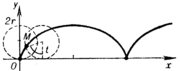
П. 4. Некоторые кривые, встречающиеся в математике и ее приложениях.
1. Лемниската Бернулли 2. Спираль Архимеда 3. Логарифмическая спираль 4. Циссоида Диокла 5. Кардиоида 6. Астроида 7. Циклоида
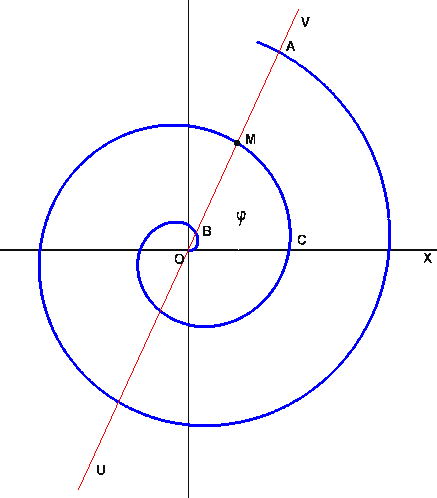
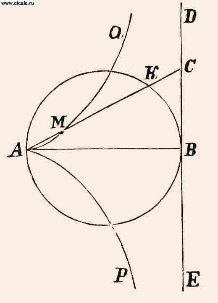
Спираль Архимеда Циссоиды
ветви циссоиды
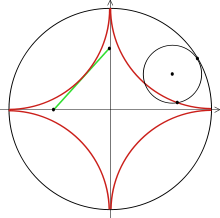
Кардиоида Астроида Циклоида
П. 5. Уравнения прямой на плоскости. 1. Общее уравнение прямой: где
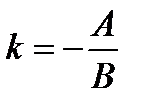 - угловой коэффициент - угловой коэффициент
2. Уравнение прямой, проходящей через данную точку
Вывод: Рассмотрим текущую (или произвольную) точку прямой 3. Уравнение прямой, проходящей через данную точку
Взаимное расположение двух прямых 1)
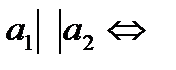 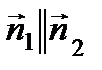 (координаты пропорциональны (координаты пропорциональны 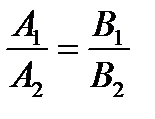 ) или ) или 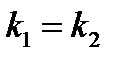 . .
2)
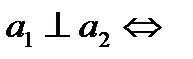 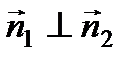 ( (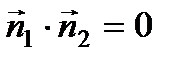 ) или ) или 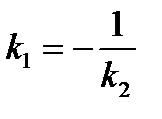 . .
3) Угол между прямыми
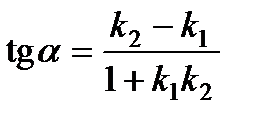
Точка пересечения прямых находится как:
4. Уравнение прямой, проходящей через две заданные точки
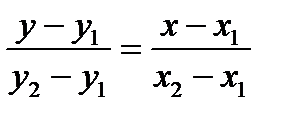 . (4) . (4)
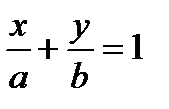 , (5) , (5)
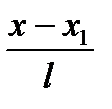 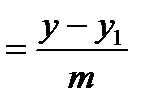 , (6) , (6)
т.е. уравнение прямой, проходящей через данную точку
7. Параметрические уравнения прямой т.е. уравнение прямой с параметром t, проходящей через данную точку Нормальное уравнение прямой
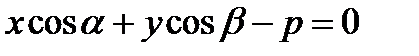 . (8) . (8)
Если положение прямой относительно осей координат определять длиной р перпендикуляра, опущенного из начала координат на прямую и углом α, образуемым этим перпендикуляром с положительным направлением оси (Ох). Общее уравнение прямой может быть приведено к нормальному уравнению путем умножения на нормирующий множитель Расстояние от точки М 0(х 0, у 0) до прямой
Чтобы найти расстояние от точки до прямой, нужно в нормальное уравнение прямой вместо текущих координат Пример 1. Дана прямая (а): 1) Составить уравнение прямой (а 1), проходящей через точку М 0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а 2), проходящей через точку М 0 (2, 1), перпендикулярно данной прямой. Решение. 1) 1 способ. Найдем угловой коэффициент прямой (а):
2 способ. Нормальный вектор 2) 1 способ. Найдем угловой коэффициент прямой (а):
2 способ. Нормальный вектор
Пример 2. Найти расстояние от прямой (АВ), где А (7, 4), В (3, –3) до точки С (5, 9). Решение. Найдем общее уравнение прямой. Для этого подставим исходные данные в формулу (4):
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.74.54 (0.015 с.) |
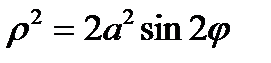 ,
, 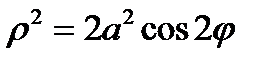
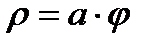
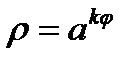 ,
, 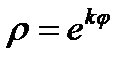
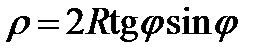 или
или 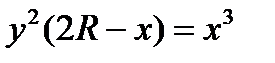
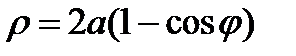 или
или 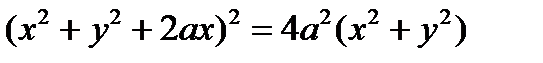
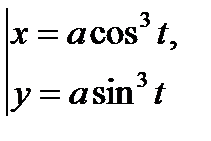 или
или 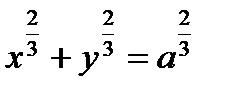
 или
или 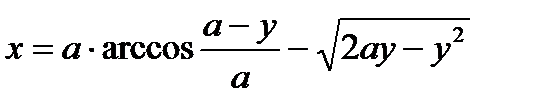
 или
или 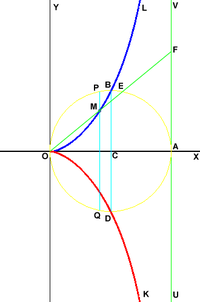 синяя и красная линии –
синяя и красная линии –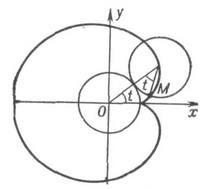
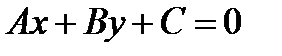 , (1)
, (1) 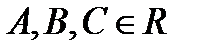 и
и 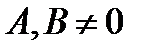 одновременно, т.к. в этом случае уравнение не будет содержать переменных и, следовательно, не будет выражать никакой зависимости между ними.
одновременно, т.к. в этом случае уравнение не будет содержать переменных и, следовательно, не будет выражать никакой зависимости между ними.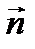
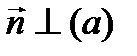 – нормальный вектор прямой.
– нормальный вектор прямой.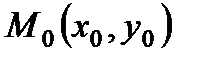 с заданным нормальным вектором
с заданным нормальным вектором 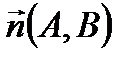 :
: 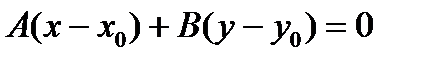 . (2)
. (2)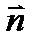
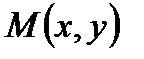 . Тогда вектор
. Тогда вектор 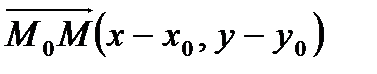 лежит на данной прямой. Следовательно, векторы
лежит на данной прямой. Следовательно, векторы 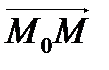 и
и  будут перпендикулярны:
будут перпендикулярны: 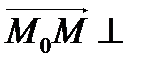
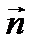 , то есть их скалярное произведение равно нулю
, то есть их скалярное произведение равно нулю 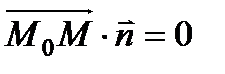 . Найдем скалярное произведение векторов, заданных своими декартовыми координатами:
. Найдем скалярное произведение векторов, заданных своими декартовыми координатами: 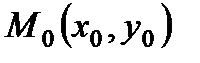 с заданным угловым коэффициентом k:
с заданным угловым коэффициентом k: 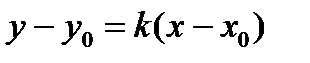 , (3)
, (3)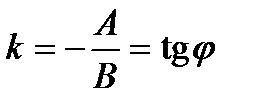 ,
,  угол между осью Ох (положительным направлением) и прямой.
угол между осью Ох (положительным направлением) и прямой.
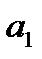
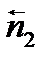
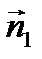
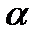
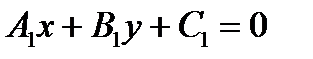 и
и 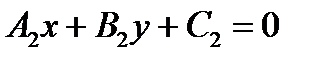
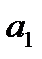
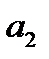
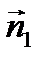
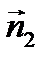
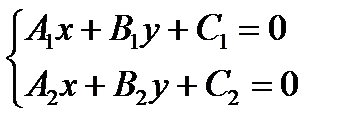
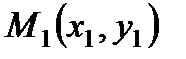 и
и 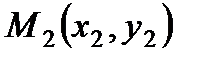 :
:

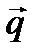
 параллельно заданному вектору
параллельно заданному вектору 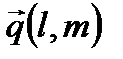 .
.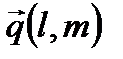 – направляющий вектор прямой.
– направляющий вектор прямой.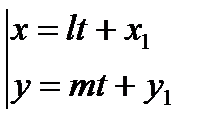 , (7)
, (7)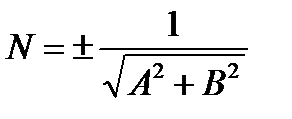 . Знак N выбирается противоположным к знаку С.
. Знак N выбирается противоположным к знаку С.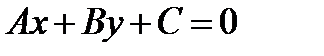
 М 0
М 0
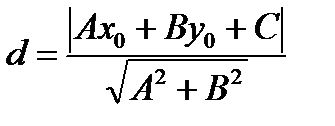 (9)
(9) подставить координаты точки
подставить координаты точки 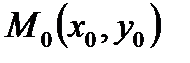 и взять абсолютную величину числа.
и взять абсолютную величину числа.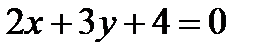 .
.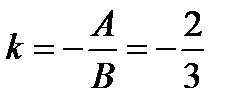 . Условие параллельности двух прямых:
. Условие параллельности двух прямых: 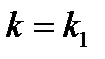 , то есть угловой коэффициент прямой (а 1):
, то есть угловой коэффициент прямой (а 1): 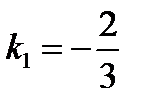 . Подставим в уравнение (3):
. Подставим в уравнение (3): 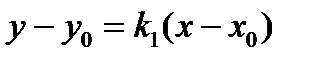 и получим
и получим 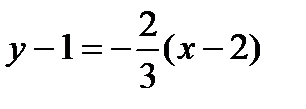 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: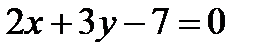 .
.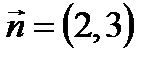 . Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а 1):
. Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а 1): 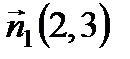 . Подставим в уравнение (2):
. Подставим в уравнение (2): 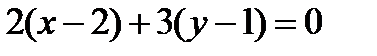 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: 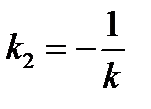 , то есть угловой коэффициент прямой (а 2):
, то есть угловой коэффициент прямой (а 2): 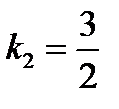 . Подставим в уравнение (3):
. Подставим в уравнение (3): 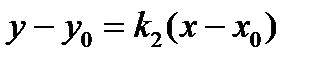 и получим
и получим 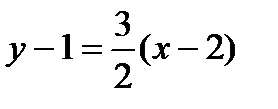 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: 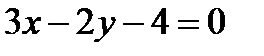 .
.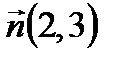 . Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а 2), то есть является направляющим вектором прямой (а 2):
. Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а 2), то есть является направляющим вектором прямой (а 2): 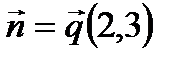 . Подставим в уравнение (4):
. Подставим в уравнение (4): 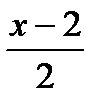
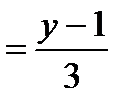 . Отсюда общее уравнение прямой (а 2) имеет вид:
. Отсюда общее уравнение прямой (а 2) имеет вид: 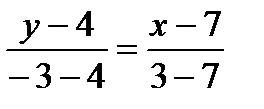 . Отсюда общее уравнение (АВ):
. Отсюда общее уравнение (АВ): 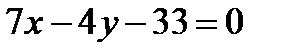 . По формуле (9)
. По формуле (9) 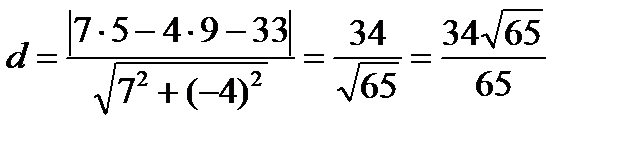 .
.


