
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Аналитическая геометрия.Стр 1 из 8Следующая ⇒
Глава 3. Аналитическая геометрия. Системы координат на плоскости. Понятие об уравнении линии на плоскости. П. 1. Декартовая система координат (ДСК)
Декартовая система координат (ДСК) на плоскости определяется заданием двух взаимно перпендикулярных лучей – осей (Ох) и (О y), одинаковой по обеим осям единицы масштаба и начала координат – точки О – точки пересечения осей.
Определение. Уравнение F (x, y) = 0 определяет на плоскости (Оху) некоторую линию l, представляющую собой геометрическое место точек, координаты которых удовлетворяют данному уравнению. И наоборот. Таким образом, линия задается уравнением между координатами, и обратно. Обычно уравнение разрешено относительно переменной y: y = f (x). Примеры линий: y = x – уравнение прямой, x 2 + y 2 = 9 – уравнение окружности.
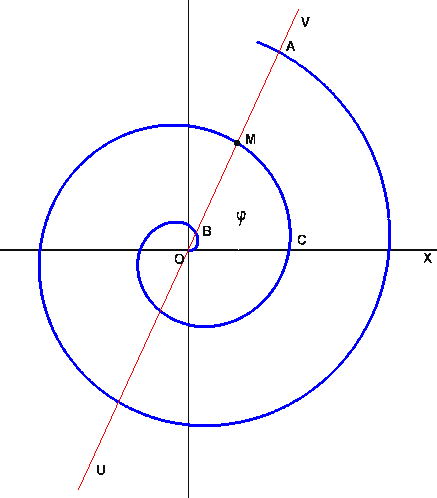
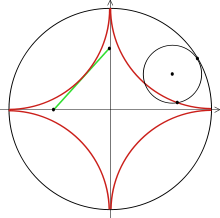
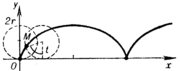
П. 4. Некоторые кривые, встречающиеся в математике и ее приложениях. 1. Лемниската Бернулли 2. Спираль Архимеда 3. Логарифмическая спираль 4. Циссоида Диокла 5. Кардиоида 6. Астроида 7. Циклоида
Спираль Архимеда Циссоиды
ветви циссоиды
Кардиоида Астроида Циклоида
П. 5. Уравнения прямой на плоскости. 1. Общее уравнение прямой: где
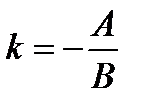 - угловой коэффициент - угловой коэффициент
2. Уравнение прямой, проходящей через данную точку
Вывод: Рассмотрим текущую (или произвольную) точку прямой
3. Уравнение прямой, проходящей через данную точку
Нормальное уравнение прямой
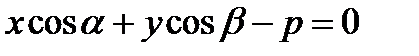 . (8) . (8)
Если положение прямой относительно осей координат определять длиной р перпендикуляра, опущенного из начала координат на прямую и углом α, образуемым этим перпендикуляром с положительным направлением оси (Ох). Общее уравнение прямой может быть приведено к нормальному уравнению путем умножения на нормирующий множитель Расстояние от точки М 0(х 0, у 0) до прямой
Чтобы найти расстояние от точки до прямой, нужно в нормальное уравнение прямой вместо текущих координат Пример 1. Дана прямая (а): 1) Составить уравнение прямой (а 1), проходящей через точку М 0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а 2), проходящей через точку М 0 (2, 1), перпендикулярно данной прямой. Решение. 1) 1 способ. Найдем угловой коэффициент прямой (а):
2 способ. Нормальный вектор 2) 1 способ. Найдем угловой коэффициент прямой (а):
2 способ. Нормальный вектор
Пример 2. Найти расстояние от прямой (АВ), где А (7, 4), В (3, –3) до точки С (5, 9). Решение. Найдем общее уравнение прямой. Для этого подставим исходные данные в формулу (4): 1. Окружность Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Окружность радиуса R с центром в точке
Любое уравнение окружности с помощью тождественных преобразований можно привести к каноническому виду (1). Для этого достаточно выделить полные квадраты по переменным x и у. Пример. Постройте кривую Решение. Сгруппируем Выделим полные квадраты, получим:
Тогда каноническое уравнение имеет вид: Итак, центр окружности – точка М 0(1,-3), радиус равен 2.
Эллипс Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек
Рис.2
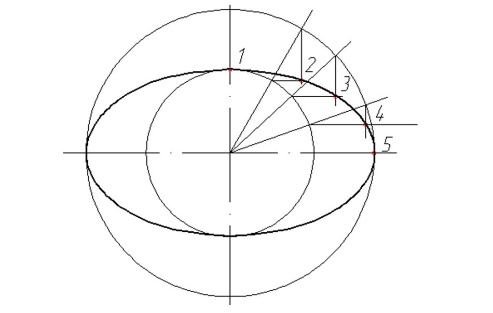
Координаты фокусов F 1(-с,0), F 2(с,0), тогда расстояние между фокусамиравно 2 с: | F 1 F 2|=2 c, В выбранной системе координат эллипс имеет каноническое уравнение Свойства эллипса. Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (2), то его осями симметрии служат оси Ox и Оу, начало координат – центр симметрии. Построение эллипса. Строим две окружности с центром в точке О радиусами а и b (a > b). Строим луч, выходящий из начала координат до пересечения с обеими окружностями. Из точек пересечения опускаем пересекающиеся лучи, параллельные координатным осям. Точка пересечения данных лучей – это точка, принадлежащая эллипсу (рис.3).
Рис.3 Определения. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии - центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины – большой полуосью эллипса. Если эллипс задан каноническим уравнением Величина
Прямые Замечание 1. Уравнение (2) было получено в предположении, что Замечание 2. Если Замечание 3. Если центр эллипса лежит в точке Пример 1. Постройте кривую
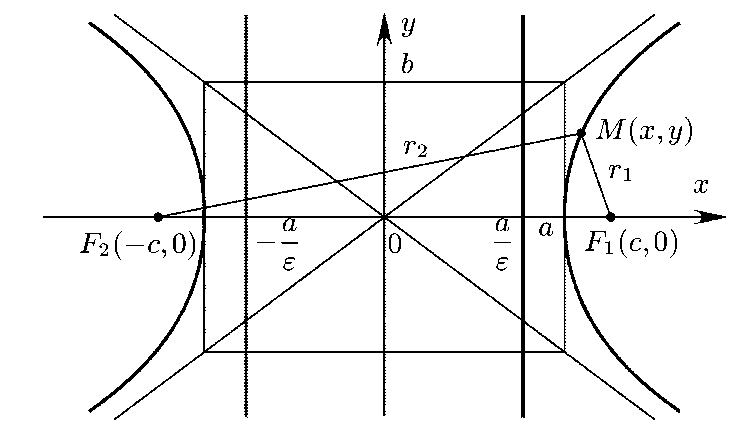
Рис.4 Пример 2. Найдите фокусы и эксцентриситет эллипса Решение. Уравнение запишем в виде Гипербола. Из школьного курса математики известно, что кривая, задаваемая уравнением Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек F 1 и F 2 той же плоскости, называемых фокусами гиперболы, есть величина постоянная, меньшая, чем расстояние между фокусами и равная 2 а. Пусть расстояние между фокусами гиперболы равно 2 c, т.е. фокусы имеют координаты
Рис.5
тогда каноническое уравнение гиперболы имеет вид:
где Свойство. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением (3), то ее осями симметрии служат координатные оси Ox и Оу, а начало координат - центр симметрии гиперболы (рис.5). Определения. Точки пересечения гиперболы, заданной каноническим уравнением (3), с осью Ox называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0, - b) и (0, b) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина Прямые Построение гиперболы. Чертим основной прямоугольник, т.е. прямоугольник с центром в начале координат со сторонами 2 a и 2 b, диагоналями которого будут асимптотами гиперболы (см. рис. выше в определении).
Замечание 2. Если каноническое уравнение гиперболы имеет вид
Рис.6 то ее фокусы располагаются на оси Оу, их координаты F 1(0,- с), F 2(0, с), числа a и b называются соответственно мнимой и действительной полуосями гиперболы; уравнения асимптот Замечание 3. Если центр гиперболы смещен и лежит в точке
Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение Рис.7 Пример 2. Постройте гиперболу Решение. Преобразуем уравнение к виду
Асимптоты имеют уравнение Рис.8 Парабола
Пусть расстояние между фокусом Рис.9
Замечание. Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью Ox. Асимптот парабола не имеет. Определение. Точка пересечения оси симметрии с параболой называется вершиной параболы. П. 4. Уравнение плоскости
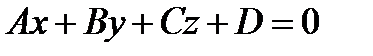 (1) (1)
Координаты нормального вектора: Уравнение плоскости, проходящей через данную точку
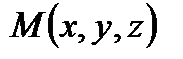 и рассмотрим вектор и рассмотрим вектор 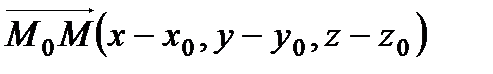 , который будет лежать в плоскости α. Нормальный вектор , который будет лежать в плоскости α. Нормальный вектор 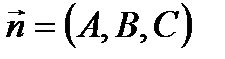 перпендикулярен плоскости α, следовательно, векторы перпендикулярен плоскости α, следовательно, векторы 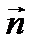 и и 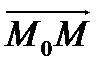 перпендикулярны. Условие перпендикулярности векторов – равенство нулю их скалярного произведения: перпендикулярны. Условие перпендикулярности векторов – равенство нулю их скалярного произведения: 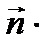  =0, то есть =0, то есть
 . .
Уравнение плоскости в отрезках где a, b, c – величины отрезков, отсекаемых плоскостью на координатных осях с точностью до знака. П. 5. Прямая в пространстве Рассмотрим в пространстве R 3 прямую (а), проходящую через данную точку
Вывод уравнения (а): Рассмотрим текущую точку прямой
Уравнение прямой, проходящей через две заданные точки Вывод: Рассмотрим текущую точку прямой
Приравняем уравнение (2) к параметру t:
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей:
 , координаты точки M 0(x 0, y 0 z 0), лежащей на прямой, удовлетворяют системе уравнений (4). , координаты точки M 0(x 0, y 0 z 0), лежащей на прямой, удовлетворяют системе уравнений (4).
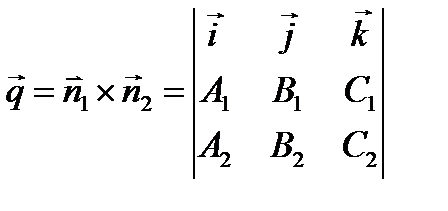
Примеры.
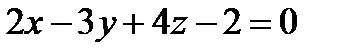 , проходящей через точку М0 (0, 0, 1/2). , проходящей через точку М0 (0, 0, 1/2).
Нормальный вектор плоскости коллинеарен направляющему вектору прямой вектора прямой пропорциональны (совпадают) с координатами нормального вектора. Подставим данные в каноническое уравнение: Ответ: Задача 2. Найти точку пересечения прямой Решение. Координаты точки пересечения М – это решение системы Запишем уравнение прямой в параметрическом виде:
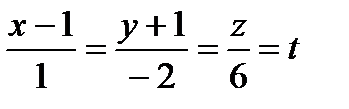 , отсюда , отсюда 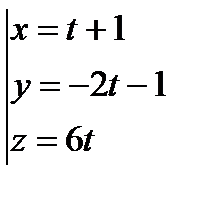 . .
Найдем решение системы:
отсюда х = 1+1=2, у = -2 - 1= -3, z = 6 – координаты точки пересечения. Ответ: Задача 3. Найти угол Решение.
Задача 4. Написать уравнение проекции прямой l: Решение.
 , , 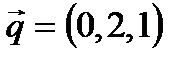 . .
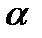 , ,
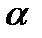 . .
Пересечение полученной плоскости с плоскостью прямая d - и будет искомой проекцией. Уравнение плоскости Тогда общее уравнение искомой прямой d имеет вид: Запишем это уравнение в каноническом виде. Для этого необходимо найти точку А, лежащую на прямой, и направляющий вектор Найдем координаты точки А: пусть z = 0, тогда х = 0, у =-1. Координаты точки А (0, -1, 0). Направляющий вектор Уравнение прямой d – уравнение искомой проекции имеет вид: Вывод. Определение. Сфера – геометрическое место точек, расстояние от которых до данной точки М 0(х 0, у 0, z 0) – центра есть величина постоянная и равная R. Рассмотрим текущую точку сферы М (х, у, z). Тогда Цилиндрические поверхности
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.115 (0.15 с.) |
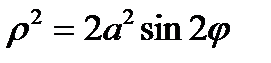 ,
, 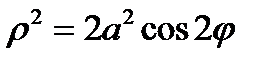
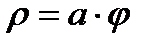
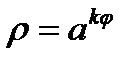 ,
, 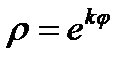
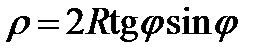 или
или 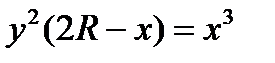
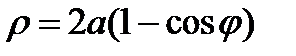 или
или 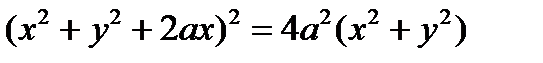
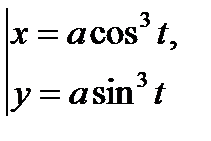 или
или 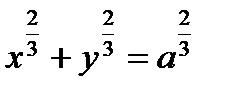
 или
или 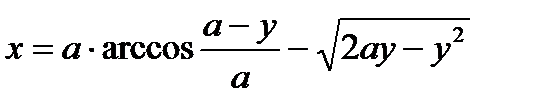
 или
или  синяя и красная линии –
синяя и красная линии –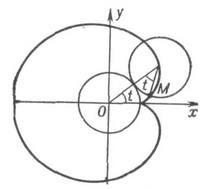
 , (1)
, (1) 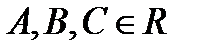 и
и 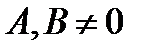 одновременно, т.к. в этом случае уравнение не будет содержать переменных и, следовательно, не будет выражать никакой зависимости между ними.
одновременно, т.к. в этом случае уравнение не будет содержать переменных и, следовательно, не будет выражать никакой зависимости между ними.
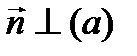 – нормальный вектор прямой.
– нормальный вектор прямой.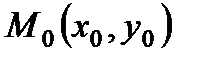 с заданным нормальным вектором
с заданным нормальным вектором 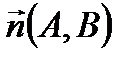 :
: 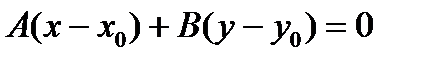 . (2)
. (2)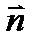
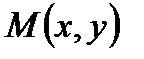 . Тогда вектор
. Тогда вектор 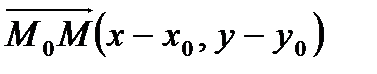 лежит на данной прямой. Следовательно, векторы
лежит на данной прямой. Следовательно, векторы 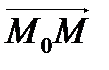 и
и  будут перпендикулярны:
будут перпендикулярны: 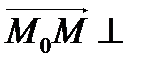
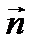 , то есть их скалярное произведение равно нулю
, то есть их скалярное произведение равно нулю 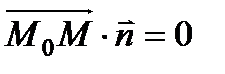 . Найдем скалярное произведение векторов, заданных своими декартовыми координатами:
. Найдем скалярное произведение векторов, заданных своими декартовыми координатами: 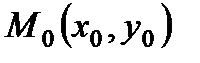 с заданным угловым коэффициентом k:
с заданным угловым коэффициентом k: 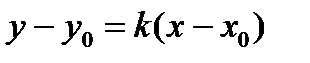 , (3)
, (3)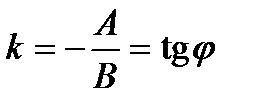 ,
,  угол между осью Ох (положительным направлением) и прямой.
угол между осью Ох (положительным направлением) и прямой.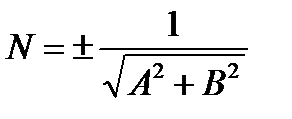 . Знак N выбирается противоположным к знаку С.
. Знак N выбирается противоположным к знаку С.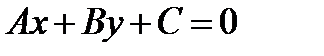
 М 0
М 0
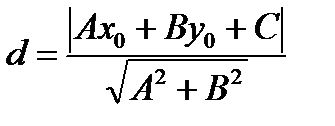 (9)
(9) подставить координаты точки
подставить координаты точки 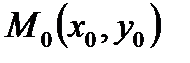 и взять абсолютную величину числа.
и взять абсолютную величину числа.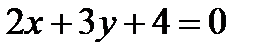 .
.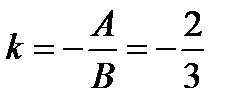 . Условие параллельности двух прямых:
. Условие параллельности двух прямых: 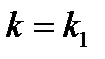 , то есть угловой коэффициент прямой (а 1):
, то есть угловой коэффициент прямой (а 1): 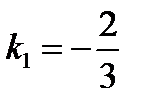 . Подставим в уравнение (3):
. Подставим в уравнение (3): 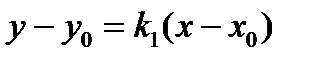 и получим
и получим 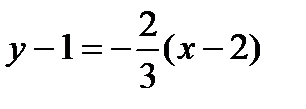 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: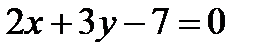 .
.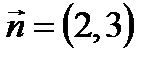 . Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а 1):
. Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а 1): 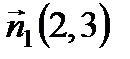 . Подставим в уравнение (2):
. Подставим в уравнение (2): 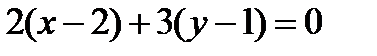 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: 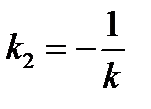 , то есть угловой коэффициент прямой (а 2):
, то есть угловой коэффициент прямой (а 2): 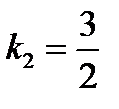 . Подставим в уравнение (3):
. Подставим в уравнение (3): 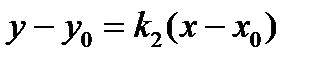 и получим
и получим 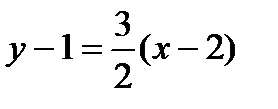 . Отсюда общее уравнение прямой (а 1) имеет вид:
. Отсюда общее уравнение прямой (а 1) имеет вид: 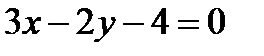 .
.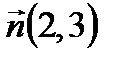 . Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а 2), то есть является направляющим вектором прямой (а 2):
. Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а 2), то есть является направляющим вектором прямой (а 2): 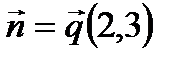 . Подставим в уравнение (4):
. Подставим в уравнение (4): 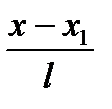
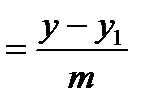 и получим
и получим 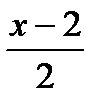
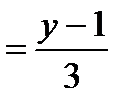 . Отсюда общее уравнение прямой (а 2) имеет вид:
. Отсюда общее уравнение прямой (а 2) имеет вид: 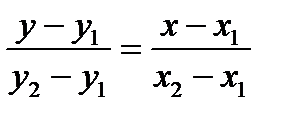 и получим
и получим 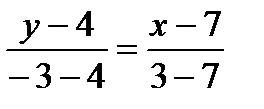 . Отсюда общее уравнение (АВ):
. Отсюда общее уравнение (АВ): 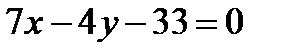 . По формуле (9)
. По формуле (9) 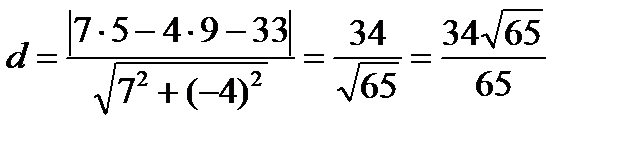 .
.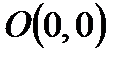 задается уравнением
задается уравнением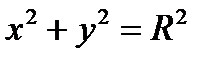
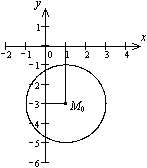 Окружность радиуса R с центром в точке
Окружность радиуса R с центром в точке 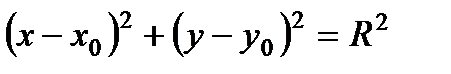 (1)
(1)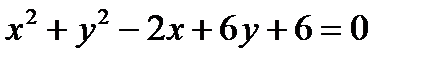 .
.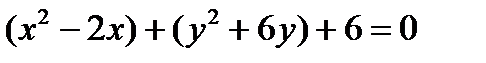 .
.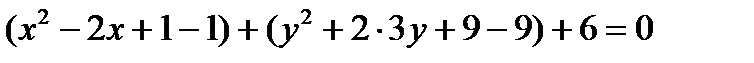 .
.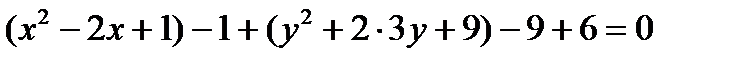 ,
,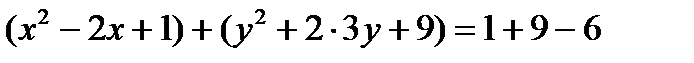 .
.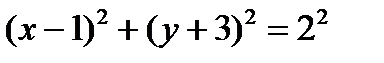 .
. 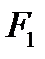 и
и 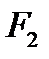 той же плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами и равная 2 а.
той же плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами и равная 2 а.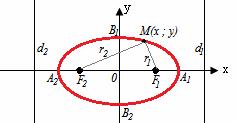
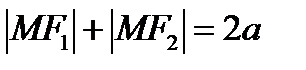 .
.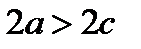 .
.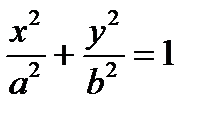 (2),
(2),
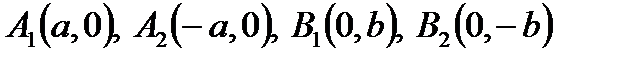 , большая полуось равна a, малая полуось равна b.
, большая полуось равна a, малая полуось равна b.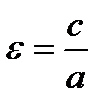 , где
, где 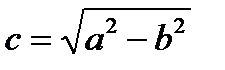 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 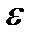 эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса
эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 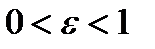 .
. 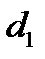 и
и 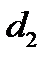 , между которыми вытянут эллипс, называются директрисами, уравнения которых
, между которыми вытянут эллипс, называются директрисами, уравнения которых 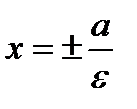 .
.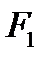 и
и 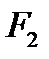 – различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением, можем рассмотреть и в случае
– различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением, можем рассмотреть и в случае 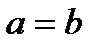 ,
, 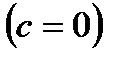 . Уравнение в этом случае после умножения на
. Уравнение в этом случае после умножения на 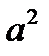 примет вид
примет вид  . Это уравнение окружности радиуса
. Это уравнение окружности радиуса  с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда
с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда 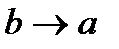 ,
, 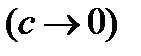 , или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.
, или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.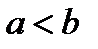 , то фокусы лежат на оси Оу и имеют координаты F 1(0,- с), F 2(0, с), где
, то фокусы лежат на оси Оу и имеют координаты F 1(0,- с), F 2(0, с), где 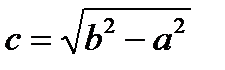 . Эксцентриситет
. Эксцентриситет 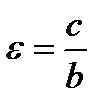 . Уравнения директрис
. Уравнения директрис 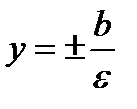
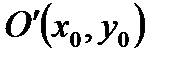 , то каноническое уравнение эллипса примет вид:
, то каноническое уравнение эллипса примет вид: 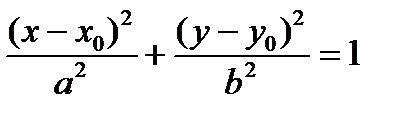 . Уравнения директрис
. Уравнения директрис 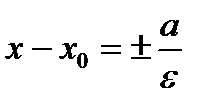 , координаты фокусов F 1(х 0– с, у 0), F 2((х 0+ с, у 0).
, координаты фокусов F 1(х 0– с, у 0), F 2((х 0+ с, у 0).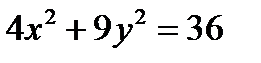 . Найдите фокусы и эксцентриситет.
. Найдите фокусы и эксцентриситет.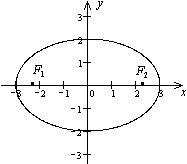 Решение. Разделим обе части уравнения на 36. Получаем уравнение
Решение. Разделим обе части уравнения на 36. Получаем уравнение 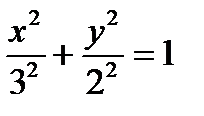 . Это каноническое уравнение эллипса,
. Это каноническое уравнение эллипса, 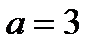 ,
, 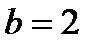 . Из соотношения находим
. Из соотношения находим 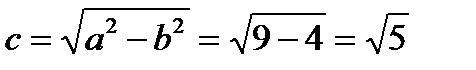 , фокусы F 1(
, фокусы F 1(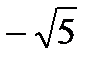 , 0), F 2(
, 0), F 2(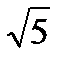 , 0), эксцентриситет
, 0), эксцентриситет 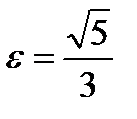 .
.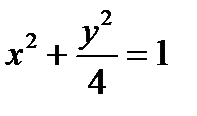 .
.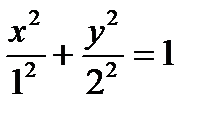 , где
, где 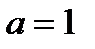 ,
, 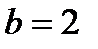 , b > a. Отсюда
, b > a. Отсюда 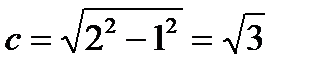 . Фокусы имеют координаты F 1(
. Фокусы имеют координаты F 1(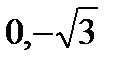 ), F 2(
), F 2(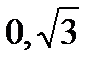 ). Эксцентриситет равен
). Эксцентриситет равен 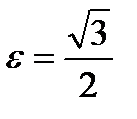 .
. 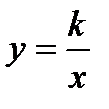 , где
, где 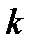 – число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола).
– число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола).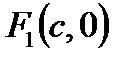 и
и 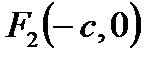 ,
, 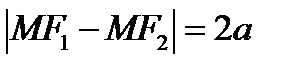 ,
, 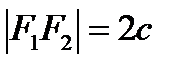 ,
, 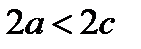 ,
,
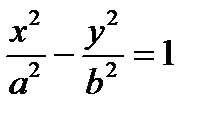 (3),
(3),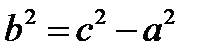 или
или 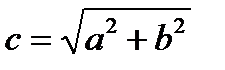 .
.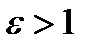 . Эксцентриситет характеризует угол между асимптотами, чем ближе
. Эксцентриситет характеризует угол между асимптотами, чем ближе 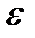 к 1, тем меньше этот угол.
к 1, тем меньше этот угол.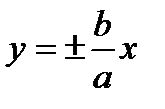 , к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис
, к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис 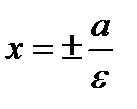 (рис.5).
(рис.5).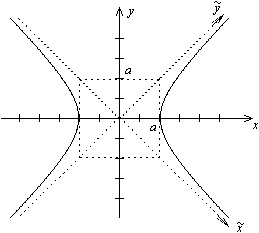 Замечание 1. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами a и b может быть произвольным. В частности, при
Замечание 1. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами a и b может быть произвольным. В частности, при 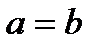 мы получим равностороннюю гиперболу (рис.6).
мы получим равностороннюю гиперболу (рис.6).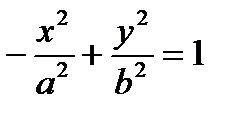 (3*),
(3*),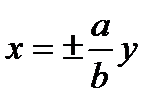 , уравнения директрис
, уравнения директрис 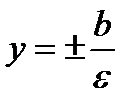 . (См. рис.8)
. (См. рис.8)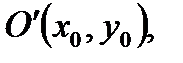 то каноническое уравнение гиперболы примет вид:
то каноническое уравнение гиперболы примет вид: 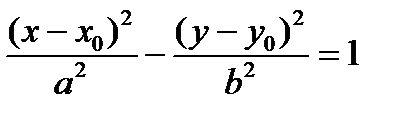 (или
(или 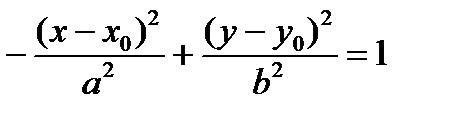 ). Тогда координаты фокусов F 1(х 0- с, у 0), F 2(х 0+ с, у 0), уравнения асимптот
). Тогда координаты фокусов F 1(х 0- с, у 0), F 2(х 0+ с, у 0), уравнения асимптот 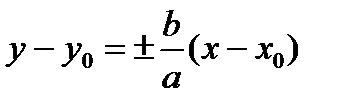 , уравнения директрис
, уравнения директрис 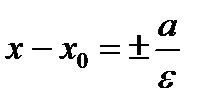 .
.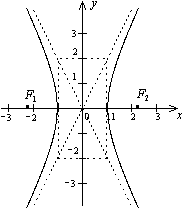 Пример 1. Постройте гиперболу
Пример 1. Постройте гиперболу  , найдите ее фокусы и эксцентриситет.
, найдите ее фокусы и эксцентриситет.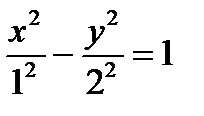 ,
, 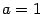 ,
, 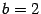 . Проводим асимптоты
. Проводим асимптоты 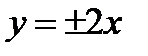 и строим гиперболу. Из формулы получим
и строим гиперболу. Из формулы получим 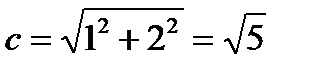 . Тогда фокусы
. Тогда фокусы 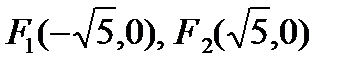 , эксцентриситет
, эксцентриситет  (рис.7).
(рис.7). 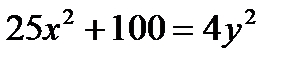 . Найдите ее фокусы и эксцентриситет.
. Найдите ее фокусы и эксцентриситет.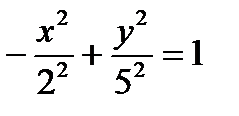 . Фокусы гиперболы лежат на оси (Оу), действительная полуось
. Фокусы гиперболы лежат на оси (Оу), действительная полуось 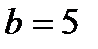 , мнимая
, мнимая 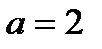 .
. 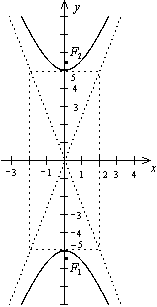
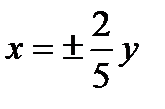 . Из формулы получим
. Из формулы получим 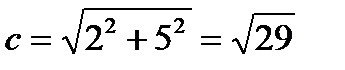 , эксцентриситет
, эксцентриситет 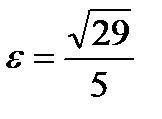 , координаты фокусов
, координаты фокусов 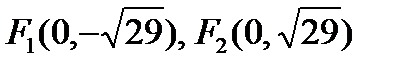 (рис.8)
(рис.8)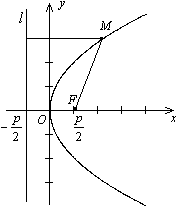 Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.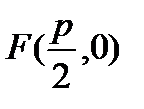 и директрисой параболы l, уравнение которой
и директрисой параболы l, уравнение которой 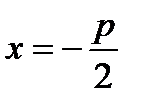 , равно p (
, равно p (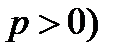 . Тогда каноническое уравнение параболы имеет вид:
. Тогда каноническое уравнение параболы имеет вид: 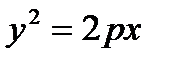 . (4)
. (4)
 ,
, 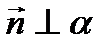 .
.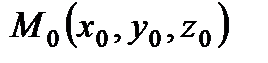 , перпендикулярно заданному вектору
, перпендикулярно заданному вектору 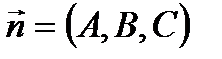 :
: 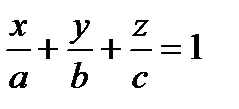 , (3)
, (3) , параллельно заданному вектору
, параллельно заданному вектору  . Вектор
. Вектор 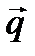
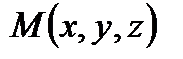 и рассмотрим вектор
и рассмотрим вектор 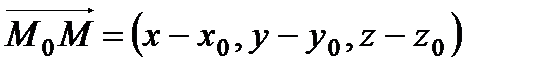 , который будет лежать на прямой (а). Направляющий вектор прямой
, который будет лежать на прямой (а). Направляющий вектор прямой  и
и 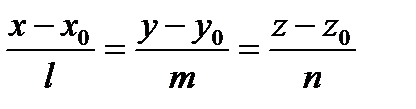 – канонические уравнения прямой. (1)
– канонические уравнения прямой. (1)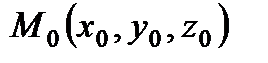 и
и 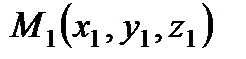
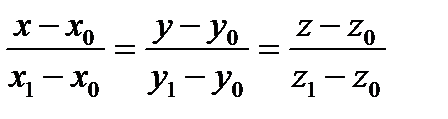 (2)
(2)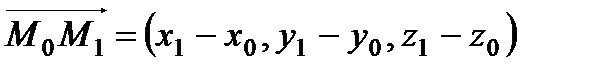 , которые будут параллельны. Условие коллинеарности двух векторов – пропорциональность их координат.
, которые будут параллельны. Условие коллинеарности двух векторов – пропорциональность их координат.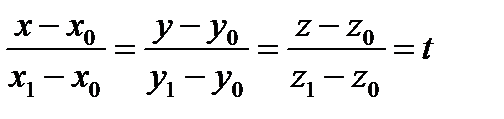 , отсюда
, отсюда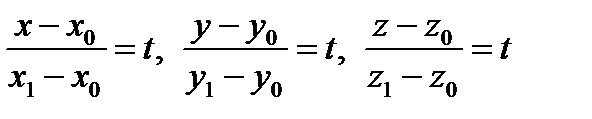 или
или  – параметрические уравнения прямой (3)
– параметрические уравнения прямой (3)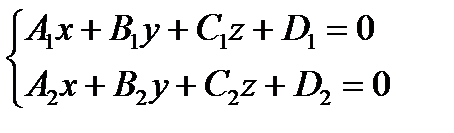 – общие уравнения прямой (4).
– общие уравнения прямой (4).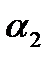
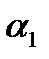
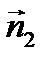



 α
α
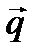
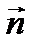
 . Следовательно, координаты направляющего
. Следовательно, координаты направляющего
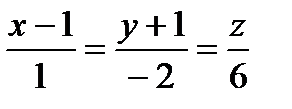 и плоскости
и плоскости 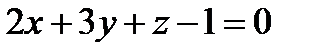 .
.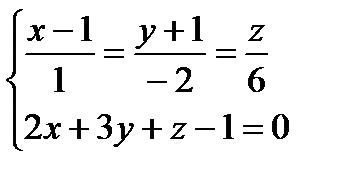 .
.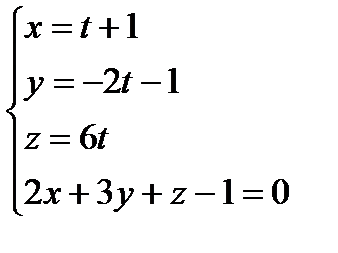
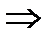
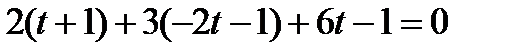
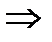
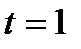 ,
,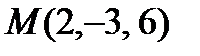 .
. между прямой в:
между прямой в:  и плоскостью
и плоскостью  .
. ,
, 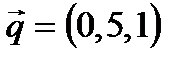 . Угол между прямой и плоскостью находится по формуле:
. Угол между прямой и плоскостью находится по формуле: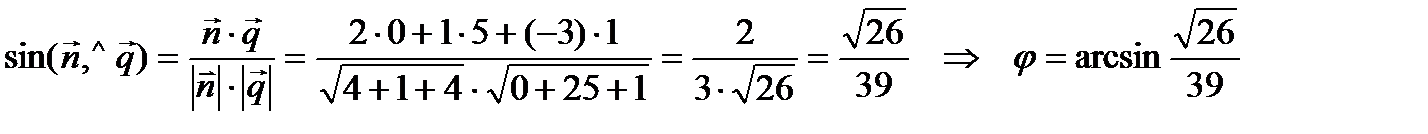 .
.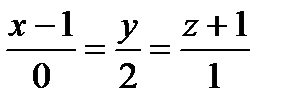 на плоскость
на плоскость 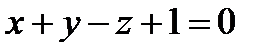 .
. α
α
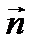
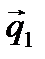 А
А
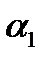 , походящей через прямую l перпендикулярно плоскости
, походящей через прямую l перпендикулярно плоскости  . Нормальный вектор
. Нормальный вектор  .
.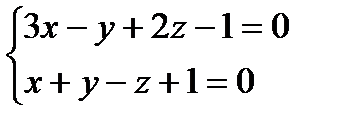 .
. 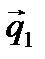 .
.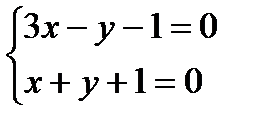 , методом Гаусса получим, что
, методом Гаусса получим, что найдем по формуле:
найдем по формуле: 
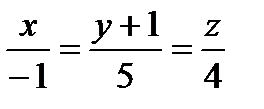 .
.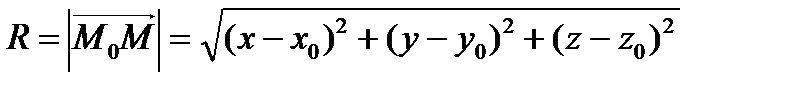 . Отсюда
. Отсюда 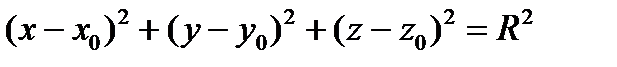 – каноническое уравнение сферы с центром в точке М 0(х 0, у 0, z 0) и радиусом R.
– каноническое уравнение сферы с центром в точке М 0(х 0, у 0, z 0) и радиусом R.


