
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональные на промежутке системы функций
Если То
Если нормы всех ф-ий системы (1) равны единицы, то это система называется ортонормированной. Для ортонормированных систем
Чтобы любую систему, не содержащую функцийй с нулевой нормой, пронормировать, необходимо каждую функцию разделить на ее норму:
Если система ф-ий
Имеют вид:
Обобщенный полином с коэффициентом Фурье данной ф-ии обладает наименьшим квадратичным отклонением от этой ф-ии по сравнению со всеми другими обобщенными полиномами того же порядка m.
После преобразований (раскрывая скобки, меняя местами
Из (3) следует, что
(7)
Если система Если Для полной ортонормированной системы имеет место равенство Парсеваля
1. при увеличении числа слагаемых m младшие коэффициенты 2. при увеличении m квадратичная погрешность
4.2. Основные понятия гармонического анализа. Тригонометрическая система функций: 1, sin x, cos x, sin 2x, cos 2x,…, sin nx, cos nx (1) ортогональна на любом отрезке длины 2π (напрмер, на [-π, π]). Нормы функций системы (1)
Пусть дана непрерывная периодическая функция с периодом 2π (введением новой переменной можно область определения функции [a, b] перевести в интервал [-π,π]) Составим тригонометрический полином
Слагаемые Чтобы минимизировать
Коэффициенты т.е.
Т.о. получаем:
(k=0,1,2,…m) Полином (3) – тригонометрический полином Фурье;
Если f(х) четная, то
Если f(х) нечетная, то
Для четной функции - При m→∞ получаем тригонометрический ряд Фурье
В простейших случаях коэффициенты тригонометрического полинома Фурье вычисляются непосредственно по формулам (4) Среднеквадратическое отклонение
в общем случае функция
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.78.106 (0.007 с.) |
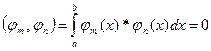 , при m<>n,
, при m<>n,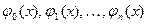 - система ф-ий, ортогональных (1) на [a,b]
- система ф-ий, ортогональных (1) на [a,b]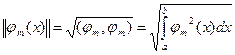 - норма ф-ий
- норма ф-ий 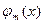 на [a,b]
на [a,b]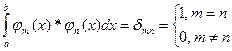
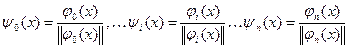
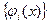 ортогональна на отрезке [a,b], то коэффициенты
ортогональна на отрезке [a,b], то коэффициенты 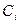 обобщенного полинома
обобщенного полинома 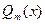
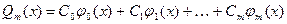 , аппроксимирующего непрерывную ф-ию f(x)на [a,b]
, аппроксимирующего непрерывную ф-ию f(x)на [a,b]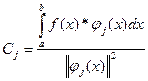

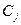 -коэфф. Фурье ф-ии f(x) относительно заданной ортогональной системы
-коэфф. Фурье ф-ии f(x) относительно заданной ортогональной системы 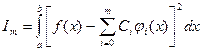 (3)
(3) и
и  и приводя подобные члены) получим(без вывода):
и приводя подобные члены) получим(без вывода):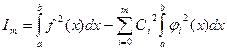 (4)
(4)
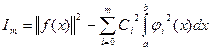 (5)
(5) 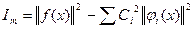
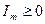 , потому из (5) получаем:
, потому из (5) получаем: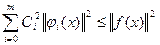 (6) –неравенство Бесселя
(6) –неравенство Бесселя При m ∞
При m ∞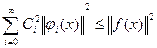
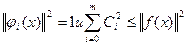 (8)
(8)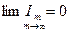 , то система
, то система 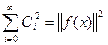 (9)
(9) с коэффициентами Фурье:
с коэффициентами Фурье: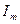 монотонно убывает в широком смысле, т.е.
монотонно убывает в широком смысле, т.е. 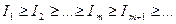 Т.о. присоединение новых слагаемых увеличивает точность аппроксимации.
Т.о. присоединение новых слагаемых увеличивает точность аппроксимации.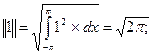
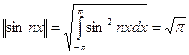
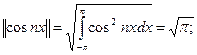 n=1,2…. (2)
n=1,2…. (2)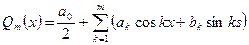 (3)
(3)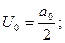
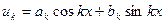 k=1,2…, называются гармонитами.
k=1,2…, называются гармонитами.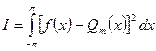
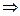 min
min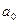 ,
, 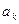 ,
, 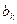 должны быть коэффициентами Фурье функции f(х) относительно системы (1)
должны быть коэффициентами Фурье функции f(х) относительно системы (1)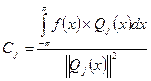
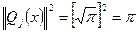
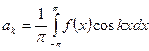
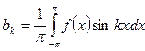 (4)
(4)
 (k=1,2,…,m)
(k=1,2,…,m) 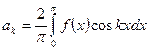 k=0,1,2…m (5)
k=0,1,2…m (5) 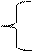
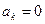 (k=0,1,2,…,m)
(k=0,1,2,…,m)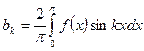 (k=1,2,…,m) (6)
(k=1,2,…,m) (6)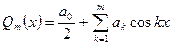
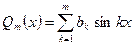
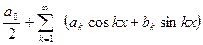

 Представленные функции тригонометрическим полиномом Фурье или тригонометрическим рядом Фурье называется гармоническим анализом.
Представленные функции тригонометрическим полиномом Фурье или тригонометрическим рядом Фурье называется гармоническим анализом.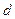 определено как
определено как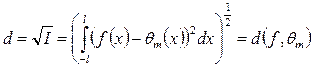 ,
,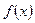 задана на интервале
задана на интервале 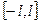 .
.


