
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
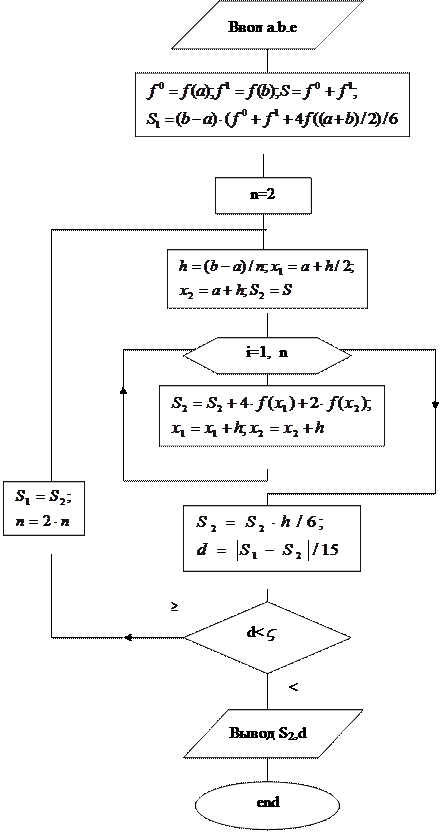
Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.
ЛЕКЦИЯ 13 Численное интегрирование (продолжение) Квадратурные формулы Гаусса Пусть отрезок интегрирования На каждом из интервалов а) б) Определенный интеграл от функции
Так чтобы для выбранной степени р сплайна построить квадратурные формулы Гаусса, необходимо найти из условий а) и б) 2m неизвестных: m неизвестных коэффициентов m координат узлов Будем решать задачу одновременно для всех участков
Тогда: И при
Положим:
Тогда:
и (1) примет вид:
Теперь рассмотрим квадратную формулу Гаусса с тремя узлами (m=3). При этом необходимо определить шесть величин: Функция
Подставим (3) в (2). Учитывая, что В общем случае степень аппроксимирующего полинома равна: p=2m-1, где m-число узлов. Для трех узлов имеем р=5, т.е. многочлен пятой степени. Коэффициенты при
Приравнивая коэффициенты при
Решение системы (6) – нелинейной системы найти очень сложно! Однако оказывается, что неизвестное
Нули многочлена (7) принадлежат интервалу В нашем случае m=3:
т.о. Корни (нули) уравнения
Т.о. найдены значения Значения
Решение системы:
Подставим найденные значения в (1):
Т.о. Для
Т.о.
Итак, квадратичная формула Гаусса с тремя узлами имеет вид:
Где Если
При вычислении интеграла до достижения заданной точки Е методом двойного перечета, условие окончаний вычисления имеет вид:
Где k=2m, m-число узлов. При этом полагают, что
Пример: Найти приближенное значение интеграла Оценить погрешность вычислений. Решение. Ищем:
R(h) а ≤ х ≤ в С погрешностью не больше чем 0,0019<0,002 имеем
Здесь х2 = 0,5; f(x2) = 1.284025 x1 = x2 - x3 = x2 -
Для достижения точности того же порядка с использованием: формулы Симпсона n=2 (ε=0,0045) формулы прямоугольников n=10 (0,0068)
ЛЕКЦИЯ 14
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.109 (0.008 с.) |
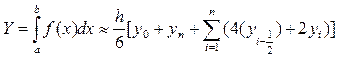
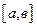 непрерывной функции f(x) разбит на n равных частей точками
непрерывной функции f(x) разбит на n равных частей точками 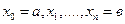 . Шаг разбиения
. Шаг разбиения  . Пусть
. Пусть 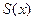 - функция аппроксимирующая подынтегральная функцию f(x).
- функция аппроксимирующая подынтегральная функцию f(x).
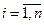 расположено m узлов
расположено m узлов 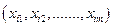 , в которых
, в которых  . Пусть
. Пусть  - многочлен степени р, такой что
- многочлен степени р, такой что 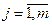
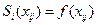
 в узлах в виде их линейной комбинации т.е.
в узлах в виде их линейной комбинации т.е. (1)
(1)
 (
(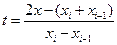
 , и
, и 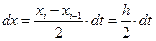

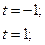 т.о.
т.о. 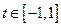
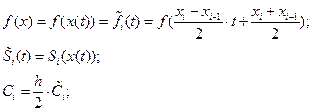

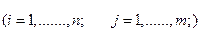
 (2)
(2)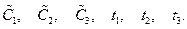
 -многочлен степени р.
-многочлен степени р. (3)
(3) получим тождество относительно коэффициентов
получим тождество относительно коэффициентов 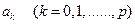

 (5)
(5)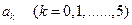 в правой и левых частях и учитывая (5), получим шесть уравнений:
в правой и левых частях и учитывая (5), получим шесть уравнений: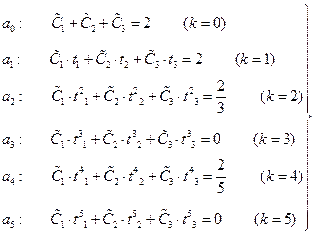 (6)
(6)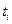 в уравнениях (6) совпадают с нулями многочлена Лежандра:
в уравнениях (6) совпадают с нулями многочлена Лежандра: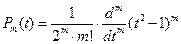 (7)
(7) и расположены симметрично середины интервала.
и расположены симметрично середины интервала.


 находим из:
находим из:
 системы (6)
системы (6) находим, подставляя
находим, подставляя 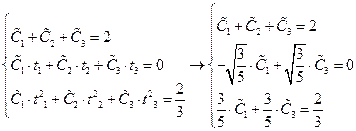
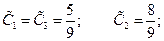

 находим из
находим из 
 находим с учетом соотношения:
находим с учетом соотношения:

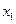 получаем:
получаем: 



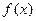 имеет непрерывность производной до шестого прядка, то для оценки погрешности формулы Гаусса с тремя узлами можно использовать неравенство:
имеет непрерывность производной до шестого прядка, то для оценки погрешности формулы Гаусса с тремя узлами можно использовать неравенство:

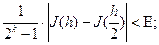
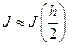 с точностью Е
с точностью Е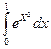 по квадратной формуле Гаусса с тремя узлами для n=1, т.е. без разбиения отрезка
по квадратной формуле Гаусса с тремя узлами для n=1, т.е. без разбиения отрезка 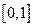 на части (n=1)
на части (n=1)
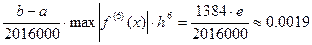

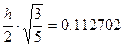 f(x1) = 1.012783
f(x1) = 1.012783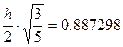 f(x1) = 2.19745
f(x1) = 2.19745


