Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы изолированные и неизолированные.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изолированная система (замкнутая cистема) — термодинамическая система, которая не обменивается с окружающей средой ни веществом, ни энергией. В термодинамике постулируется (как результат обобщения опыта), что изолированная система постепенно приходит в состояние термодинамического равновесия, из которого самопроизвольно выйти не может (нулевое начало термодинамики).
Диссипация энергии в диссипативной системе Диссипация энергии (лат. dissipatio) — рассеяние. Переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте — в теплоту. Системы, в которых энергия упорядоченного движения с течением времени убывает за счёт диссипации, переходя в другие виды энергии, например в теплоту или излучение, называются диссипативными. Для учёта процессов диссипации энергии в таких системах при определённых условиях может быть введена диссипативная функция. Если диссипация энергии происходит в замкнутой системе, то энтропия системы возрастает. Диссипация энергии в открытых системах, обусловленная процессами уноса энергии из системы, например в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энергии системы и окружающей среды. Это, в частности, обеспечивает важную роль процессов диссипации энергии в уменьшении удельной энтропии вещества на стадиях образования галактик и звёзд в модели горячей Вселенной. Диссипативная система (или диссипативная структура, от лат. dissipatio — «рассеиваю, разрушаю») — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации(рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой. Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве, то есть невыполнение Теоремы Лиувилля. Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова — Жаботинского и биологическая жизнь.
Термин «диссипативная структура» введен Ильёй Пригожиным. Последние исследования в области «диссипативных структур» позволяют делать вывод о том, что процесс «самоорганизации» происходит гораздо быстрее при наличии в системе внешних и внутренних «шумов». Таким образом, шумовые эффекты приводят к ускорению процесса «самоорганизации».
Работа переменной силы.
Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.
Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле
Разобьем отрезок [а; b] на п отрезков одинаковой длины
и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:
Поскольку An при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 1010; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.01 с.) |

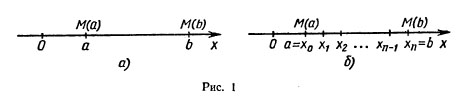
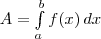 (1)
(1)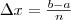 .Это отрезки [а; x1], [x1; x2],..., [xn-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x1] работа силы на этом отрезке приблизительно равна f (а) (x1—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x1; x2] приближенно равна f (x1) (x2 — x1) и т. д.; работа силы на n-ом отрезке приближенно равна f (xn-1)(b — xn-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна:
.Это отрезки [а; x1], [x1; x2],..., [xn-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x1] работа силы на этом отрезке приблизительно равна f (а) (x1—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x1; x2] приближенно равна f (x1) (x2 — x1) и т. д.; работа силы на n-ом отрезке приближенно равна f (xn-1)(b — xn-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна: