
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение взаимно перпендикулярных колебаний. Фигура лиссажу.
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
и заменяя во втором уравнении
Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2,...). В этом случае эллипс становится отрезком прямой
где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой, которое совершается вдоль прямой (3), составляющей с осью х угол. В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид
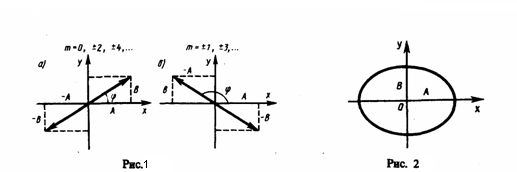
Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
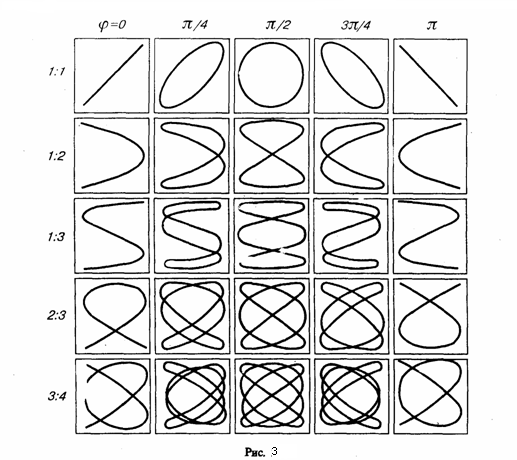
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ).
Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
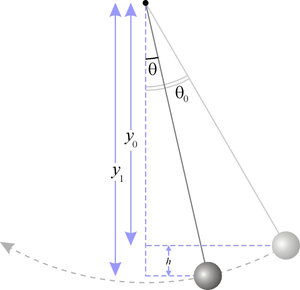
Математический маятник Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебанийматематического маятника длины l неподвижно подвешенного в однородном поле тяжести сускорением свободного падения g равен
и не зависит[1] от амплитуды и массы маятника. Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы. При малых колебаниях физический маятник колеблется так же, как математический сприведённой длиной. Физический маятник(приведенная длина, точка качения и их св-ва, вывод формулы периода). Физический маятник —осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Физический маятник Период колебаний физического маятника выражается по следующей формуле:
Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника. [править]Вычисление Приведённая длина вычисляется следующим образом:
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился. Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен Вывод формулы: Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на
Интегрируя это уравнение, получаем.
где
Отделяем переменные и интегрируем это уравнение:
Удобно сделать замену переменной, полагая
Здесь
Здесь -Период малых колебаний физического маятника Если амплитуда колебаний
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.108.168 (0.011 с.) |
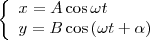 (1)
(1)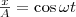
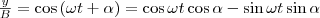
 на
на 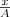 и
и 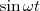 на
на 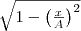 , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: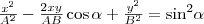 (2)
(2)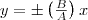 (3)
(3)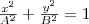 (4)
(4)

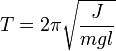
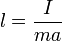
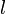 от точки подвеса. Эта точка и будет центром качания маятника.
от точки подвеса. Эта точка и будет центром качания маятника.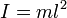 , а момент силы тяжести относительно той же оси
, а момент силы тяжести относительно той же оси 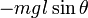 . Легко заметить, что уравнение движения не изменится.
. Легко заметить, что уравнение движения не изменится.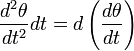 , а правую часть на
, а правую часть на 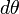 . Тогда:
. Тогда: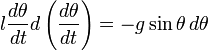 .
.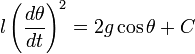 ,
,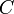 произвольная постоянная. Её можно найти из граничного условия, что в моменты
произвольная постоянная. Её можно найти из граничного условия, что в моменты 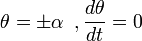 . Получаем:
. Получаем: 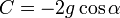 . Подставляем и преобразовываем получившееся уравнение:
. Подставляем и преобразовываем получившееся уравнение: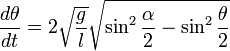 .
.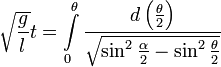 .
.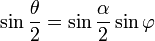 . Тогда искомое уравнение принимает вид:
. Тогда искомое уравнение принимает вид: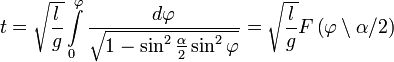 .
.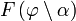 — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
— нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу: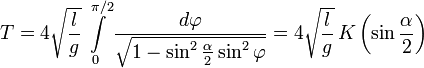 .
.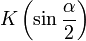 — полный нормальный эллиптический интеграл Лежандра 1-го рода.
— полный нормальный эллиптический интеграл Лежандра 1-го рода.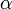 мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:
мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний: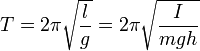 .
.


