
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение обыкновенных дифференциальных уравнений. Построение интегральной кривой. Метод Эйлера.
Решение обыкновенных дифференциальных уравнений. Задача Коши. Определение. Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функций:
Наивысший порядок n входящей в уравнение производной называется порядком дифференциального уравнения. Решением дифференциального уравнения называется всякая n раз дифференцируемая функция Для решения обыкновенных дифференциальных уравнений применяется метод конечных разностей. Его сущность состоит в следующем: 1. Область непрерывного изменения аргумента (например, отрезок) заменяется дискретным множеством точек – узлами. Эти узлы составляют разностную сетку. 2. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке (сеточной функцией). 3. Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена дифференциального уравнения разностным называется его аппроксимацией на сетке (или разностной аппроксимацией). Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки. Рассмотрим задачу Коши:
для определенности будем считать, что решение нужно получить для значений Метод Эйлера. Простейшим численным методом решения задачи Коши для обыкновенных дифференциальных уравнений является метод Эйлера. Он в основном используется как учебный, в практических расчетах он дает значительную погрешность. Рассмотрим дифференциальное уравнение первого порядка Но проблема в том, что переменные в уравнении Идея метода Эйлера состоит в том, чтобы заменить фрагмент графика
Заменим в левой части уравнения
Будем считать для простоты узлы равноотстоящими, т.е. С помощью метода Эйлера значение сеточной функции yi+1 в любом узле x i+1 вычисляется по ее значению yi в предыдущем узле x i. В связи с этим метод Эйлера относится к одношаговым методам. Графической иллюстрацией приближённого решения является ломаная, соединяющая последовательно точки P (xi; yi), которую называют ломаной Эйлера.
Для оценки погрешности на практике пользуются двойным просчетом: с шагом h и шагом h/2. Погрешность более точного значения
где yi – приближенное значение, полученное при вычислениях с шагом h, Пример. Найти частное решение дифференциального уравнения Точное решение данного уравнения имеет вид:
Необходимо найти и построить ломаную, которая приближает график функции M 1(0,1; y 1), M 2(0,2; y 2), M 3(0,3; y 3),…, M 9(0,9; y 9), M 10(1; y 10) Осталось найти y 1, y 2, y 3, …, y 9, y 10. Каждое следующее значение получается из предыдущего по простой рекуррентной формуле:
Представим дифференциальное уравнение
Таким образом: Начинаем с начального условия
Результаты вычислений удобно заносить в таблицу:
Чтобы улучшить приближение, необходимо измельчить разбиение. Разделим отрезок [0; 1], например, на 20 частей. Тогда шаг составит:
Вопросы для самопроверки 1. В чем заключается задача аппроксимации функции? 2. Какой многочлен называется интерполяционным? 3. Что такое численное дифференцирование? Когда оно применяется? 4. Какие формулы численного дифференцирования вам известны? 5. Что такое численное интегрирование? В каких случаях оно применяется? 6. Какие методы численного интегрирования вам известны? Охарактеризуйте каждый из них? 7. Что называют обыкновенным дифференциальным уравнением? 8. Сформулируйте задачу Коши для дифференциального уравнения первого порядка. 9. С помощью какого метода можно решить задачу Коши для обыкновенного дифференциального уравнения первого порядка? 10. В чем состоит суть метода Эйлера? Задания для самостоятельного решения Задание № 1. 1.Вычислить приближенное значение производной функции с использованием формулы, основанной на первой интерполяционной формуле Ньютона. Найти абсолютную и относительную погрешность результата.
2.Вычислить приближенное значение производной функции с использованием формулы, основанной на первой интерполяционной формуле Ньютона. Найти абсолютную и относительную погрешность результата.
Задание № 2. 1. Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,0001. Разбиение начать с двух отрезков 2 n = 2
2. Вычислить приближенное значение определенного интеграла 3. Вычислить приближенное значение определенного интеграла 4. Вычислить 5. Вычислить методом прямоугольников 6. Вычислить методом трапеций 7. Вычислить методом трапеций 8. Вычислить
9. Вычислить 10. Вычислить Задание № 3. Применяя метод Эйлера, численно решить данные дифференциальные уравнения с данными начальными условиями на отрезке [ a; b ] и с шагом h = 0,1 при указанных значениях параметров. 1. 2. 3. 4. 5.
VIII. Основы теории вероятностей и математической статистики Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира. В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая. Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить. Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении. Математическая статистика- это раздел математики, который имеет своим предметом изучения методов сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия решений. При этом под статистическими данными понимается совокупность чисел, которые представляют количественные характеристики интересующих нас признаков изучаемых объектов. Статистические данные получаются в результате специально поставленных опытов, наблюдений. Статистические данные по своей сущности зависят от многих случайных факторов, поэтому математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой. Основные понятия комбинаторики 1) В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,…, 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п. Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).
Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Предварительно познакомимся с понятием факториала. Произведение всех натуральных чисел от 1 до n включительно называют n- факториалом и пишут
Запомним, что 0!=1 и 1!=1. Используя знак факториала, можно, например, записать
Пример. Вычислить: а) а) Так как Тогда получим
б) Перестановки. Определение. Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Р n, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation - перестановка). Число перестановок можно вычислить по формуле
или с помощью факториала:
Пример. Сколькими способами можно расставлять на одной полке шесть различных книг? Искомое число способов равно числу перестановок из 6 элементов, т.е.
Пример. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что все числа не повторяются. Так как число кратно пяти, следовательно, цифра пять должна стоять на последнем месте. Остальные пять цифр могут стоять на оставшихся местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е.
3) Размещения. Определение. Пусть имеется множество, содержащее n элементов. Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования. Размещения обозначаются символом При этом полагают, что m Число размещений можно вычислить по формуле
т.е. число всех возможных размещений из n элементов по m равно произведению m последовательных целых чисел, из которых большее есть n. Запишем эту формулу в факториальной форме:
Пример. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов? Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.
Пример. В группе 20 учащихся. Сколькими способами могут быть выбраны староста и заместитель старосты? Искомое число вариантов равно числу размещений из 20 элементов по 2 элемента, т.е.
Пример. Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных урока? Число способов равно числу размещений из 7 элементов по 4, т.е. равно
Сочетания. Определение. Сочетаниямииз n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. (Подмножества, отличающиеся друг от друга только порядком следования элементов, не считаются различными.) Число сочетаний из n элементов по m обозначается символом В общем случае число из n элементов по m равно числу размещений из n элементов по m, деленному на число перестановок из n элементов:
Используя для чисел размещений и перестановок факториальные формулы, получим:
Пример. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать? Так как порядок выбранных четырех человек не имеет значения, то это можно сделать Находим по первой формуле
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
(по определению полагают
Пример. Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз? Матчей состоится столько, сколько существует двухэлементных подмножеств у множества, состоящего из 16 элементов, т.е. их число равно т.е. всего будет сыграно 120 матчей. Решение комбинаторных задач Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать? Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.
Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать? Решение.
Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно? Решение.
Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера? Решение. Солдат в дозор можно выбрать
способами, а офицеров Задача 5. Найти Решение. Так как
По определению сочетания следует, что
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.156.75 (0.324 с.) |
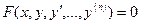
 , которая после ее подстановки в уравнение превращает его в тождество.
, которая после ее подстановки в уравнение превращает его в тождество.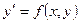 ,
,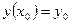
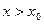 .
. правой разностью. При этом значения функции y в узлах x i заменим значениями сеточной функции yi:
правой разностью. При этом значения функции y в узлах x i заменим значениями сеточной функции yi: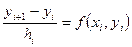
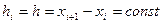 . Тогда из равенства
. Тогда из равенства 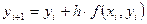

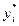 (при шаге h/2) оценивают приближенно так:
(при шаге h/2) оценивают приближенно так: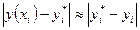
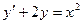 , соответствующее начальному условию
, соответствующее начальному условию 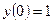 , методом Эйлера на отрезке [0; 1] с шагом h = 0,1. Построить таблицу и график приближённого решения.
, методом Эйлера на отрезке [0; 1] с шагом h = 0,1. Построить таблицу и график приближённого решения.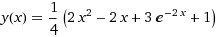
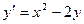

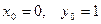
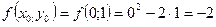
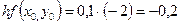
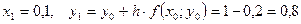
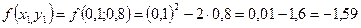
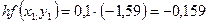

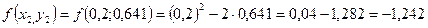

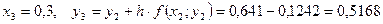
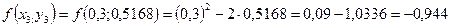
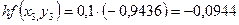
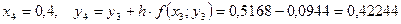
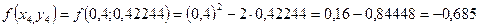
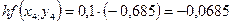

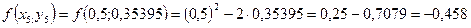
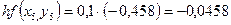
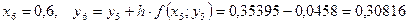
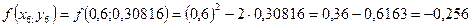
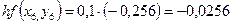

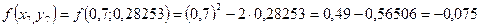
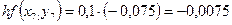
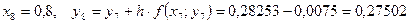

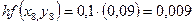

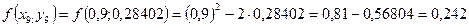

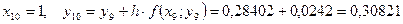
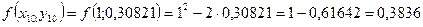
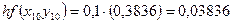
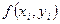


 Существенным недостатком простого метода Эйлера является слишком большая погрешность, при этом легко заметить, что погрешность имеет тенденцию накапливаться – чем дальше мы уходим от точки M 0, тем преимущественно больше становится расхождение между приближением и истиной. Это объяснимо самим принципом, который Эйлер положил в основу своего метода: отрезки M 0 M 1, M 1 M 2, M 2 M 3,…, M 9 M 10 параллельны соответствующим касательным к графику функции
Существенным недостатком простого метода Эйлера является слишком большая погрешность, при этом легко заметить, что погрешность имеет тенденцию накапливаться – чем дальше мы уходим от точки M 0, тем преимущественно больше становится расхождение между приближением и истиной. Это объяснимо самим принципом, который Эйлер положил в основу своего метода: отрезки M 0 M 1, M 1 M 2, M 2 M 3,…, M 9 M 10 параллельны соответствующим касательным к графику функции 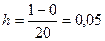 , и совершенно понятно, что ломаная из 20 звеньев заметно точнее приблизит частное решение. С помощью Excel не составит труда обработать 100-1000 и даже миллион промежуточных отрезков
, и совершенно понятно, что ломаная из 20 звеньев заметно точнее приблизит частное решение. С помощью Excel не составит труда обработать 100-1000 и даже миллион промежуточных отрезков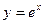 в точке x = 3,62 и x = 3,80
в точке x = 3,62 и x = 3,80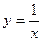 в точке x = 2,718 и x = 2,780
в точке x = 2,718 и x = 2,780
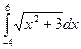 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой. с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой..
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой..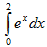 методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.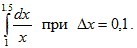
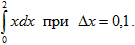
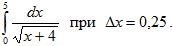
 разделив отрезок [0;4] на 40 равных частей.
разделив отрезок [0;4] на 40 равных частей. разделив отрезок [0;8] на 40 равных частей.
разделив отрезок [0;8] на 40 равных частей.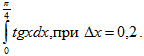
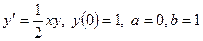

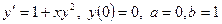


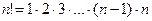 .
.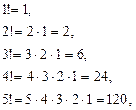
 ; б)
; б) 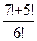 .
.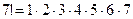 и
и 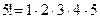 , то можно вынести за скобки
, то можно вынести за скобки 
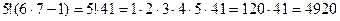 .
.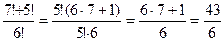 .
.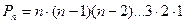

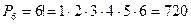 .
.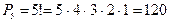 .
.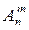 , где n - число всех имеющихся элементов, m - число элементов в каждой комбинации. (А- первая буква французского слова arrangement, что означает «размещение, приведение в порядок»).
, где n - число всех имеющихся элементов, m - число элементов в каждой комбинации. (А- первая буква французского слова arrangement, что означает «размещение, приведение в порядок»).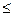 n.
n.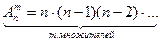 ,
,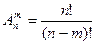 .
.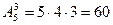 .
.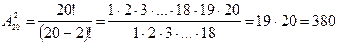
 По формуле получаем
По формуле получаем 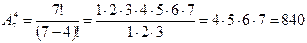
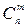 (С -первая буква французского слова combination - сочетание).
(С -первая буква французского слова combination - сочетание).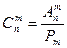
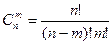
 способами.
способами.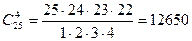 .
.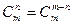

 и
и 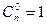 );
);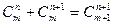 .
.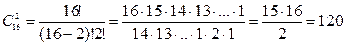 ,
, .
.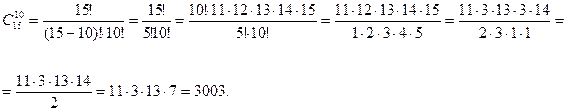
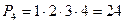 .
.
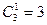 способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется
способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется 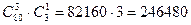 способов.
способов.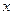 , если известно, что
, если известно, что  .
.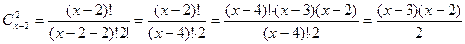 , то получим
, то получим ,
,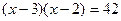 ,
, ,
,
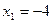 ,
, 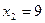 .
. ,
,  . Т.о.
. Т.о. 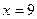 .
.


