
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отсюда, подставляя (3.4) в (3.2), (3.3), получим:
Для периода, равного одному году (t=1), из (3.5.) получим соотношения: Если единичная сумма инвестируется в начале года под проценты по ставке i, то в конце года проценты на эту сумму составят 1× i, а текущее значение этой величины будет определяться выражениями (3.6). Это означает, что дисконт можно рассматривать как проценты, но уплачиваемые не в конце года (периода), а в начале, поэтому иногда дисконтную ставку называют авансированной процентной ставкой. Формулы (3.2), (3.3) и (3.5) получены в предположении, что временные базы начисления процентной и учетной ставок одинаковы (напомним, что Если временные базы разные, например, при начислении процентов принята база 365 дней, а для учетной ставки – 360 дней, то ПРИМЕР 3.3 Найти текущую стоимость 100 долл., полученных через год: а) при процентной ставке 12,5 %; б) при учетной ставке 12,5 %. РЕШЕНИЕ. а) Для процентной ставки 12,5 % имеем:
и, следовательно,
б) Для учетной ставки 12,5 % имеем: S =100 долл., d =0,125 долл. t =1 год. Поэтому
ПРИМЕР 3.4 Простая годовая процентная ставка равна 15 %. Найти эквивалентные годовые учетные ставки для периодов: а) один месяц; б) полгода. РЕШЕНИЕ. а) В этом случае i =0,15, n = Если d – соответствующая годовая учетная ставка, то из уравнения эквивалентности (3.5 б)
б) Здесь i =0,15; n =
ПРИМЕР 3.5 Вексель учтен за год до даты его погашения по учетной ставке 15 %. Какова доходность учетной операции в виде процентной ставки? РЕШЕНИЕ По формуле (3.5. а)
Из последнего примера видно, что при одинаковых условиях операции d < i. Следует заметить, что отношения эквивалентности между простыми учетной и процентной ставками существенно зависят от срока операции: с увеличением срока разница между d и i тоже увеличивается.
Эквивалентность сложных ставок. Пусть ic, dc и j – сложные процентная, учетная и номинальная ставки, соответственно. Эквивалентность ставок ic и j устанавливается так же, как при получении формулы (2.13.) для эффективной ставки, т.е. из формулы 1+ i =(1+ j / m) m. Тогда Из формул для сложных процентов (2.8) и для дисконтирования по сложным процентам (2.18) следует связь между сложной процентной ставкой
Учитывая, что υ=(1+ic)-1, получим из последних формул: dc=iv, v=1-dc, ic-dc=idc. (3.13), (3.14), (3.15) ПРИМЕР 3.6 При разработке условий контракта стороны договорились о том, что доходность ссуды должна составлять 24 % годовых. Каков должен быть размер номинальной ставки при начислении процентов поквартально и ежемесячно? РЕШЕНИЕ. По формуле (3.10.) получим
т. е. номинальные ставки равны 22,1 и 21,7 % соответственно. Эквивалентность простых и сложных ставок Определим соотношение эквивалентности между простой и сложной ставками наращения. Для этого приравняем друг к другу соответствующие множители наращения при равенстве начальных P и наращенных S сумм:
где in и ic – ставки простых и сложных процентов, n – срок инвестирования. Тогда Заменив в формулах (3.16.) и (3.17.) i с на j / m, а n = m × t, где t – число лет, m – число раз начисления процентов в году, получим: Для эквивалентности сложной ставки i с процентов и учетной простой ставки dn имеем равенства:
Эквивалентность dn и номинальной сложной ставки j определяется:
ПРИМЕР 3.7 Заменить простую ставку 18 % на сложную годовую ставку, не изменяя финансовых последствий контракта сроком 2 года. РЕШЕНИЕ. По формуле (3.17) находим эквивалентную сложную ставку:
Эквивалентность сложных дискретных и непрерывных ставок
Эквивалентность между дискретной сложной ставкой i и силой роста
Поскольку
Тогда Аналогично устанавливается эквивалентность между непрерывной ставкой
ПРИМЕР 3.8 Какая непрерывная ставка заменит полугодовое начисление процентов по номинальной ставке 20 %? РЕШЕНИЕ. По формуле (3.29)
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.243 (0.008 с.) |
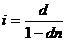 ; (3.5 а)
; (3.5 а)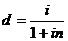 . (3.5 б)
. (3.5 б)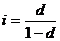 ; (3.6. а)
; (3.6. а)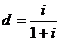 . (3.6.б)
. (3.6.б)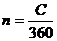 (или
(или 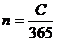 ), получим следующие соотношения эквивалентности:
), получим следующие соотношения эквивалентности: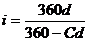 ;
; 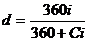 . (3.7)
. (3.7)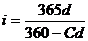 ;
; 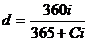 . (3.8)
. (3.8)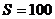 долл.; i =0,125; n =1 год
долл.; i =0,125; n =1 год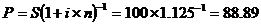 долл.
долл.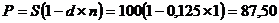 долл.
долл.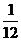 .
.
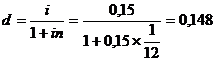 ; d = 14,8 %.
; d = 14,8 %.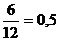 .
.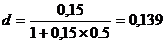 ; d =13,9 %.
; d =13,9 %.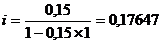 или 17,65 %.
или 17,65 %.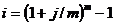 ;
; 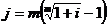 . (3.9), (3.10)
. (3.9), (3.10)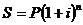 ;
; 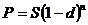 ;
;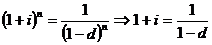 ;
;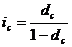 ;
; 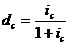 . (3.11.), (3.12)
. (3.11.), (3.12)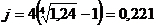 ;
; 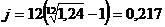 ,
,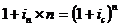 ,
,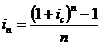 ;
; 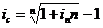 . (3.16), (3.17)
. (3.16), (3.17)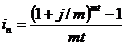 ;
; 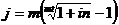 . (3.18), (3.19)
. (3.18), (3.19)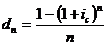 ;
; 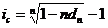 . (3.20), (3.21)
. (3.20), (3.21)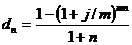 ;
; 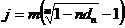 . (3.22), (3.23)
. (3.22), (3.23)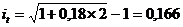 или 16,6 %.
или 16,6 %.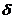 определена нами уравнениями (2.25) и (2.26):
определена нами уравнениями (2.25) и (2.26):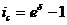 ;
; 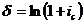 . (3.24), (3.25)
. (3.24), (3.25)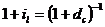 ;
; 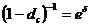 .
.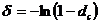 ;
; 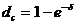 . (3.26), (3.27)
. (3.26), (3.27)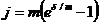 ;
; 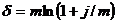 . (3.28), (3.29)
. (3.28), (3.29)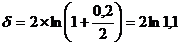 .
.


