
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула взаимосвязи производной по направлению и градиента ⇐ ПредыдущаяСтр 7 из 7
Доказательство. Обозначим координаты вектора
Это функция Рассмотрим производную композиции функций Производная внешней функции (которая действует последняя) это вектор-строка градиент функции f. Производная внутренней функции (которая действует первая) это вектор-столбец.
Но ведь
Но ведь это и есть скалярное произведение градиента и вектора
Отсюда виден геометрический смысл градиента: это вектор, при движении в направлении которого рост функции наиболее быстрый. Если движение в перпендикулярном направлении, то рост функции будет нулевым. Если под большим увеличением рассмотреть какой-то небольшой кусочек поверхности, то он выглядит почти как наклонная плоскость, а для наклонной плоскости при движении в ту сторону, куда она наклонена, наибольшая скорость роста высоты, в перпендикулярном направлении - высота не изменяется, а при движении в противоположном - уменьшается. Замечание. Если направление
Алгоритм вычисления производной по направлению можно условно разделить на 4 шага: 1) Найти градиент в произвольной точке, 2) Найти градиент в конкретной точке, 3) Нормировать вектор, задающий направление, 4) Скалярно умножить градиент в точке на этот нормированный вектор. Замечание. Шаги 3 и 4 перестановочны, то есть можно не нормировать вектор, а разделить на его длину получившееся скалярное произведение
Задача 266. Дана функция а) координаты вектора б) Решение. Найдём все 3 частных производных.
1) Градиент в произвольной точке: 2) Градиент в точке 3) Нормируем вектор Нормированный вектор 4) Скалярно умножим его на градиент в точке, т.е.
Ответ. Задача 267. Дана функция а) координаты вектора б) Решение. Ищем частные производные.
Итак, градиент
Ответ. Задача 268. Найти градиент функции Решение. Градиент в произвольной точке: Градиент в конкретной точке: Нормируем вектор (1,3). Скалярно умножим Ответ. Задача 269. Дана функция а) координаты вектора б) Решение. Частные производные:
Присвоим конкретные значения Учитывая, что
Нормируем вектор Итак, надо рассматривать такой вектор: Теперь скалярно умножим его на градиент.
Ответ. Задача 270. Найти градиент функции Решение. 1) Вычисляем частные производные: 2) 3) Скалярно умножаем 4) Разделим на Ответ. Задача 271. Найти градиент функции Решение. 1. 2. 3. Нормируем вектор a = (1,0,1). Его модуль 4. Скалярно умножим Получим Ответ. * Задача домашняя. Найти градиент функции Ответ. Градиент
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.24 (0.016 с.) |
 .
.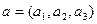 . Точка M произвольная, её координаты
. Точка M произвольная, её координаты  , а точка
, а точка  . Так как
. Так как 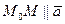 то их координаты пропорциональны, то есть
то их координаты пропорциональны, то есть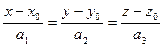 , что также записывается в параметрическом виде:
, что также записывается в параметрическом виде: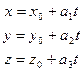
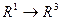 .
.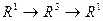 , а именно
, а именно 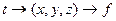 . Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.
. Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.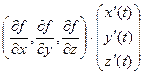
 , аналогично
, аналогично 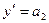 и
и  . Тогда
. Тогда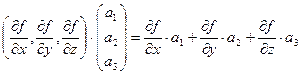
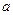 .
.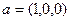 , скалярное произведение этого вектора и градиента
, скалярное произведение этого вектора и градиента  это
это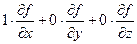 =
= 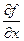 .
.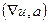 .
. . Найти:
. Найти: 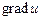 в точке
в точке  ,
,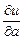 в точке
в точке 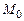 в направлении вектора
в направлении вектора 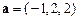 .
.  =
= 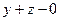 .
.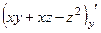 =
=  .
.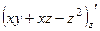 =
= 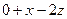 .
. .
. 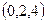 .
. 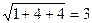 .
.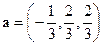 .
.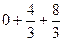 =
= 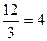 .
. 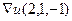 =
=  . Найти:
. Найти: 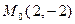 ;
;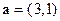 .
. 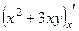 =
= 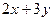 ,
, 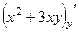 =
= 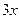 .
. . При
. При 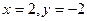 получаем вектор
получаем вектор 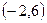 . Нормируем вектор
. Нормируем вектор 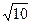 . Новый вектор
. Новый вектор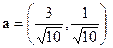 . Скалярно умножаем его на
. Скалярно умножаем его на  .
.  ,
,  в точке (1,1) и производную по направлению (1,3).
в точке (1,1) и производную по направлению (1,3).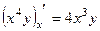 ,
,  .
.
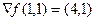
 .
. и
и 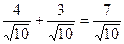 .
.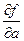 =
= 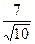 .
. . Найти:
. Найти: 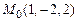
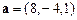 .
. 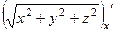 =
=  =
= 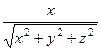 . Аналогично
. Аналогично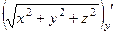 =
= 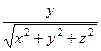 ,
, 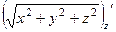 =
= 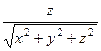 .
. и получим градиент в точке.
и получим градиент в точке.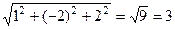 ,получится:
,получится:  .
. .
.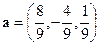 .
.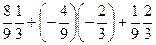 =
= 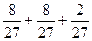 =
= 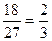 .
.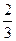 .
.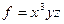 в точке
в точке 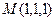 и производную по направлению
и производную по направлению 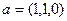 .
. .
. 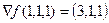 .
.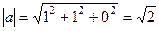 , получим
, получим 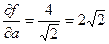 .
. ,
, 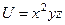 в точке (1,2,3) и производную по направлению a = (1,0,1).
в точке (1,2,3) и производную по направлению a = (1,0,1). 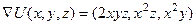 .
.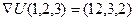
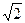 . Тогда нормированный вектор:
. Тогда нормированный вектор: 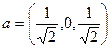 .
.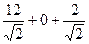 =
=  =
= 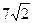 .
.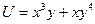 в точке (2,2) и производную по направлению a = (3,4).
в точке (2,2) и производную по направлению a = (3,4). ,
, 


