
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость графика и 2-я производная.
Задача 258. Найти интервалы выпуклости вверх и выпуклости вниз графика функции Решение. Сначала, очевидно, надо найти первую производную.
Первая производная положительна, она может обратиться в 0 лишь при Теперь найдём 2-ю производную.
Сократим по крайней мере на одну степень выражения
= 1) 2) Теперь сопоставим эти интервалы, вот на схеме жёлтым показано, на каком интервале то или иное выражение положительно, а зелёным - отрицательно:
Итак, На этих интервалах график выпуклый вниз.
На этих интервалах график выпуклый вверх. Ответ.
Точки перегиба
Задача 259. Найти интервалы выпуклости вверх (вниз) графика функции Решение.
Впрочем, строение такой гиперболы хорошо известно: на правой полуоси график пройдёт ниже хорды, а на левой выше. Чертёж:
Ответ. Выпуклый вниз при
Задача 260. Найти интервалы выпуклости вверх (вниз) графика функции Решение.
Ответ. Выпуклый вниз в Проект далее.
«Частные производные, градиент». Рассмотрим производные для функций нескольких переменных
Можно задать приращение только для Определение. Производной функции f по переменной x называется предел: Кроме Аналогично определяется частная производная по y, ведь можно взять вторую точку, отступив в направлении другой оси.
Геометрический смысл: тангенс угла наклона касательной к кривой, получающейся в одном из сечений. Физический смысл. Если функция - это температура воздуха, то например, при движении самолёта строго на юг температура за бортом будет возрастать, а при движении на запад или восток почти неизменна. Как видим, частные производные в двух перпендикулярных направлениях могут сильно отличаться.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.224 (0.007 с.) |
 .
.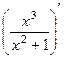 =
= 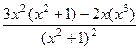 =
= 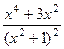 .
. 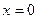 . Так как она нигде не отрицательна (ведь все степени чётные) то интервал роста не сменяется интервалом убывания, а снова продолжается рост. Таким образом, мы установили, что экстремумов нет, функция монотонно возрастает.
. Так как она нигде не отрицательна (ведь все степени чётные) то интервал роста не сменяется интервалом убывания, а снова продолжается рост. Таким образом, мы установили, что экстремумов нет, функция монотонно возрастает. 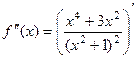 =
= 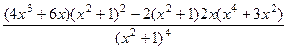
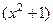 .
.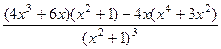 =
= 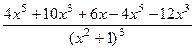 =
=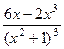 =
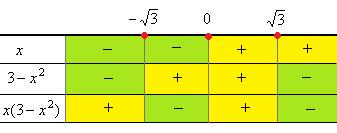
= 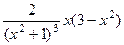 выделили множитель, который заведомо больше 0, а также там видим 2 множителя, которые могут менять знак. Когда они одного знака, оба плюс или минус, тогда вторая производная больше 0, а когда разного знака, тогда меньше 0.
выделили множитель, который заведомо больше 0, а также там видим 2 множителя, которые могут менять знак. Когда они одного знака, оба плюс или минус, тогда вторая производная больше 0, а когда разного знака, тогда меньше 0.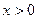 на
на 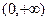 ,
,  на
на 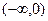 .
.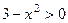
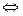
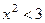
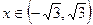 .
.
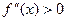 , если
, если 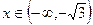 и
и 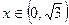 .
.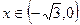 и
и 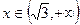 .
.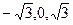 .
.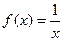 .
.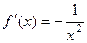 ,
, 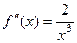 .
.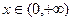 , график выпуклый вниз.
, график выпуклый вниз.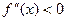 при
при 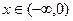 , график выпуклый вверх.
, график выпуклый вверх.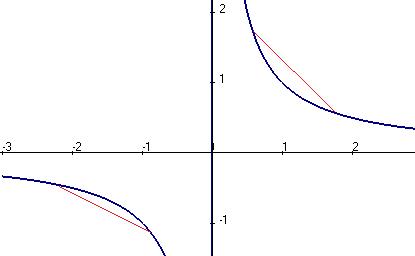
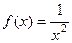 .
.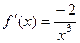 ,
, 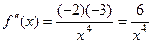 .
.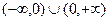 , график выпуклый вниз. График:
, график выпуклый вниз. График: 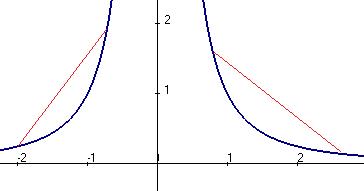
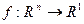 . Пусть например, дана функция
. Пусть например, дана функция 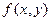 , или
, или 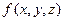 . Приращение аргумента в этом случае задаётся не однозначным образом: ведь можно задать приращение каждому из аргументов, которых несколько. Так, например, для
. Приращение аргумента в этом случае задаётся не однозначным образом: ведь можно задать приращение каждому из аргументов, которых несколько. Так, например, для 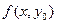 . Это уже будет функция одной переменной. График функции
. Это уже будет функция одной переменной. График функции 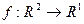 это поверхность, тогда при фиксировании
это поверхность, тогда при фиксировании 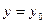 получается сечение поверхности вертикальной плоскостью, то есть кривая.
получается сечение поверхности вертикальной плоскостью, то есть кривая.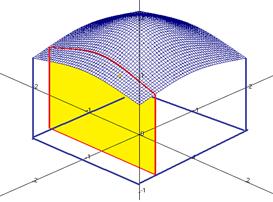
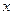 , и тогда получим такое понятие, как частная производная.
, и тогда получим такое понятие, как частная производная. 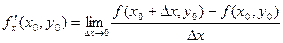 .
.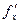 ещё применяют такое обозначение:
ещё применяют такое обозначение: 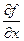 .
.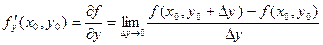 .
.


