Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод вычисления частных производных.
Если бы вам нужно было вычислить производную функции, содержащей параметр C, например Пример 261.
Пример 262.
Если объединить частные производные в один вектор, то получим этот вектор называется градиентом функции. Кроме Если после вычисления частных производных фиксировать переменные, то есть взять конкретную точку, то получится градиент в точке. Это вектор, состоящий из чисел, а не функций. Пример. Пусть
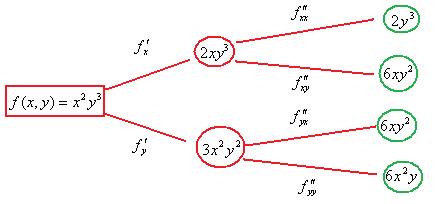
И действительно, если точка находится под этой поверхностью, то она должна двигаться в направлении от центра, чтобы рост высоты поверхности над ней происходил быстрее всего. Производные высшего порядка. После дифференцрования по той или иной переменной, мы получаем снова функцию от тех же нескольких переменных. Её снова можно продифференцровать по одной или другой переменной. Таким образом, получается n2 возможностей определить какие-либо вторые производные, например, если две переменных, то вторых производных будет четыре:
Покажем их нахождение в виде схемы:
Смешанные вторые производные Также применяются и такие обозначения:
Задача 263. Дана функция Решение. Найдём две частных производных.
Градиент в произвольной точке: Кстати, для получившегося векторного поля функция Градиент в точке Ответ. Задача 264. Дана функция Решение.
Градиент в произвольной точке: Градиент в точке Ответ. Практика 25. Задача 265. Найти градиент функции
Решение. Найдём частные производные. Ответ. Производная по направлению. В определении частных производных, мы рассматривали приращение аргумента в виде
называется «производная по направлению». Будем считать, что вектор нормирован, то есть
Если это направление соответствует какой-либо из координатных осей, то как раз и получаются частные производные, которые изучили раньше.
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.255.189 (0.006 с.) |
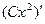 , то понятно, что
, то понятно, что  . Так вот, аналогично, если функция нескольких переменных, то при дифференцировании по одной из них, остальные в роли параметров, то есть вы можете мысленно «заморозить» их или даже переобозначить через A или C, а после вычисления производной, разморозить или переобозначить обратно.
. Так вот, аналогично, если функция нескольких переменных, то при дифференцировании по одной из них, остальные в роли параметров, то есть вы можете мысленно «заморозить» их или даже переобозначить через A или C, а после вычисления производной, разморозить или переобозначить обратно. тогда:
тогда: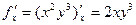 ,
, .
. тогда:
тогда: ,
, ,
,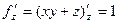 .
.  .
. , применяется обозначение
, применяется обозначение 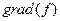 .
.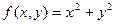 . Соответствующая поверхность - эллиптический параболоид. Градиент поверхности это вектор
. Соответствующая поверхность - эллиптический параболоид. Градиент поверхности это вектор 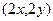 . Теперь, если фиксировать точку (1,0) то получим, что градиент равен (2,0) а если точку (1,1) то (2,2) и т.д. Градиент для этой функции всегда направлен радиально от начала координат.
. Теперь, если фиксировать точку (1,0) то получим, что градиент равен (2,0) а если точку (1,1) то (2,2) и т.д. Градиент для этой функции всегда направлен радиально от начала координат.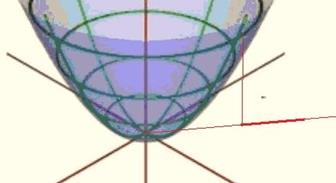
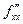 ,
,  ,
, 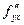 ,
,  .
.
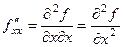 ,
,  ,
,  ,
, 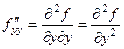 .
. . Найти координаты вектора
. Найти координаты вектора  в точке
в точке  .
. =
= 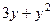 ,
, 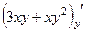 =
=  .
. .
.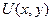 называется потенциалом.
называется потенциалом.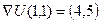 .
.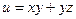 . Найти
. Найти 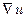 в точке
в точке  .
.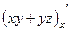 =
=  ,
, 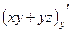 =
= 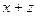 ,
,  =
=  .
. .
.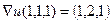 .
. в точке (1,1,1).
в точке (1,1,1).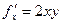 ,
, 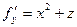 ,
, 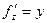 . Присвоим все значения x,y,z=1. Получаем
. Присвоим все значения x,y,z=1. Получаем  .
.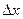 или
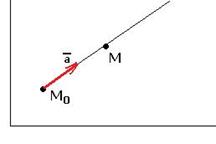
или 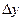 . Но ведь от исходной точки можно отступить не только в направлении координатных осей, но и в произвольном направлении. Если рассмотреть разность значений функции в какой-то паре точек, расположенных произвольно, а не вдоль оси, то есть
. Но ведь от исходной точки можно отступить не только в направлении координатных осей, но и в произвольном направлении. Если рассмотреть разность значений функции в какой-то паре точек, расположенных произвольно, а не вдоль оси, то есть 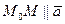 и затем приближать 2-ю точку к первой, и при этом делить
и затем приближать 2-ю точку к первой, и при этом делить  на расстояние между точками, получим предел
на расстояние между точками, получим предел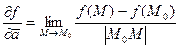
 . Только в этом случае мы получим правильный результат, ведь нужно измерять скорость изменения функции именно в расчёте на единицу длины при движении по этой прямой.
. Только в этом случае мы получим правильный результат, ведь нужно измерять скорость изменения функции именно в расчёте на единицу длины при движении по этой прямой.