
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 238. Вывод уравнения касательной.
Рассмотрим треугольник, его катеты равны
Возьмём теперь точку Запишем пропорцию координат так, как это всегда делали в теме «аналитическая геометрия». Получается каноническое уравнения прямой: Замечание. Уравнение касательной можно запомнить в виде
Задача 239-А. Найти касательную к графику Решение. Ответ. Задача 239-Б. Найти дифференциал функции Решение. Дифференциал: Приближённые вычисления (1,1)^2 = 1,21 с пом dx 1,2
Задача 240. Найти касательную к графику Решение.
Ответ. Уравнение касательной Задача 241. Найти касательную к графику Решение.
Подставим эту информацию в уравнение Получается Надо применить формулу расстояния от точки до прямой в плоскости:
для этого сначала преобразуем к неявному виду: Тогда видно, что
Ответ. Касательная Задача 242. На графике функции Решение. Производная в некоторой точке равна 4. Если Общий вид уравнения касательной: Тогда в данном случае: Ответ. Точка Задача 243. Найти точки на графике Решение. Построим уравнение касательной при произвольной абсциссе. Пусть абсцисса
Задача дом. Аналогично прошлой задаче, для точки (1,1). – дом. задание. Ответ. Задача дом. Найти уравнение касательной к кривой Задача дом. Найти уравнение касательной к кривой Задача дом. Найти уравнение касательной для
Практика 23. Задача 244. Найти касательные к графику Решение. Во-первых, Ищем касательную в 1-й точке.
Ищем касательную во 2-й точке.
Решаем систему уравнений, ищем пересечение этих прямых:
Вычтем из 2-го 1-е. Тогда Ответ.
Задача 245. Найти предел Решение. Метод разложения на множители, при степени 3 и выше, более трудоёмкий Сначала поделить каждый многочлен на По методу Лопиталя: применять можно, условия теоремы выполнены, так как конечное число корней и они изолированы, то есть существует окрестность, в которой нет других корней знаменателя.
Снова получается неопределённость
Ответ. Задача 246. Найти предел Решение. Методом Лопиталя =
Продифференцируем ещё раз
Монотонность и экстремумы. Опр. 1 (точки наибольшего, наименьшего значения в D). Пусть функция f - функция одной переменной, т.е. отображает некоторое множество Опр. 2. (максимум и минимум) Пусть функция Для максимума и минимума есть общее название - «экстремум».
Локальных максимумов может быть несколько, или даже бесконечное количество. Например, график
Понятие «максимум» отличается от понятия «наибольшее значение» тем, что для максимума требуется, чтобы функция была наибольшей в некоторой окрестности, а для наибольшего значения - во всей области.
Теорема Ферма (необходимый признак экстремума). Если функция дифференцируема в точке Прим. 1) 2) для
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.253 (0.022 с.) |
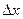 и
и 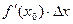 , так как тангенс угла наклона касательной это
, так как тангенс угла наклона касательной это 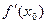 . Направляющий вектор для прямой направлен в точности по гипотенузе. При этом, мы можем пропорционально увеличить этот треугольник, тогда катеты будут такие: 1 и
. Направляющий вектор для прямой направлен в точности по гипотенузе. При этом, мы можем пропорционально увеличить этот треугольник, тогда катеты будут такие: 1 и  .
.
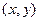 где-нибудь на касательной. Она принадлежит касательной в точности тогда, когда вектор
где-нибудь на касательной. Она принадлежит касательной в точности тогда, когда вектор 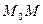 коллинеарен направляющему вектору этой прямой, т.е.
коллинеарен направляющему вектору этой прямой, т.е.  .
. . А теперь просто умножим на
. А теперь просто умножим на 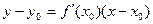 .
. причём, так запомнить легче.
причём, так запомнить легче.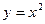 в точке
в точке 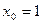 .
. ,
,  ,
, 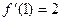 . Уравнение
. Уравнение 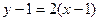 , то есть
, то есть  .
. .
. 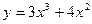 в точке
в точке  .
. 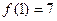 ,
,  ,
, 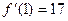 .
.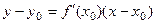
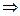
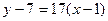
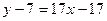
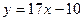 .
.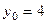 ,
, 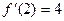 .
.
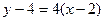
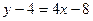
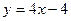 .
.
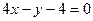 .
.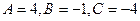 .
.  .
.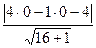 =
=  .
. взята точка
взята точка 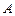 . Касательная к графику в точке
. Касательная к графику в точке 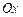 под углом, тангенс которого равен 4. Найти точку
под углом, тангенс которого равен 4. Найти точку  и уравнение касательной в этой точке.
и уравнение касательной в этой точке.  , то
, то 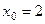 , тогда
, тогда  .
. .
. , касательная
, касательная  , такие, что касательные, проведённые в них, проходят через начало координат.
, такие, что касательные, проведённые в них, проходят через начало координат. . Тогда
. Тогда 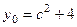 ,
, 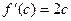 . Уравнение касательной
. Уравнение касательной  . Преобразуем его.
. Преобразуем его. 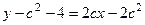
 . Чтобы не было константы, должно быть
. Чтобы не было константы, должно быть 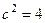 , т.е.
, т.е.  или
или  . Высота графика при обоих этих значениях одинакова, и равна 8. Тогда точки:
. Высота графика при обоих этих значениях одинакова, и равна 8. Тогда точки: 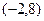 и
и 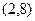 . Ответ.
. Ответ. 
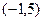 и
и  .
.  в точке
в точке  . Ответ.
. Ответ.  .
.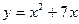 в точке
в точке 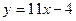 .
. в точке
в точке 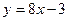 .
. в точках с абсциссами 1 и 2, и точку пересечения этих касательных.
в точках с абсциссами 1 и 2, и точку пересечения этих касательных.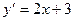 .
.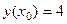 ,
, 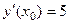 . Тогда
. Тогда 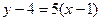 , что приводит к
, что приводит к
 .
.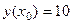 ,
, 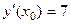 . Тогда
. Тогда  , что приводит к
, что приводит к 
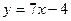 .
.
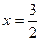
 .
.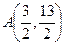 .
. 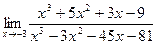 .
.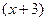 , останутся многочлены 2-й степени, корни которых можно найти через дискриминант. Будет множитель вида
, останутся многочлены 2-й степени, корни которых можно найти через дискриминант. Будет множитель вида  .
.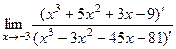 =
=  .
.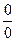 , поэтому 2-й шаг, здесь придётся дифференцировать 2 раза, из-за наличия корня кратности 2 у исходных многочленов.
, поэтому 2-й шаг, здесь придётся дифференцировать 2 раза, из-за наличия корня кратности 2 у исходных многочленов. 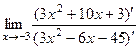 =
=  =
= 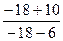 =
= 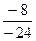 =
= 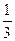 .
.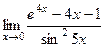 .
. =
= 
 . Но опять получилась неопределённость
. Но опять получилась неопределённость 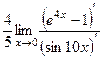 =
=  =
=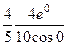 =
= 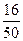 =
= 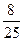 = 0,32. Ответ.
= 0,32. Ответ.  в
в 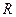 . Точка
. Точка 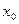 называется точкой наибольшего (соответственно, наименьшего) значения в D, если
называется точкой наибольшего (соответственно, наименьшего) значения в D, если 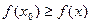
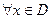 . (соответственно,
. (соответственно, 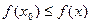
 . Точка
. Точка  точки
точки 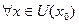 . (для минимума
. (для минимума 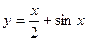 , здесь через каждые
, здесь через каждые 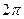 есть новый максимум:
есть новый максимум: 
 .
.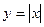 , минимум в точке 0, но там не существует производная, то есть нельзя сказать, что
, минимум в точке 0, но там не существует производная, то есть нельзя сказать, что 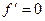 .
.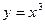 ,
, 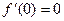 , но при этом нет экстремума.
, но при этом нет экстремума.


