
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные независимые испытания. испытания по схеме Бернулли
На практике приходится сталкиваться с такими задачами, которые можно представить виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появится событие Испытания называют повторно независимыми, если испытания являются независимыми и вероятность появления события Повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события Пусть производится В зависимости от значений · Если
где · Если
где Значения · Если
где Пример. Вероятность появления события 1) Событие 2) Событие Решение. По условию 1) Вероятность того что событие Искомая вероятность:
2) Событие
Искомая вероятность:
Пример. Процент всхожести семян Решение. Т.к. процент всхожести семян
Откуда По таблице значений функции
Искомая вероятность:
Пример. Вероятность того, что станок изготовит бракованное изделие постоянна и равна 1) ровно 2) не менее Решение. Вероятность изготовления бракованного изделия постоянна и равна
1) Среди изготовленных изделий ровно
Искомая вероятность:
2) Для определения вероятности того, что среди изготовленных деталей не менее
Событию, среди изготовленных деталей меньше Используя теорему сложения вероятностей несовместных событий и формулу Пуассона, найдем вероятность того, что среди изготовленных деталей меньше
Следовательно
Искомая вероятность:
Наивероятнейшим числом появления события Для определения наивероятнейшего числа не обязательно вычислять вероятности возможных чисел появлений события, достаточно знать число испытаний Для определения наивероятнейшего числа используют двойное неравенство:
Следует иметь в виду, что: 1) если 2) если
3) если Пример. Определить наивероятнейшее число качественных изделий в партии из Решение. По условию Используя неравенство:
имеем
откуда
Следовательно, наивероятнейшее число качественных изделий в партии из Предположим, что проводится
где
Пример. Вероятность того, что деталь изготовлена с нарушениями стандартов равна Решение. По условию Воспользуемся интегральной теоремой Лапласа:
найдем
По таблице значений функции
Искомая вероятность:
|
||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 55; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.05 с.) |
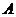 . При этом интерес представляет исход не каждого отдельного испытания, а общее количество появлений события
. При этом интерес представляет исход не каждого отдельного испытания, а общее количество появлений события 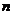 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 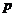 . Требуется найти вероятность
. Требуется найти вероятность 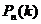 того, что при
того, что при 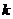 раз.
раз.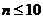 , то используют формулу Бернулли:
, то используют формулу Бернулли: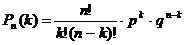 ,
, -вероятность не наступления события
-вероятность не наступления события 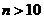 и
и 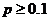 , то используют локальную теорему Лапласа:
, то используют локальную теорему Лапласа: ,
,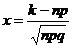 ,
, 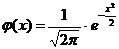 .
.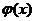 находят по таблице приложения 1. Функция
находят по таблице приложения 1. Функция 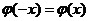 , таблица содержит значения функции
, таблица содержит значения функции 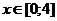 ; для
; для 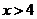 можно принять
можно принять  .
.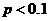 , (либо
, (либо 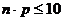 ) то используют формулу Пуассона:
) то используют формулу Пуассона: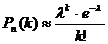 ,
,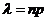 .
. независимых испытаний постоянна и равна
независимых испытаний постоянна и равна 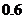 . Определить вероятность того, что:
. Определить вероятность того, что: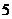 раз;
раз;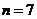 ;
; 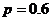 . Т.о. для решения задачи используют формулу Бернулли.
. Т.о. для решения задачи используют формулу Бернулли.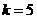 ;
; 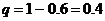 .
.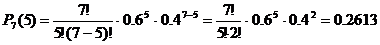 .
.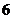 раз, или
раз, или 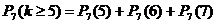 .
.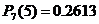 ;
;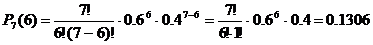 ;
;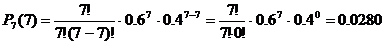 .
.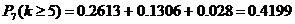 .
.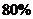 . Определить вероятность того, что из
. Определить вероятность того, что из 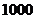 посеянных семян взойдут
посеянных семян взойдут 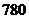 .
.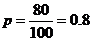 . Количество посеянных семян (общее количество испытаний)
. Количество посеянных семян (общее количество испытаний) 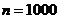 . Т.к.
. Т.к. 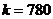 ;
; 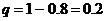 .
.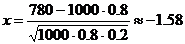 .
.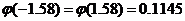 .
.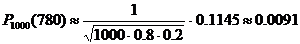 .
.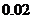 . Найти вероятность того, что из
. Найти вероятность того, что из 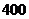 произведенных станком изделий:
произведенных станком изделий: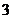 бракованных;
бракованных;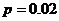 . Общее количество изготовленных изделий (общее количество испытаний)
. Общее количество изготовленных изделий (общее количество испытаний) 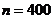 . Т.к.
. Т.к. 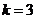 ;
;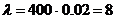 .
.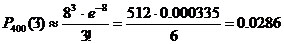 .
.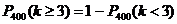 .
.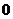 бракованных деталей, или
бракованных деталей, или  бракованная деталь, или
бракованная деталь, или 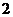 бракованных детали.
бракованных детали.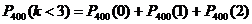 .
.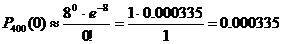 ;
;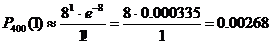 ;
;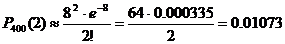 ;
;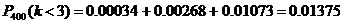 .
.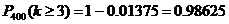 .
.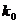 , для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события
, для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события 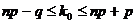
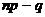 - целое число, то существуют два значения наивероятнейшего числа, а именно:
- целое число, то существуют два значения наивероятнейшего числа, а именно: 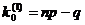 и
и 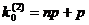 ;
;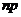 - целое число, то существует одно наивероятнейшее число, а именно:
- целое число, то существует одно наивероятнейшее число, а именно: 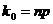 .
.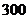 изделий, если вероятность качественного изделия равна
изделий, если вероятность качественного изделия равна 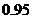 .
.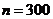 ,
, 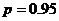 ; следовательно
; следовательно 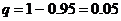 .
.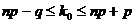
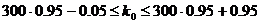 ;
;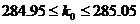 .
. .
. того, что при
того, что при  раз и не более
раз и не более 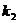 раз. Это можно сделать с помощью интегральной теоремы Лапласа:
раз. Это можно сделать с помощью интегральной теоремы Лапласа: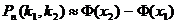 ,
,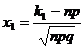 ,
, 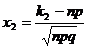 ;
;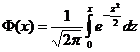 , Значения
, Значения 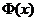 находят по таблице приложения 2. Функция
находят по таблице приложения 2. Функция 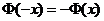 , таблица содержит значения функции
, таблица содержит значения функции 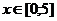 ; для
; для  можно принять
можно принять 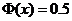 .
.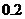 . Найти вероятность того, что среди
. Найти вероятность того, что среди 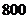 случайно отобранных деталей нестандартных окажется от
случайно отобранных деталей нестандартных окажется от 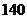 до
до 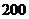 деталей.
деталей.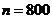 ,
, 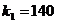 ,
, 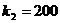 ,
, 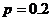 , следовательно
, следовательно 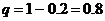 .
.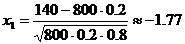 ;
;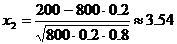 .
.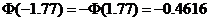 ;
;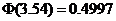 .
.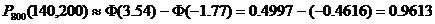 .
.


