
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Теорема может быть обобщена на любое конечное число совместных событий (например, для трех совместных событий):
Пример. Вероятность того, что стрелок при одном выстреле выбьет Решение. Обозначим События
Пример. В условиях предыдущего примера найти вероятность того, что при одном выстреле стрелок выбьет меньше Решение. Событие
Пример. Игральную кость подбросили один раз. Найти вероятность следующего события: на верхней грани появится либо четное число, либо число кратное трем. Решение. Обозначим
События
Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого. Пример. игральная кость брошена два раза. Вероятность появления « События Пример. В ящике
Несколько событий называют попарно независимыми, если каждые два из них независимы. Несколько событий называют независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий. Два события называют зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления другого события. Пример. В ящике Т.о. вероятность появления события
|
|||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.009 с.) |
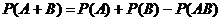 .
.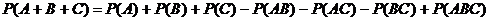 .
.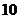 очков, равна
очков, равна 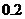 ; вероятность выбить
; вероятность выбить 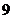 очков, равна
очков, равна 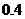 . Найти вероятность того, что при одном выстреле стрелок выбьет не менее
. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 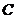 событие, состоящее в том, что при одном выстреле стрелок выбьет не менее
событие, состоящее в том, что при одном выстреле стрелок выбьет не менее 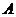 ), или
), или 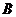 ), т.е.
), т.е. 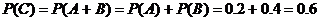 .
.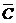 – при одном выстреле стрелок выбьет меньше
– при одном выстреле стрелок выбьет меньше 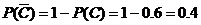 .
.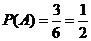 ; (т.к. общих исходов
; (т.к. общих исходов 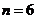 , благоприятствующих
, благоприятствующих 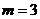
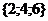 ).
).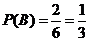 ; (
; (
 ).
).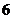 » появится и четное число, и кратное трем). Поэтому применяем теорему сложения вероятностей совместных событий:
» появится и четное число, и кратное трем). Поэтому применяем теорему сложения вероятностей совместных событий: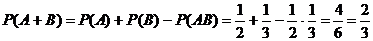 .
.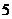 » при втором бросании (событие
» при втором бросании (событие  белых шара. Из ящика наудачу берут один шар. Очевидно, вероятность появления красного шара (событие
белых шара. Из ящика наудачу берут один шар. Очевидно, вероятность появления красного шара (событие 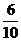 . Взятый шар возвращают в ящик и испытание повторяют. Вероятность появления красного шара при втором испытании (событие
. Взятый шар возвращают в ящик и испытание повторяют. Вероятность появления красного шара при втором испытании (событие 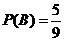 ; если же в первом испытании вынут белый шар, то вероятность
; если же в первом испытании вынут белый шар, то вероятность 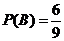 .
.


