
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Программа курса «теория вероятностей и математическая статистика»Стр 1 из 7Следующая ⇒
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Методические указания Предмет теории вероятностей
Всякое действие, явление, реализуемое при определенном комплексе условий называют испытанием. Результат испытания называют событием. Пример. Брошена монета – испытание; Появление герба – событие; События обозначают заглавными буквами латинского алфавита: А, В, … Наблюдаемые нами события можно подразделить на следующие три вида: q Достоверные; q Невозможные; q Случайные; Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S. Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Пример. Брошена игральная кость – испытание; Выпадение 4 х очков – событие; какое? - случайное; Выпадение не больше 6 и очков - событие; какое? – достоверное; Выпадение 10 и очков - событие; какое? – невозможное. Каждое случайное событие, в частности – выпадение герба, есть следствие действия очень многих случайных причин (сила, с которой брошена монета, форма монеты, сплав, из которого она сделана и др.). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, - она просто не в силах это сделать. По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий, независимо от их конкретной природы, подчиняется определенным закономерностям, а именно – вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей. Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений герба, если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монета бросается в одних и тех же условиях. Например, то, что застрахованный объект (дом, домашнее имущество и т.п.) будет уничтожен в результате стихийного бедствия, - дело случая, Чем же тогда страховые органы руководствуются в своей работе? Оказывается, что если о будущем определенного застрахованного объекта сказать ничего нельзя, то о состоянии большого их числа можно почти наверняка сказать многое. Виды случайных событий
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Пример. Монета брошена 1 раз. События: А – выпал герб и В – выпала решка несовместные. Брошена игральная кость. События: А – выпала 1, В – выпала 2, С – выпала 3 несовместные. События называют совместными, если появление одного из них не исключает появление других событий в одном и том же испытании. Пример. Брошена игральная кость. События: А – выпала 4, событие В – выпало четное число совместные. События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Пример. Стрелок произвел выстрел по цели. События: А – попадание в цель, В – промах единственно возможные в данном испытании. Событияназывают равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие. Пример. Брошена игральная кость. Равновозможные события: А – выпала 3 и В – выпала 5; или С – выпало четное число и Д – выпало нечетное число очков. Совокупность всех единственно возможных событий испытания называют полная группа событий. Пример. Стрелок произвел 2 выстрела. Полная группа событий:
Событие Событие Событие Противоположными называют два единственно возможных события образующих полную группу событий. Обозначение: Пример. Монета брошена 1 раз. События: Брошена игральная кость. События: События:
Операции над событиями
Суммой конечного числа событий называют новое событие, состоящее в наступлении хотя бы одного из них. (Суммой событий А и В называют событие состоящее в появлении или события А или события В, или обоих событий.); Логический принцип: или – или. Обозначение: А+В Пример. Событие А – попадание в круг, а событие В – попадание в квадрат; Тогда их сумма А+В заключается в попадании или в круг или в квадрат
Произведением конечного числа событий называют новое событие, состоящее в том, что произойдут все эти события. (Произведением двух событий А и В называют событие, состоящее и в появлении события А и в появлении события В). Логический принцип и – и. Обозначение: АВ Пример. Событие А – попадание в круг, а событие В – попадание в квадрат; Тогда их произведение АВ заключается в попадании в общую часть круга и квадрата.
Геометрическая вероятность
Геометрическое определение вероятности появилось, благодаря попытке отказаться от конечности m и n. Пусть на плоскости имеется некоторая область G и в ней содержится другая область g. Требуется найти вероятность того, что точка, взятая наудачу в области G, попадет в область g. При этом выражению «точка, взятая наудачу в области G» придается следующий смысл: эта точка может попасть в любую точку области G. Вероятность попадания точки в какую либо область G пропорциональна мере (mes) этой части (длине, площади, объему и т.д.) и не зависит от ее расположения и формы:
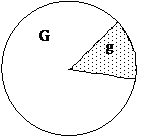
(геометрическое определение вероятности). Пример. Круглый диск радиуса R разбит на два сектора. Длина дуги одного из них (заштрихованного) равна радиусу R. По быстро вращающемуся диску произведен выстрел. Найти вероятность попадания в этот сектор. Решение. Событие А – попадание в сектор. В данном случае, в качестве меры выступает площадь;
площадь кругового сектора соответствующего центральному углу в длина дуги, соответствующей центральному углу в По условию:
Т.о.
Пример. (задача о встрече). Два студента А и В условились встретится в определенном месте во время перерыва между 13ч и 13ч 50мин. Пришедший первым ждет другого в течение 10 мин, после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанных 50мин. может произойти наудачу и моменты прихода неизвестны.
Для того чтобы они встретились, необходимо и достаточно, чтобы Изобразим x и y как декартовы координаты на плоскости, а в качестве масштаба выберем 1 минуту. Всевозможные исходы изобразятся точками квадрата со стороной 50:
Исходы, благоприятствующие встрече, - точками заштрихованной области.
Откуда
Аксиомы теории вероятностей
Аксиома 1. Каждому событию Аксиома 2. Вероятность достоверного события Аксиома 3. Вероятность суммы двух несовместных событий равна сумме их вероятностей. Аксиома 3*. Вероятность суммы конечного или бесконечного множества несовместных событий равна сумме их вероятностей:
Элементы комбинаторики
Формулы комбинаторики составляют теоретическую базу при использовании классического определения вероятности, которое в прикладных задачах играет большую роль. В зависимости от правил составления можно выделить три типа комбинаций: q Перестановки; q Размещения; q Сочетания; I. Перестановки. Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называют перестановками. Обозначаются символом
Пример. В соревновании участвовало 4 команды, сколько существует вариантов распределить места между ними. Решение. Количество вариантов распределения четырех команд по местам – равно числу перестановок из четырех элементов: Пример. В ящике пять одинаковых пронумерованных кубиков. Наудачу по одному извлекают все кубики из ящика. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке. Решение. Обозначим Благоприятствует событию Общее число возможных исходов – количество комбинаций из Искомая вероятность: Размещения Комбинации из n элементовпо k элементов, которые отличаются друг от друга или самими элементами, илипорядком элементов называют размещениями. Обозначаются символом
Пример. Сколько существует вариантов размещения Решение. Необходимо просчитать число возможных комбинаций извлеченных из
Пример. Из пяти карточек с буквами О, П, Р, С, Т наугад одну за другой выбирают три и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «ТОР»? Решение. Обозначим Благоприятствует событию Общее число возможных исходов – равно числу способов, которыми можно отобрать
Искомая вероятность:
Сочетания Сочетаниями называют все возможные комбинации из n элементовпо k элементов, которые отличаются друг от друга по крайней мере хотя бы одним элементом. Обозначаются символом
Пример. Сколькими способами можно выбрать Решение. Необходимо просчитать число возможных комбинаций извлеченных из 30 элементов и включающих по
Пример. В урне Решение. Обозначим Всего в урне Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь
Число исходов благоприятствующих событию
Искомая вероятность равна:
Пример. В ящике имеется Решение. Обозначим Обще число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь
Подсчитаем число исходов, благоприятствующих событию
Искомая вероятность:
В общем случае, для решения задач типа: В партии из
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Программа курса «теория вероятностей и математическая статистика» Раздел I. Теория вероятностей. Тема 1. Основные понятия теории вероятностей. Предмет курса. Предмет курса, его содержание. Роль и место курса как теоретической базы вероятностно - статистического моделирования, основ курсов "Математическое программирование", "Эконометрия", "Экономический риск и методы его измерения" и др. Классификация событий: достоверные, невозможные, случайные. Понятие Элементарной и сложной случайных событий, простор элементарных событий; операции над событиями. Классическое определение вероятности случайного события. Элементы комбинаторики в теории вероятностей и следствия из них; геометрическая вероятность, статистическая вероятность. Тема 2. Зависимые и независимые случайные события. Основные формулы умножения и сложения вероятностей. Понятия зависимой и независимой случайных событий. Условная вероятность и ее особенности. Формулы умножения вероятностей для зависимых и независимых случайных событий. Использование формул умножения вероятностей для оценки надежности систем. Формула полной вероятности. Формула Бейеса. Тема 3. Повторные независимые испытания по схеме Бернулли. Определение повторных независимых испытаний. Формула Бернулли для вычисления вероятности и наивероятнейшего числа. Асимптотические формулы для формулы Бернулли (локальная и интегральная теоремы Муавра - Лапласа). Использование интегральной теоремы. Формула Пуассона для маловероятных случайных событий. Тема 4. Одномерные случайные величины и их характеристики. Определение случайной величины. Дискретные и непрерывные случайные величины и их законы распределения. Функция распределения вероятностей, ее свойства. Числовые характеристики с.в.: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода, медиана, начальные и центральные моменты, асимметрия и эксцесс. Числовые характеристики среднего арифметического n независимых с.в. Тема 5. Многомерные случайные величины и их свойства. Определение многомерной с.в. и ее закон распределения. Система двух дискретных с.в., числовые характеристики системы, корреляционный момент, коэффициент корреляции и его свойства. Функция распределения вероятностей, ее свойства. Числовые характеристики системы двух непрерывных с.в. Условные законы распределения и их числовые характеристики. Определение корреляционной зависимости. Система n с.в., числовые характеристики системы, корреляционная матрица, нормированная корреляционная матрица. Тема 6. Функции случайных величин. Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей для функции двух случайных аргументов. Тема 7. Основные законы распределения целочисленных случайных величин. Определение целочисленной с.в. Биноминальный, пуассоновский, геометрический и равномерный законы распределения, функции и числовые характеристики для этих законов. Гипергеометрический закон. Тема 8. Основные законы распределения непрерывных случайных величин. Определение характеристической функции и ее использование в теории вероятностей. Нормальный закон распределения и его значение в теории вероятностей. Логарифмический нормальный закон. Гамма - распределение. Экспоненциальный закон и его использование в теории надежности, теории очередей. Распределение Вейбула. Равномерный закон. Распределение Тема 9. Предельные теоремы теории вероятностей. Неравенство Чебышева и его значение. Теорема Чебышева. Теорема Бернулли. Центральная предельная теорема теории вероятностей (теорема Ляпунова) и ее использование в математической статистике. Тема 10. Элементы теории случайных процессов. Определение случайного процесса и классификация случайных процессов. Законы распределения и основные характеристики. Поток событий и свойства. Поток событий Пальма. Пуассоновский поток и его свойства. Формула Пуассона для наипростейшего потока (потока Пуассона). Поток Эрланга. Марковские процессы. Цепи Маркова с дискретными состояниями. Однородные Марковские цепи и их классификация. Стационарные вероятности для регулярных цепей Маркова. Использование однородных цепей Маркова для оценки эффективности функционирования систем. Элементы теории массового обслуживания (теории очередей). Математическая модель для наипростейшей системы обслуживания. Раздел II. Математическая статистика. Тема 11. Элементы математической статистики. Выборочный метод. Генеральная и выборочная совокупности. Статистическое распределение выборки. Гистограмма и полигон статистических распределений. Числовые характеристики: выборочная средняя, дисперсия выборки, среднее квадратичное отклонение, мода и медиана, для дискретных и интервальных статистических распределений выборки, эмпирические начальные и центральные моменты, асимметрия и эксцесс. Тема 12. Статистические оценки параметров генеральной совокупности. Статистические гипотезы. Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Точечные несмещенные статистические оценки для генеральной средней и генеральной дисперсии, исправленная дисперсия. Интервальные статистические оценки. Точность и надежность оценки, определение доверительного интервала. Построение доверительных интервалов для генеральной средней с известным и неизвестным Тема 13. Элементы дисперсионного анализа. Модель эксперимента. Однофакторный анализ. Таблица результатов наблюдений. Общая дисперсия, межгрупповая и внутригрупповая дисперсии. Оценки дисперсий. Общий метод проверки влияния фактора на признак способом сравнения дисперсий. Понятие о двухфакторном дисперсионном анализе. Тема 14. Элементы теории регрессии и корреляции. Функциональная, статистическая и корреляционная зависимости. Уравнение парной регрессии. Свойства статистических оценок параметров парной функции регрессии. Выборочный коэффициент корреляции и его свойства. Доверительный интервал для линии регрессии. Коэффициент детерминации. Множественная регрессия, определение статистических оценок для параметров линейной множественной функции регрессии. Коэффициент корреляции и его свойства. Нелинейная регрессия. Определение статистических оценок для нелинейной функции регрессии. Методические указания Предмет теории вероятностей
Всякое действие, явление, реализуемое при определенном комплексе условий называют испытанием. Результат испытания называют событием. Пример. Брошена монета – испытание; Появление герба – событие; События обозначают заглавными буквами латинского алфавита: А, В, … Наблюдаемые нами события можно подразделить на следующие три вида: q Достоверные; q Невозможные; q Случайные; Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S. Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Пример. Брошена игральная кость – испытание; Выпадение 4 х очков – событие; какое? - случайное; Выпадение не больше 6 и очков - событие; какое? – достоверное; Выпадение 10 и очков - событие; какое? – невозможное. Каждое случайное событие, в частности – выпадение герба, есть следствие действия очень многих случайных причин (сила, с которой брошена монета, форма монеты, сплав, из которого она сделана и др.). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, - она просто не в силах это сделать. По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий, независимо от их конкретной природы, подчиняется определенным закономерностям, а именно – вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей. Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений герба, если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монета бросается в одних и тех же условиях. Например, то, что застрахованный объект (дом, домашнее имущество и т.п.) будет уничтожен в результате стихийного бедствия, - дело случая, Чем же тогда страховые органы руководствуются в своей работе? Оказывается, что если о будущем определенного застрахованного объекта сказать ничего нельзя, то о состоянии большого их числа можно почти наверняка сказать многое. Виды случайных событий
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Пример. Монета брошена 1 раз. События: А – выпал герб и В – выпала решка несовместные. Брошена игральная кость. События: А – выпала 1, В – выпала 2, С – выпала 3 несовместные. События называют совместными, если появление одного из них не исключает появление других событий в одном и том же испытании. Пример. Брошена игральная кость. События: А – выпала 4, событие В – выпало четное число совместные. События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Пример. Стрелок произвел выстрел по цели. События: А – попадание в цель, В – промах единственно возможные в данном испытании. Событияназывают равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие. Пример. Брошена игральная кость. Равновозможные события: А – выпала 3 и В – выпала 5; или С – выпало четное число и Д – выпало нечетное число очков. Совокупность всех единственно возможных событий испытания называют полная группа событий. Пример. Стрелок произвел 2 выстрела. Полная группа событий: Событие Событие Событие Противоположными называют два единственно возможных события образующих полную группу событий. Обозначение: Пример. Монета брошена 1 раз. События: Брошена игральная кость. События: События:
Операции над событиями
Суммой конечного числа событий называют новое событие, состоящее в наступлении хотя бы одного из них. (Суммой событий А и В называют событие состоящее в появлении или события А или события В, или обоих событий.); Логический принцип: или – или. Обозначение: А+В Пример. Событие А – попадание в круг, а событие В – попадание в квадрат; Тогда их сумма А+В заключается в попадании или в круг или в квадрат
Произведением конечного числа событий называют новое событие, состоящее в том, что произойдут все эти события. (Произведением двух событий А и В называют событие, состоящее и в появлении события А и в появлении события В). Логический принцип и – и. Обозначение: АВ Пример. Событие А – попадание в круг, а событие В – попадание в квадрат; Тогда их произведение АВ заключается в попадании в общую часть круга и квадрата.
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.205.123 (0.168 с.) |
 ; где
; где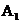 - промах;
- промах;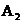 - одно попадание;
- одно попадание;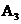 - два попадания;
- два попадания;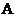 и
и 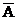 ;
;

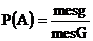 ;
;
 , где
, где 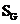 - площадь круга;
- площадь круга; 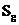 - площадь сектора.
- площадь сектора. ;
;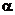 радиан:
радиан: 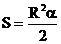 ;
; ;
;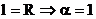 рад.
рад.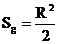 .
. .
. Решение. Обозначим момент прихода студента А через x, а студента В через y.
Решение. Обозначим момент прихода студента А через x, а студента В через y. .
.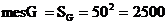 ;
;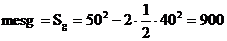 ;
;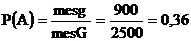 .
. , удовлетворяющее условию
, удовлетворяющее условию 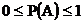 , и называемое его вероятностью.
, и называемое его вероятностью.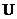 равна единице.
равна единице.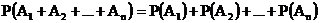 .
.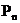 ;
;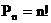 ;
; .
.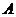 событие, состоящее в том, что номера извлеченных кубиков появятся в возрастающем порядке.
событие, состоящее в том, что номера извлеченных кубиков появятся в возрастающем порядке.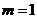 (из всех возможных комбинаций номеров только одна с порядком возрастания номеров).
(из всех возможных комбинаций номеров только одна с порядком возрастания номеров).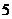 номеров,
номеров,  .
.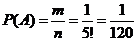 .
.
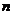 - количество всех имеющихся элементов;
- количество всех имеющихся элементов;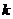 – количество элементов в каждой комбинации;
– количество элементов в каждой комбинации;  .
. ;
;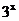 призовых мест, если в розыгрыше участвуют
призовых мест, если в розыгрыше участвуют  команд?
команд?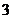 элемента (причем {I–«Таврия», II–«Динамо», III–«Спартак»} и {I–«Динамо», II–«Таврия», III–«Спартак»}– различные комбинации). Используем число размещений из
элемента (причем {I–«Таврия», II–«Динамо», III–«Спартак»} и {I–«Динамо», II–«Таврия», III–«Спартак»}– различные комбинации). Используем число размещений из 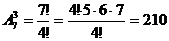 .
.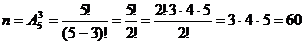 .
.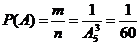 .
.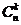
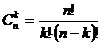 ;
;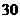 человек.
человек.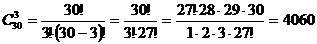 .
. красных шара. Из урны наудачу извлекают
красных шара. Из урны наудачу извлекают 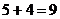 шаров.
шаров.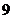 :
: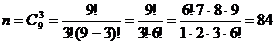 .
.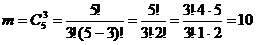 .
. .
.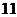 одинаковых шаров. Причем
одинаковых шаров. Причем 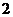 синих.
синих. .
. способами; при этом остальные
способами; при этом остальные 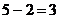 шара должны быть белыми, взять же
шара должны быть белыми, взять же  способами. Следовательно, число благоприятствующих исходов равно:
способами. Следовательно, число благоприятствующих исходов равно: .
.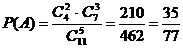 .
.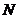 деталей имеется
деталей имеется 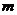 деталей. Найти вероятность того, что среди отобранных деталей ровно
деталей. Найти вероятность того, что среди отобранных деталей ровно  .
.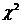 . Распределение
. Распределение  . Распределение Стьюдента. Распределение Фишера.
. Распределение Стьюдента. Распределение Фишера.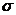 . Построение доверительных интервалов для генеральной дисперсии и генерального среднего квадратичного отклонения. Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная. Ошибки первого и второго рода. Статистический критерий. Критическая область, область принятия нулевой гипотезы, критическая точка. Методика построения правосторонней, левосторонней и двусторонней критических областей. Проверка правдивости нулевой гипотезы нормального закона распределения. Признаки генеральной совокупности. Проверка статистических гипотез про равенство двух генеральных средних и двух дисперсий, признаки которых имеют нормальные законы распределения. Эмпирическая и теоретическая частоты. Критерий согласия Пирсона. Критерий согласия Смирнова.
. Построение доверительных интервалов для генеральной дисперсии и генерального среднего квадратичного отклонения. Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная. Ошибки первого и второго рода. Статистический критерий. Критическая область, область принятия нулевой гипотезы, критическая точка. Методика построения правосторонней, левосторонней и двусторонней критических областей. Проверка правдивости нулевой гипотезы нормального закона распределения. Признаки генеральной совокупности. Проверка статистических гипотез про равенство двух генеральных средних и двух дисперсий, признаки которых имеют нормальные законы распределения. Эмпирическая и теоретическая частоты. Критерий согласия Пирсона. Критерий согласия Смирнова.


