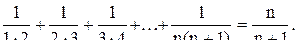Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод математической индукции.⇐ ПредыдущаяСтр 16 из 16
Нематематическая индукция играет существенную роль в математическом исследовании. Иса й Шур Всякое рассуждение, содержащее переход от частных рассуждений к общему, называется индукцией. Рассмотрим некоторые примеры рассуждения по индукции. Так, значения многочлена при ных чисел равна квадрату от числа взятых нечетных чисел. Верен ли этот вывод для любого числа взятых нечетных чисел? Чтобы в этом убедиться, поступим слдующим образом. Предположим, что данное утверждение верно для случая, когда число взятых нечетных чисел равно n, т.е. что утверждение
1)что это утверждение верно для Пример 1. Доказать, что сумма S(n) первых n членов натурального ряда равна Решение. При Пример 2. Доказать, что сумма S(n) квадратов первых n членов натурального ряда равна Решение. При Пусть эта формула верна, тогда: Пример 3. Доказать, что сумма S внутренних углов выпуклого n-угольника равна Решение. Рассмотрим выпуклый 6-угольник. Возьмем внутри него произвольную точку О и соединим ее с вершинами.Таким образом, мы разобьем этот многоугольник на 6 треугольников. Очевидно, сумма внутренних углов этого шестиугольника будет равна
Дом
дом математической индукции. При Пример 4. Доказать, что для арифметической пргрессии Решение. Докажем первую формулу.Очевидно,она верна при n=1.
Пусть формула верна, тогда Пример 5. Доказать, что для геометрической пргрессии Решение. Первую формулу мы предлагаем читателю доказать самостоятельно. Докажем вторую формулу. При Пример 6. Доказать неравенство Бернулли Решение. 1) Если 2) Если неравенство верно для n, то Пример 7. Доказать, что Решение. При 1) Если формула Пример 8. Используя метод математической индукции, доказать, что для Решение. При
Пример 8. Доказать формулу бинома Ньютона [5]
так как по предположению формула с показателем n верна. Выделяем из первой суммы член, получаемый при
Значит, формула верна и с показателем равным n+1. Условия математической индукции выполняются. Отсюда заключаем, что формула верна. Вопросы и задания для самопроверки. 1. Что называется индукцией? 2. Всегда ли верно заключение, сделанное по индукции? От чего зависит справедливость заключения по индукции? 3. Сформулировать метод математической индукции. 4. Обосновать необходимость выполнения двух условий 1) и 2) в методе математической индукции. 5. В каких случаях применяют метод математической индукции?
6. Вывести формулу разложения для разности 7. Вывести формулу для суммы n первых членов геометрической и арифметической прогрессии. 8. Вывести формулу для общего члена геометрической и арифметической прогрессии. 9. Доказать формулу бинома Ньютона. 10. Доказать, что 11. С помощью формулы бинома Ньютона вывести формулу Упражнения. 1. Доказать, что 2. Доказать, что 3. Верно ли неравенство 4. Докажите, что неравенство 5. Доказать, что 6. На сколько треугольников может быть разбит своими непересекающимися диагоналями n-угольник (не обязательно выпуклый)? Ответ:
Л и т е р а т у р а.
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.214 (0.028 с.) |
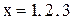 равны соответственно 41, 43, 47 и являются простыми числами,т.е. числами, которые делятся только на единицу и на себя нацело. Но отсюда еще не следует, что значения этого многочлена будут простыми числами при любом целом положительном значении х. Например, при
равны соответственно 41, 43, 47 и являются простыми числами,т.е. числами, которые делятся только на единицу и на себя нацело. Но отсюда еще не следует, что значения этого многочлена будут простыми числами при любом целом положительном значении х. Например, при  значение этого многочлена равно
значение этого многочлена равно 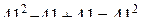 и уже не является простым числом. Приведем еще один пример. Выдающийся немецкий математик Лейбниц доказал, что при всяком целом положительном n выражение
и уже не является простым числом. Приведем еще один пример. Выдающийся немецкий математик Лейбниц доказал, что при всяком целом положительном n выражение 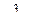 делится на 3, выражение
делится на 3, выражение 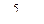 делится на 5, а выражение
делится на 5, а выражение 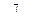 делится на 7. Из этих частных случаев он сделал общий вывод о том, что всякое выражение вида
делится на 7. Из этих частных случаев он сделал общий вывод о том, что всякое выражение вида  , где k – целое положительное нечетное число, делится на k, и сам же заметил, что число
, где k – целое положительное нечетное число, делится на k, и сам же заметил, что число 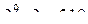 уже не делится на 9. Отсюда вытекает, что делать общие выводы по индукции (на основании конечного числа частных случаев!) нужно с большой осторожностью. Общий вывод можно сделать лишь тогда, когда рассмотрены все возможные частные случаи. Еще один пример. Найдем сумму S(n) первых n нечетных чисел натурального ряда. Очевидно,
уже не делится на 9. Отсюда вытекает, что делать общие выводы по индукции (на основании конечного числа частных случаев!) нужно с большой осторожностью. Общий вывод можно сделать лишь тогда, когда рассмотрены все возможные частные случаи. Еще один пример. Найдем сумму S(n) первых n нечетных чисел натурального ряда. Очевидно, 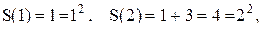 S(3)
S(3) 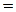
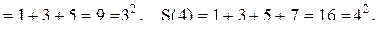 Мы замечаем, что сумма нечет
Мы замечаем, что сумма нечет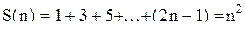 верно. Рассмотрим теперь сумму n+1 первых нечетных чисел
верно. Рассмотрим теперь сумму n+1 первых нечетных чисел 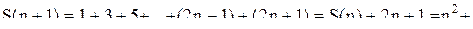
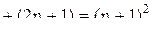 Оказалось, что и сумма S(n+1) первых нечетных чисел равна квадрату от их числа. Следовательно, из того, что утверждение верно для n=1 (мы это проверили), вытекает, что оно верно и для
Оказалось, что и сумма S(n+1) первых нечетных чисел равна квадрату от их числа. Следовательно, из того, что утверждение верно для n=1 (мы это проверили), вытекает, что оно верно и для  , а так как оно верно для
, а так как оно верно для  то оно верно и для
то оно верно и для 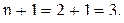 и т.д.. И мы, таким образом, проверяем сделанное заключение для
и т.д.. И мы, таким образом, проверяем сделанное заключение для  охватывая все возможные случаи. На этом примере мы показали, как незначительно изменив правило, названное индукцией, получить строгий метод доказательства, называемый методомматематической индукции. Сущность его заключается в следующем. Чтобы доказать, что некоторое утверждение верно для любого натурального числа n, начиная с no, достаточно доказать:
охватывая все возможные случаи. На этом примере мы показали, как незначительно изменив правило, названное индукцией, получить строгий метод доказательства, называемый методомматематической индукции. Сущность его заключается в следующем. Чтобы доказать, что некоторое утверждение верно для любого натурального числа n, начиная с no, достаточно доказать: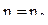 ;
;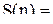
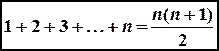
 имеем
имеем 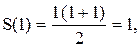 и условие 1) метода математической индукции верно. Предположим, что формула верна. Тогда:
и условие 1) метода математической индукции верно. Предположим, что формула верна. Тогда: 
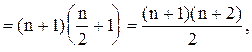 и условие 2) выполнено. Следовательно, формула верна для любого натурального числа n. Так, например,
и условие 2) выполнено. Следовательно, формула верна для любого натурального числа n. Так, например, 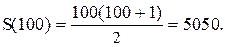

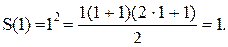
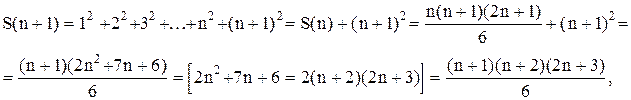 и, следовательно, формула верна для любого натурального числа n. Например,
и, следовательно, формула верна для любого натурального числа n. Например, 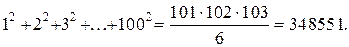
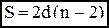
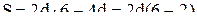 (мы здесь вычли сумму углов с вершиной в точке О). Если взять 8-угольник, то рассуждая аналогично, получим что
(мы здесь вычли сумму углов с вершиной в точке О). Если взять 8-угольник, то рассуждая аналогично, получим что 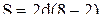 Легко заметить общую закономерность, что
Легко заметить общую закономерность, что 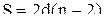 Чтобы убедиться в достоверности вывода воспользуемся мето
Чтобы убедиться в достоверности вывода воспользуемся мето 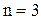 мы будем иметь треугольник, и
мы будем иметь треугольник, и  , что справедливо. Пусть формула верна. Рассмотрим (n+1)-угольник, который разобъем на (n+1) треугольников. Сумма его внутренних углов равна:
, что справедливо. Пусть формула верна. Рассмотрим (n+1)-угольник, который разобъем на (n+1) треугольников. Сумма его внутренних углов равна: 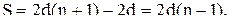 т.е. формула верна при n+1. Значит, условия 1) и 2) выполнены, и утверждение верно.Заметим,что сделанный вывод верен для любого многоугольника.
т.е. формула верна при n+1. Значит, условия 1) и 2) выполнены, и утверждение верно.Заметим,что сделанный вывод верен для любого многоугольника. верны формулы
верны формулы 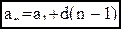 ,
, 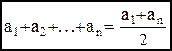
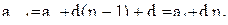 и она верна при n+1. Выполнены условия метода математической индукции, что позволяет утверждать справедливость формулы для вида общего члена арифметической прогрессии.. Доказательство второй формулы мы оставляем читателю.
и она верна при n+1. Выполнены условия метода математической индукции, что позволяет утверждать справедливость формулы для вида общего члена арифметической прогрессии.. Доказательство второй формулы мы оставляем читателю.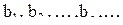 верны формулы
верны формулы 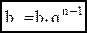 ,
, 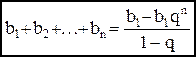
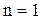 имеем
имеем 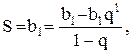 и формула верна. Если формула верна, то
и формула верна. Если формула верна, то 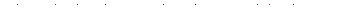

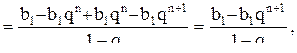 т.е. формула верна и при n+1. Следовательно, она верна для любого натурального числа n. Полагая
т.е. формула верна и при n+1. Следовательно, она верна для любого натурального числа n. Полагая 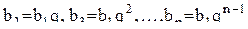 в формуле, получим, что
в формуле, получим, что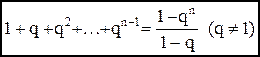 .
. 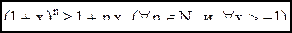
 , и неравенство верно.
, и неравенство верно.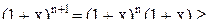 [так как
[так как 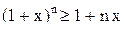 ]
] 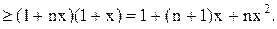 Отбрасывая неотрицательное число
Отбрасывая неотрицательное число  , получим
, получим 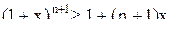 т.е. неравенство верно также и при n+1.
т.е. неравенство верно также и при n+1.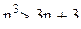 для
для 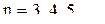
 это неравенство не выполнено, но уже при
это неравенство не выполнено, но уже при  оно верно, ибо
оно верно, ибо 
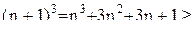
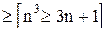
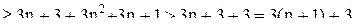 и условие 2) метода математической индукции выполнено.
и условие 2) метода математической индукции выполнено.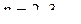 верна формула
верна формула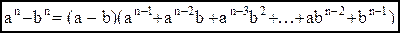
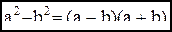 , и, значит, верна. Предположим, что формула верна. Тогда
, и, значит, верна. Предположим, что формула верна. Тогда
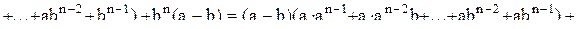
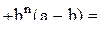
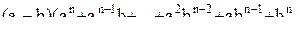 Следовательно, из того, что формула) верна при
Следовательно, из того, что формула) верна при  а из того, что она верна при
а из того, что она верна при 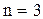 следует, что она верна при
следует, что она верна при 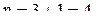 и т.д.. В частности,
и т.д.. В частности,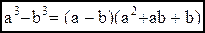 ,
, ,
,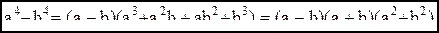 ,
,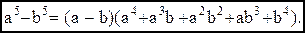
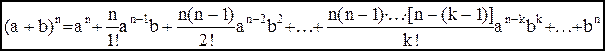 Эту формулу можно записать короче, если ввести обозначения
Эту формулу можно записать короче, если ввести обозначения 
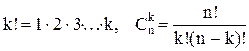 :
: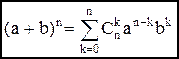 Решение. При
Решение. При 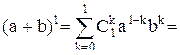
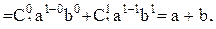 так как
так как  Она верна и при
Она верна и при 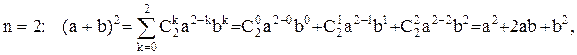 потому что
потому что 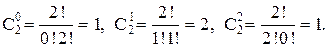 При
При 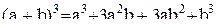 (проверьте!) Предположим теперь, следуя методу математической индукции, что формула справедлива с показателем равным n. Докажем, что отсюда вытекает справедливость ее с показателем n+1. Имеем:
(проверьте!) Предположим теперь, следуя методу математической индукции, что формула справедлива с показателем равным n. Докажем, что отсюда вытекает справедливость ее с показателем n+1. Имеем: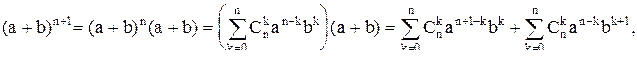
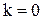 , а из второй суммы – член, соответствующий
, а из второй суммы – член, соответствующий 
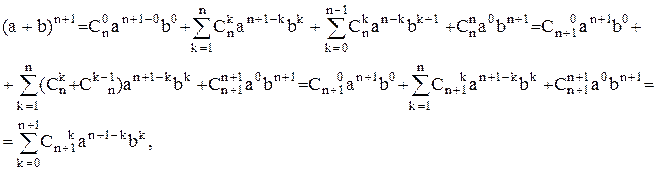 потому что
потому что  (проверьте!),
(проверьте!), 
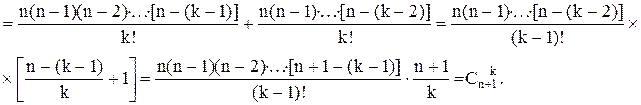
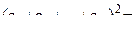
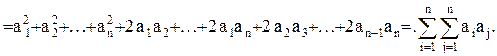
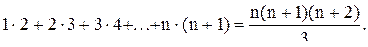
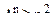 для
для 
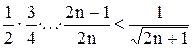 ?
? верно для
верно для