
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте и докажите свойства 1-6 модуля числа.
12. Верно ли, что 13. Верно ли, что 14. Доказать, что 15. Что меньше: расстояние между точками -3 и 15 или между точками -30 и -49? Найдите множество точек, расстояние от каждой из которых до точки -1 меньше 4 и больше 2. 18. Доказать, что 19. Верно ли, что Упражнения. 1.Решить неравенство Решение. Прежде всего находим точки, в которых обращаются в нуль выражения под знаком модуля: Решить уравнения: 1) 4) 7) 10) 13). 16) 19). 3. Решить неравенства и изобразить решения на числовой оси: 1) 5) 9) 4. Изобразить на координатной плоскости множества точек, координаты которых удовлетворяют следующим соотношениям: 1) 5) 9) 13) 16) 19) 22) 22) Ни одно человеческое исследование
не может называться истинной наукой,если оно не прошло через Математические доказательства. Леонардо да Винчи. Границы числовых множеств. Пусть Х – некоторое непустое числовое множество. Множество Х называется ограниченным сверху, если существует такое число М, что каждое число х из множества Х не превосходит числа М, т.е.
В этом случае Множество Х называется ограниченным, если оно ограничено и сверху и снизу, т.е. если существуют такие числа m и М, что каждое число х из множества Х удовлетворяяет неравенству
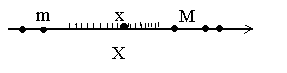
Например, множество Х=(0, 1] ограничено и сверху и снизу. Сверху оно ограничено любым числом Ограниченность множества Х равносильна существованию такого положительного числа С, что каждый элемент множества Х удовлетворяет неравенству В самом деле, если множество Х ограничено, то существуют такие числа m и M, что каждое число х из множества Х удовлетворяет неравенству
Всякое ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних) границ, а ограниченное множество имеет бесконечно много и верхних, и нижних границ одновременно. В самом деле, если М есть верхняя грань множества,то и всякое число М+произвольное положительное число также является верхней гранью(?), если же m есть нижняя грань множества,то и всякое число m- произвольное положительное число также является нижней гранью(?). Наименьшая из всех верхних границ ограниченного сверху множества Х называется точной верхней границей (гранью) множества Х и обозначается supX (sup – первые буквы латинского слова supremum – верхний); наибольшая из всех нижних границ ограниченного снизу множества Х называется точной нижней границей (гранью) множества Х и обозначается inf X (inf– первые буквы латинского слова infimum – нижний ). Возникает вопрос: всякое ли ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) границу? Ответ на эти вопросы дает следующая Теорема (о существовании точных границ). Всякое непустое ограниченное сверху (снизу) множество Х имеет (единственную!) точную верхнюю границу
Из теоремы следует, что всякое ограниченное множество имеет одну точную верхнюю и одну точную нижнюю границы. Например, Отметим важнейшие свойства точных границ числовых множеств. Пусть 1. 2. 3. если m – какая-либо нижняя граница множества Х, то Пусть. Тогда: 4. 5. 6. если М – какая-либо верхняя граница множества Х, то
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.214.56 (0.019 с.) |
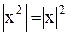 ? Докажите.
? Докажите.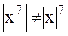 , если
, если 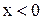 ?
?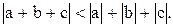
 , докажите.
, докажите.
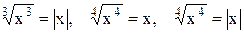 ?
?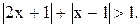
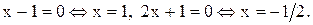 Точками
Точками  и
и 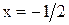 делим числовую прямую на три промежутка:
делим числовую прямую на три промежутка: 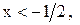
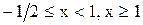 и рассматриваем исходное неравенство на каждом промежутке в отдельности. На первом промежутке (
и рассматриваем исходное неравенство на каждом промежутке в отдельности. На первом промежутке (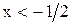 ) неравенство принимает вид
) неравенство принимает вид  так как
так как 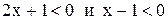 для
для 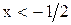 и, значит,
и, значит, 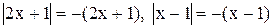 по определению модуля. Не все найденные нами решения (
по определению модуля. Не все найденные нами решения (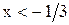 ) попадают в промежуток
) попадают в промежуток 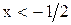 , для указанных промежутков (
, для указанных промежутков (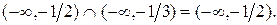 Следовательно, весь промежуток
Следовательно, весь промежуток 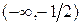 является решением исходного неравенства. Если же
является решением исходного неравенства. Если же 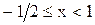 , то
, то 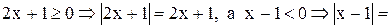
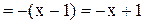 . Неравенство в этом случае примет вид:
. Неравенство в этом случае примет вид: 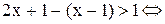
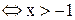 . Все точки промежутка
. Все точки промежутка 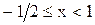 удовлетворяют неравенству
удовлетворяют неравенству 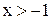 и, следовательно, являются решением исходного неравенства. На третьем промежутке (
и, следовательно, являются решением исходного неравенства. На третьем промежутке (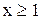 ) исходное неравенство равносильно системе
) исходное неравенство равносильно системе 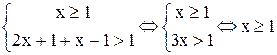 . Объединяя все найденные решения, получим решение исходного неравенства:
. Объединяя все найденные решения, получим решение исходного неравенства: 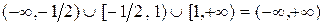 . Аналогично рассматриваются уравнения, содержащие неизвестную величину под знаком модуля.
. Аналогично рассматриваются уравнения, содержащие неизвестную величину под знаком модуля.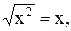 2)
2)  3)
3) 
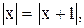 5)
5) 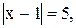 6)
6) 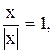
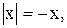 8)
8) 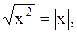 9)
9) 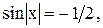
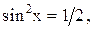 11)
11) 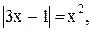 12)
12) 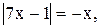
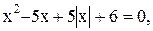 14)
14) 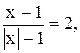 15)
15) 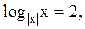
 17)
17) 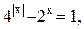 18)
18) 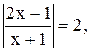
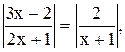 20)
20) 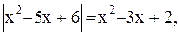 21)
21) 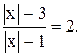
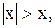 2)
2) 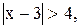 3)
3) 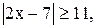 4)
4) 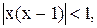
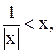 6)
6) 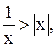 7)
7)  8)
8) 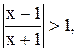
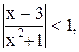 10)
10) 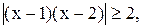 11)
11) 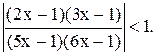
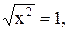 2)
2) 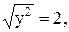 3)
3) 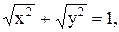 4)
4) 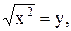
 6)
6) 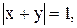 7)
7) 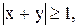 8)
8) 
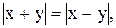 10)
10) 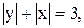 11)
11) 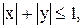 12)
12) 
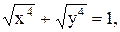 14)
14)  15)
15) 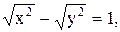
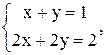 17)
17) 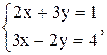 18)
18) 
 20)
20) 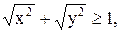 21)
21) 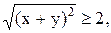
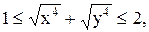 23)
23) 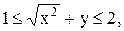 24)
24) 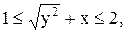
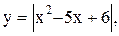 26
26 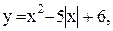 28)
28) 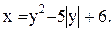
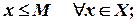 число М называется верхней границей (или гранью) множества Х.
число М называется верхней границей (или гранью) множества Х.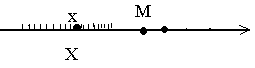 В этом случае все точки х из множества Х расположены слева от точки М. Так, множество Х={-1, -2, -3, -4,...} ограничено сверху любым числом
В этом случае все точки х из множества Х расположены слева от точки М. Так, множество Х={-1, -2, -3, -4,...} ограничено сверху любым числом 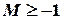 . Каждое такое число является верхней границей данного множества. Множество N ={1, 2, 3,...} не будет ограниченным сверху, так как для любого числа М, каким бы большим оно ни было, найдется целое положительное число из множества N большее М.
. Каждое такое число является верхней границей данного множества. Множество N ={1, 2, 3,...} не будет ограниченным сверху, так как для любого числа М, каким бы большим оно ни было, найдется целое положительное число из множества N большее М.
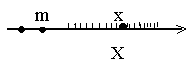 Множество Х называется ограниченным снизу, если существует такое число m, что каждое число х из множества Х не меньше числа m, т.е.
Множество Х называется ограниченным снизу, если существует такое число m, что каждое число х из множества Х не меньше числа m, т.е. 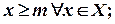 число m называется нижней границей (или гранью) множества Х.
число m называется нижней границей (или гранью) множества Х.
 в се точки х из множества Х расположены справа от точки m. Например, множество N ={1, 2, 3,... } ограничено снизу любым числом
в се точки х из множества Х расположены справа от точки m. Например, множество N ={1, 2, 3,... } ограничено снизу любым числом 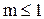 . Каждое такое число является нижней границей данного множества. Множество Х={-1, -2, -3, -4,...} не будет ограниченным снизу, так как для любого числа m, каким бы большим оно ни было, найдется целое отрицательное число из Х меньшее m.
. Каждое такое число является нижней границей данного множества. Множество Х={-1, -2, -3, -4,...} не будет ограниченным снизу, так как для любого числа m, каким бы большим оно ни было, найдется целое отрицательное число из Х меньшее m.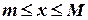 .
.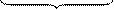
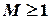 , а снизу – любым числом
, а снизу – любым числом 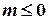 . Множество Z ={..., -1, 0, 1, 2,...} не является ограниченым ни снизу, ни сверху (почему?). Условимся считать пустое множество Æ ограниченным.
. Множество Z ={..., -1, 0, 1, 2,...} не является ограниченым ни снизу, ни сверху (почему?). Условимся считать пустое множество Æ ограниченным.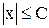 .
.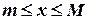 . Пусть С есть наибольшее из чисел
. Пусть С есть наибольшее из чисел 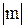 и
и 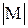 . Тогда, очевидно,, т.е.
. Тогда, очевидно,, т.е. 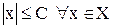 . И наоборот, если для любого
. И наоборот, если для любого 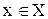 верно неравенство
верно неравенство 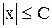 , то
, то 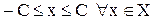 , т.е. множество Х ограничено (числом
, т.е. множество Х ограничено (числом 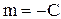 снизу и числом
снизу и числом 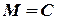 сверху).
сверху).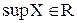 (точную нижнюю границу
(точную нижнюю границу 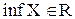 ).
).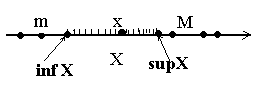
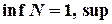
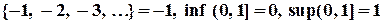 .
.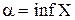 . Тогда:
. Тогда: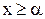 для каждого
для каждого 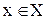 , ибо
, ибо 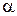 есть нижняя граница множества Х;
есть нижняя граница множества Х;
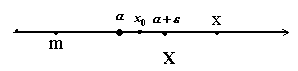 для любого
для любого 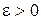 всегда найдется элемент
всегда найдется элемент  из Х такой, что
из Х такой, что 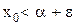 (в противном случае
(в противном случае 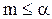 , ибо
, ибо 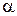 – наибольшая из всех нижних границ Х.
– наибольшая из всех нижних границ Х.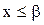 для каждого х из Х, ибо
для каждого х из Х, ибо 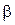 есть верхняя граница множества Х;
есть верхняя граница множества Х;
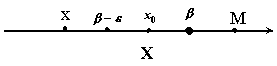 для любого
для любого 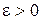 всегда существует элемент
всегда существует элемент 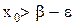 (в противном случае
(в противном случае 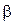 не было бы точной верхней границей множества Х, почему?);
не было бы точной верхней границей множества Х, почему?);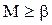 , ибо
, ибо  – наименьшая из всех верхних граней множества Х.
– наименьшая из всех верхних граней множества Х.


