
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совокупность элементов А называется подмножеством множества В, если все элементы совокупности А являются в то же время элементами множества В.
Записывают это так: А Ì В (А содержится в В), или В É А (В содержит А). Два множества А и В считаются равными (А=В), если они состоят из одних и тех же элементов. Множество называется пустым ( обозначают Æ), если оно не содержит ни одного элемента. Так, множество слонов в г.Жлобине есть пустое множество. Считается, что пустое множество содержится в любом множестве,т.е. Æ Ì А,где А-любое множество. Множество записывается в виде Числа 1, 2, 3, 4,... составляют множество натуральных чисел N={1, 2, 3, 4,... }. Все целые положительные и отрицательные числа и нуль образуют множество целых чисел Z= Заметим, что каждое рациональное число можно представить в виде бесконечной десятичной периодической дроби. Так, 1=0,999...=0,(9); 2=2,(0); 203/165=- 1,2(30). Положительные дроби были известны в Вавилоне и Египте. Полагают, что индийцы изобрели число нуль, а отрицательные рациональные числа были введены в Италии в эпоху Возрождения. Множество всех рациональных чисел обозначается буквой Q. Рациональные числа были введены для измерения отрезков. Долгое время считали, что любые два отрезка соизмеримы. Это значит, что если один отрезок принять за единицу измерения (масштаб), то длина другого выразится рациональным числом. Другими словами, если не сам единичный отрезок, то некоторая его часть (например, n -ая часть) откладывается m раз на измеряемом отрезке. Естественно, что его длина будет равна
всякое иррациональное число есть бесконечная непериодическая десятичная дробь. Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначается буквой R. Имеем Æ Ì N Ì Z Ì Q Ì R
Возьмем произвольную прямую и выберем на ней одно из двух направлений, которое будем называть положительным. Обозначим его стрелкой. Тогда другое направление будет отрицательным. За начало отсчета возьмем произвольную точку на прямой и обозначим ее буквой О. Произвольный отрезок ОЕ, длину которого будем считать равной 1, примем за масштаб измерений. Такая прямая называется числовой прямой
Пусть М - точка на числовой прямой. Поставим ей в соответствие положительное число х, которое выражает длину отрезка ОМ, если точка М находится справа от точки О, и число -х, если она находится слева от точки О на расстоянии х. Точке отсчета О поставим в соответствие число нуль. Таким образом, каждой точке М, взятой на числовой прямой, соответствует единственное действительное число х, которое называется абсциссой (или координатой) этой точки. И наоборот, каждому числу х из R соответствует единственная точка М, координата которой равна х. Записывают М(х). Установленное соответствие между точками числовой прямой и числами является взаимно однозначным. Поэтому между точками числовой оси и их координатами не делается различия. Говорят, что имеется точка М(х) или число х. Числовым множеством называется любая совокупность действительныхчисел. Примерами часто встречающихся числовых множеств являются конечные и бесконечные промежутки:
1. Отрезок [a,b] = {x | x Î R, a £ x £ b} с концами a и b.
2. Интервал (a, b) = { x | x Î R, a < x < b } с концами a и b.
3. Полуинтервалы [a,b) = {x | x Î R, a £ x<b}, (a,b] = {x | x Î R, a<x £ b}.
4. Полупрямые (- ¥,a] = {x | x Î R, - ¥ <x £ a}, [a,+ ¥) = {x | x Î R, a £ x<+ ¥ }. Открытые полупрямые (- ¥, a) = { x | x Î R, - ¥ < x < a }, (a,+ ¥) = { x | x Î R, a < x <+ ¥ }. 6. Числовая прямая (- ¥,+ ¥)=R. Множество может содержать как конечное число элементов, так и бесконечное. В первом случае множество называется конечным, во втором случае бесконечным. Так, множество государств на Земле конечно, а множество натуральных чисел N бесконечно.. Между двумя множествами установлено взаимно однозначное соответствие, если каждому элементу одного из этих множеств поставлен в соответствие единственный элемент другого множества, и наоборот. Из этого следует, что двум различным элементам одного из этих множеств соответствуют два различных элемента другого множества. Так, между натуральными числами и четными натуральными числами можно установить взаимно однозначное соответствие, ставя натуральному числу n в соответствие четное число 2 n, и наоборот.
Два множества называются эквивалентными, если между ними можно установить взаимно однозначное соответствие. Так множества N и Множество называется счетным, если оно эквивалентно множеству натуральных чисел.
Другими словами, множество счетно, если все его элементы можно пронумеровать. Так, множество всех целых чисел счетно (ниже числовой оси изображены целые числа, а сверху их номера)
Вопросы и задания для самопроверки.
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.153.224 (0.014 с.) |
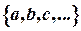 , если известны его элементы, и в виде
, если известны его элементы, и в виде 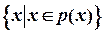 ,если х -его общий элемент,обладающийпризнаком р(х). Например,
,если х -его общий элемент,обладающийпризнаком р(х). Например, 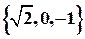 -множество, элементами которого являются числа
-множество, элементами которого являются числа  ;
; 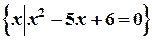 -множество,состоящее из корней квадратного уравнения х2-5х+6=0, т.е. оно совпадает с множеством
-множество,состоящее из корней квадратного уравнения х2-5х+6=0, т.е. оно совпадает с множеством 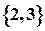 .
.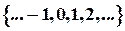 . Отношение двух целых чисел
. Отношение двух целых чисел  (n ¹ 0) называется рациональным числом.
(n ¹ 0) называется рациональным числом.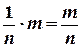 . Греческие математики из школы Пифагора [2] 2500 лет тому назад открыли несоизмеримые отрезки. Примером несоизмеримых отрезков может служить сторона квадрата и его диагональ. Пусть сторона квадрата выбрана за масштаб измерения и ее длина, по определению, равна 1. Если бы длина диагонали квадрата выражалась рациональным числом х, то было бы х2=2, что следует из теоремы Пифагора. Это же получим из того, что площадь “ большого ” квадрата в два раза больше площади “ малого ” квадрата, которая равна 1.Покажем, что х не может быть рациональным числом, и, следовательно, диагональ не имеет длины, выражаемой рациональным числом.
. Греческие математики из школы Пифагора [2] 2500 лет тому назад открыли несоизмеримые отрезки. Примером несоизмеримых отрезков может служить сторона квадрата и его диагональ. Пусть сторона квадрата выбрана за масштаб измерения и ее длина, по определению, равна 1. Если бы длина диагонали квадрата выражалась рациональным числом х, то было бы х2=2, что следует из теоремы Пифагора. Это же получим из того, что площадь “ большого ” квадрата в два раза больше площади “ малого ” квадрата, которая равна 1.Покажем, что х не может быть рациональным числом, и, следовательно, диагональ не имеет длины, выражаемой рациональным числом. Сначала заметим, что всякое целое число либо четное, т.е. делится на 2, либо нечетное, т.е. не делится на 2. Пусть m нечетное число, тогда m+1 четное число, т.е. m+1=2n. Отсюда m=2n-1, и m2 =(2n-1)(2n-1)=4n2-4n+1=4(n2-n)+1. Значит, m2 является нечетным числом, потому что 4(n2-n) четное число. Из сказанного вытекает, что m четное число, если m2 является четным числом. Пусть х является рациональным числом, т.е.
Сначала заметим, что всякое целое число либо четное, т.е. делится на 2, либо нечетное, т.е. не делится на 2. Пусть m нечетное число, тогда m+1 четное число, т.е. m+1=2n. Отсюда m=2n-1, и m2 =(2n-1)(2n-1)=4n2-4n+1=4(n2-n)+1. Значит, m2 является нечетным числом, потому что 4(n2-n) четное число. Из сказанного вытекает, что m четное число, если m2 является четным числом. Пусть х является рациональным числом, т.е. 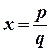 , причем p и q не являются одновременно четными числами, так как в противном случае множитель 2 в числителе и знаменателе можно сократить. Имеем x2=p2/q2=2 Û p2=2q2. Так как 2q2 четное число, то и p четное число по сделанному выше замечанию. Пусть p=2r. Тогда 4r2=2q2 Û 2r2=q2. Число 2r2 четное, и, следовательно, q четное число. Итак, p и q четные числа вопреки предположению.Согласно легенде, человек, объявивший о существовании несоизмеримых отрезков, был наказан богами, так как он раскрыл несовершенство мироздания, созданного богом. Греческие математики были потрясены открытием несоизмеримых отрезков, так как оно ставило под сомнение ранее доказанные теоремы о длинах отрезков и отношениях их длин. Возникшая трудность была разрешена Евдоксом [3], создавшим строгую теорию пропорций. В современной математике эта проблема решается введением новых чисел, которые называются иррациональными. С введением иррациональных чисел любые два отрезка становятся соизмеримыми, т.е. отношение их длин выражается рациональным или иррациональным числом. В нашем случае длина диагонали квадрата равна иррациональному числу. Это число открыл ученик Пифагора Чипас. Заметим, что
, причем p и q не являются одновременно четными числами, так как в противном случае множитель 2 в числителе и знаменателе можно сократить. Имеем x2=p2/q2=2 Û p2=2q2. Так как 2q2 четное число, то и p четное число по сделанному выше замечанию. Пусть p=2r. Тогда 4r2=2q2 Û 2r2=q2. Число 2r2 четное, и, следовательно, q четное число. Итак, p и q четные числа вопреки предположению.Согласно легенде, человек, объявивший о существовании несоизмеримых отрезков, был наказан богами, так как он раскрыл несовершенство мироздания, созданного богом. Греческие математики были потрясены открытием несоизмеримых отрезков, так как оно ставило под сомнение ранее доказанные теоремы о длинах отрезков и отношениях их длин. Возникшая трудность была разрешена Евдоксом [3], создавшим строгую теорию пропорций. В современной математике эта проблема решается введением новых чисел, которые называются иррациональными. С введением иррациональных чисел любые два отрезка становятся соизмеримыми, т.е. отношение их длин выражается рациональным или иррациональным числом. В нашем случае длина диагонали квадрата равна иррациональному числу. Это число открыл ученик Пифагора Чипас. Заметим, что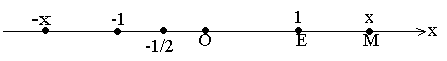



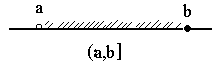
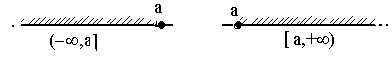
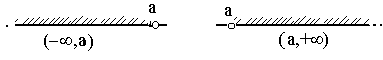
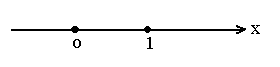
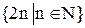 являются эквивалентными.
являются эквивалентными.



