
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Іі. Найпростіші висновки з аксіоматики.
Означення 1. Всяке кільце К відносно операції додавання, означеної в ньому, утворює адитивну абелеву групу – адитивну групу кільця К. Внаслідок цього всі властивості, які мають адитивні абелеві групи. Справедливі і у випадку довільного кільця К. Відзначимо деякі з них. Означення 2. Нулевий елемент кільця К є єдиним і всякий елемент кільця К має єдиний протилежний. Означення 3. Які б не були елементи a, b Означення 4. ( Аналогічно, як і для адитивних абелевих груп, вводиться поняття n-кратного елемента n а до а: а+а+...+а, n >0, na ={ 0, n =0, (n)(- a)=(- a)+(- a)+…+(- a), n <0. Нагадаємо, що n - кратний елемент nа задовольняє співвідношення: Означення 5. ( m (na)=(mn) a. Означення 6. Всяке кільце К відносно операції множення, означеної в ньому, утворює мультиплікативну півгрупу. Наявність асоціативного закону для множення дозволяє ввести поняття n -го степеня елемента а: ( Означення 7. Відзначимо ще 4 властивості, при доведені яких використовується дистрибутивність множення відносно додавання. Означення 8. ( На підставі означення досить показати, що ас+а (b -с) = ab. В справедливості останньої рівності пересвідчуємось, використовуючи аксіому 6) і означення різниці b -с: ас+а (b -с)= а (с +(b -с))= а b. Означення 9. ( Справді, який би не був елемент х а* 0= а (х +(-х))= а (х-х)= ах-ах = ах +(-ах)=0. Як відомо, в довільному полі і в кільці Z цілих чисел справедливе обернене твердження: ( У випадку довільного кільця це твердження, взагалі кажучи, невірне. Існують кільця,в яких із рівності а b =0 не випливає, що а або в дорівнюють 0. Наприклад, в кільці
Це зауваження дозволяє ввести нове поняття, поняття дільника нуля. Означення. Якщо для деяких елементів а, b В кільці М 2 дільниками нуля є, наприклад, матриці
Вивчення кілець, в яких є дільники 0, дещо ускладнюється. В подальшому ми будемо займатися вивченням тільки тих кілець, в яких нема дільників 0. Комутативне кільце, в якому нема дільників нуля, називається областю цілісності.
Означення 10. Перша рівність означає. Що елемент (-а) b має бути протилежним до а b, тобто, має виконуватись рівність: а b +(-а) b =0. Ця рівність легко випливає із аксіом 6) і 4) та властивості 9: а b + (-а) b = (а+ (-а)) b = 0 b =0. Аналогічно доводиться, що а(- b)=-а b. Справедливість останньої рівності легко виводиться із перших двох (-а)(- b)=-а(- b)=-(-а b)=а b, бо із рівності а+(-а)=0 в аксіомі 4) виходить, що (-а)+а=0, тобто елементом, протилежним до (-а) Означення 11. Якщо ненулевий елемент а Справді, додавання до обох частин рівності а а або в силу властивості a ( Оскільки елемент а не є дільником нуля, то Зауважимо, що скорочувати рівності на дільники нуля не можна. Справді, як легко пересвідчитись, в кільці М
в той час, як
ІІІ. Підкільце. Одним із важливих напрямків в теорії кілець є вивчення кілець підмножин кільця. Серед усіх підмножин кільця особливо виділяються ті підмножини, які самі є кільцями відносно операцій, означених в усьому кільці. Означення. Підмножина К Наступна теорема дозволяє спростити фактичну перевірку того, чи утворює певна підмножина кільця його підкільце. Теорема 1. Підмножина 1) ( 2) ( 3) ( Доведення. Якщо підмножина Якщо підмножина
Із умови 2 випливає,що для всякого а Приклади. 1. Підмножина Р усіх парних цілих чисел є підкільцем кільця Z цілих чисел. Справді, сума, добуток, парних чисел і число, протилежне до парного, є парними. Це означаєщо Р задовольняє умовам теореми 1, значить Р є пілкільцем кільця Z. 2. Множина Р усіх парних неперервних функцій утворює підкільце кільця С усіх неперервних функцій на [-1,1]. Дійсно, для довільних функцій f (x), g (x) (f+g)(x)= f (-x)+ g (-x)= f (x)+ g (x)=(f+g)(x), (fg)(x)= f (-x) g (-x)= f (x) g (x)=(fg)(x), (-f)(-x)= -f (-x)= -f (x)=(-f)(x). Отже, ( Тобто, множина Р на підставі теореми 1, є підкільцем кільця С. 3.Множина D Зауваження. Умова 2) у формулюванні теореми 1 може бути замінена умовою: 2′) ( Справді, якщо умова 2′) виконується, то для всякого елемента b а- b = а +(- b) Навпаки, якщо справджується умова 2′), то ( Бо 0=а-а і значить, належить Закінчемо параграф переліком деяких підкілець довільного підкільця. 1. Множина О={o}, яка складається тільки з одного нульового елемента кільця К, утворює, очевидно, підкільце кільця К. Це підкільце називають нульовим підкільцем К. 2. Кільце К є, очевидно, підкільцем самого себе. Підкільце О і К називають тривіальними підкільцями кільця К, а всі інші підкільця – нетривіальними або властними підкільцями. 3. Якщо Кα – деякі підкільця кільця К, то їх перетин Ко= Дійсно, якщо a Відомо, яку важливу роль в теоремі груп відіграють циклічні підгрупи (а), породжені елементом а. В наступному пункті побудоване підкільце, яке є аналогом циклічної підгрупи. 4. Нехай К - деяке кільце, а - елемент кільця К. Тоді множина Кα усіх можливих сум
де n1, Кα = Щоб показати, що множина Кα - підкільце кільця К, досить перевірити виконання 1.-3. Із теореми 1. В силу асоціативності додавання виконання умови 1. Очевидне, бо скінчених сумах можна довільно розставляти дужкиі, зокрема, їх опускати: (
1.Як відомо, одним із основних понять математики є поняття, функції, відображення. Це поняття вивчається і в математичному аналізі,і в геометрії,і в алгебрі. При вивченні алгебраїчних структур найбільший інтерес становлять ті відображення, які певним способом узгодженні із алгебраїчною структурою, що вивчається. В теорії груп такими відображеннями є гомоморфізми, тобто, такі ж відображення f групи G в групу
( В теорії кілець вивчаються відображення, які аналогічним способом узгоджені з алгебраїчними операціями, означеними в кільці. Такі відображення називаються кільцевими гомоморфізмами. Означення 1. Відображення f кільця К в кільце ( Перша з цих умов означає, що кільцевий гомоморфізм f в груповим гомоморфізмом адитивної групи кільця К в адитивну групу кільця 1. f (o)=0; 2.( Аналогічно, як і випадку груп, гомоморфізм f: K У зв’язку із властивостями 1. i 2. Виникає питання, чи не будуть аналогічні властивості справедливі відносно операцій множення. Виявляється, що будуть, але при деяких обмеженнях на кільця або на відображення f. Сформулюємо їх: 3. Якщо в кільці К існує 1 i f є епіморфізмом кільця К в кільці Справді, внаслідок сур’єктивності відображення f: ( Тоді ( ( Звідси виходить, що елемент f (1) відіграє роль одиниці в кільці 4.Якщо в кільці К існує І, кільце Дісно, ( і з другого боку, f(a)=f(a) f (a) [ f (1)- Оскільки в К нема дільників нуля і а можна підібрати так, щоб а є К ми включаємо тривіальний випадок: ( є таким, що f (1)= f ( Твердження випливає із рівностей: f (a) f ( f ( Для групового гомоморфізму вводять поняття ядрa Kerf і області значень Imf. Аналогічні поняття вводяться і для кільцевого гомоморфізму. Означення 2. Ядром гомоморфізму f: K
Ker f ={ Областю знаень або образом гомоморфізму f: K Im f ={ Як відомо, у випадку групового гомоморфізму f: G Приклад. Розглянемо кільце
і кільце
в якому операції задані так:
Відображення f є гомоморфізмом: Якщо
А+В= і значить f ( A+B)=( AB= f (AB)=( Очевидно, що Ker f = Im f = {a = ( ІІ. Серед гомоморфізмів особлива роль належить ізоморфізмам. Якщо існує ізоморфне відображення кільця К на кільце Теорема 1. Якщо кільце К ізоморфне множині М з двома алгебраїчними операціями – додавання та множення, то множина М теж є кільцем. Доведення. Нехай кільце К ізоморфне множині М, на якій означено операції додавання і множення. Нам треба довести, що множина М є кільцем. Оскільки на множині М операції вже означено, то залишається тільки показати, що ці операції задовольняють аксіоми кільця. Оскільки кільце К ізоморфне М, то відображення ізоморфне f: K → M. Відображення f зокрема є сур’єктивним і, значить: ( Тоді, в силу гомоморфності відображення f і справедливості аксіом кільця для операцій, означених на К, ми матимемо: (а′+ f (a+(b+c))=f (a)+f (b+c)=f (a)+(f (b)+ f (c))= а′+
Таким чином, операції, означені на множині М, задовольняють аксіоми 1),2), 5), і 6) означення кільця. Роль нулевого елемента в М виконує f (0): а′ протилежним елементом до елемента а′ Отже, множина М є кільцем. Як бачимо, ізоморфізм переносить алгебраїчні властивості з однієї множини на другу. При допомозі ізоморфізму можна розв’язати і питання про існування обернених елементів. Цим займемося в наступному пункті. ІІІ. Поле дробів області цілісності. Якщо кільце К є кільцем з одиницею, то деякі елементи цього кільця мають обернені до себе. Постараємося з’ясувати, для яких елементів кільця існують обернені елементи.Справді, якщо а — дільник нуля кільця К, тобто, існує такий елемент
Отже, шукати елементи, що мають обернені, треба серед недільників нуля. Виникає питання: чи кожен елемент, що не є дільником нуля, має обернений? Відповідь одержується, коли з цього погляду розглянути кільце Z цілих чисел. В кільці Z обернені елементи мають тільки 1 і -1. Інші числа обернених елементів не мають і в той же час вони не є дільниками нуля. Отже, не всі недільники нуля мають обернені елементи. Одначе, для кільця Z цілих чисел існує більш широке кільце — поле раціональних чисел, яке містить кільце Z і в якому кожне ненулеве ціле число має обернене число. Тоді можна поставити питання: чи не має місця аналогічна ситуація у випадку довільного кільця К? Виявляється, що має і це можна обґрунтувати ввівши поняття ізоморфного вкладення кільця в кільце.
Означення. Говорять, що кільце К ізоморфно вкладається в кільце K ′, якщо існує ізоморфне відображення кільця К на деяке підкільце K ′. Виявляється, що кожне кільце К можна ізоморфно вкласти в кільце K ′ Теорема 2. Всяка область цілісності К ізоморфно вкладається в поле Доведення. Щоб виробити підхід до доведення даної теореми, зауважимо, що поле раціональних чисел, яке містить в собі кільце цілих чисел і в якому кожне ненулеве ціле число має обернене, одержується із кільця Z шляхом введення дробів I. Отже, розглянемо множину (a,х а) б) ау = b х в) (це при умові, що b Відомо, що всяке відношення еквівалентності на множині визначає розбиття цієї множини на класи. Тому введене нами відношення рівності дробів в множині II. Доведемо, що множина
Ці означення коректні, бо кільце К є областю цілісності і тому із нерівностей xy
то Рівність (3) означає, що
Щоб довести рівності (4), треба довести рівності:
а для цього треба показати справедливість рівностей:
які в силу дистрибутивності і асоціативності рівносильні рівностям:
Якщо врахувати, що в кільці К множення комутативне, асоціативне і дистрибутивне, то перша з останніх рівностей одержується із вірних рівностей (5) домноженням першої з них на Таким чином, які б не брати дроби із класів Приступимо до перевірки виконання аксіом поля в множині
звідки внаслідок рівності правих частин одержуємо:
Щоб вказати нульовий елемент в множині
і з рівності Крім того, Отже, нулевим елементом в множині
Роль одиниці в множині К відіграє клас
Залишається тільки помітити, що множина
Таким чином, множина
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.2.160 (0.156 с.) |
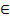 К рівняння а+х= b має єдиний розв’язок х= b +(-а), який називають різницею елементів b та а і позначають х= b -а.
К рівняння а+х= b має єдиний розв’язок х= b +(-а), який називають різницею елементів b та а і позначають х= b -а.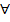 a, b
a, b 
 =
= 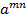 ,
,  =
= 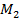 матриць 2-го порядку:
матриць 2-го порядку: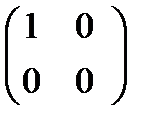
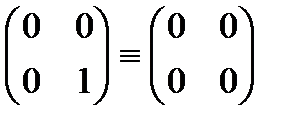 ,
, 
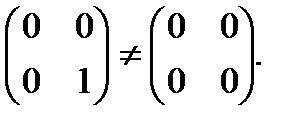
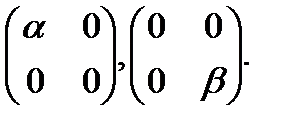 (α,β≠0).
(α,β≠0).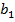 =а
=а 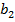 (
(  К) випливає:
К) випливає: 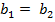 . Це означає, що рівності можна скорочувати на ненульовий елемент, який не є дільником нуля.
. Це означає, що рівності можна скорочувати на ненульовий елемент, який не є дільником нуля.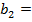 0
0 )=0.
)=0.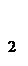 справедлива рівність
справедлива рівність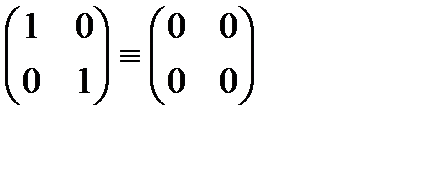
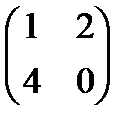
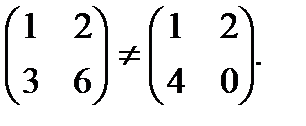
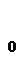 кільця К, яка сама є кільцем відносно операцій, означених в К, називається підкільцем кільця К.
кільця К, яка сама є кільцем відносно операцій, означених в К, називається підкільцем кільця К. кільця К є підкільцем кільця К тоді і тільки тоді, коли
кільця К є підкільцем кільця К тоді і тільки тоді, коли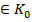 ): а+ b
): а+ b 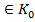 .
.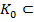 К є підкільцем К, то виконання умов 1)-3) гарантоване означенням кільця К.
К є підкільцем К, то виконання умов 1)-3) гарантоване означенням кільця К.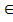 Р справедливо:
Р справедливо: усіх діагональних матриць n-го порядку є підкільцем кільця М
усіх діагональних матриць n-го порядку є підкільцем кільця М  усіх матриць n -го порядку над полем Р, бо сума, добуток діагональних матриць, і матриця, протилежна до діагональної, є діагональними.
усіх матриць n -го порядку над полем Р, бо сума, добуток діагональних матриць, і матриця, протилежна до діагональної, є діагональними.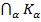 теж є підкільцем кільця К.
теж є підкільцем кільця К.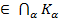 = Ко. Якщо а, b
= Ко. Якщо а, b 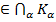 =
= 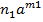 +
+ 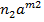 +….+
+….+ 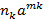 ,
,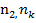 - довільні цілі числа,
- довільні цілі числа, 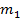 ,
, 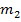 ,..
,.. 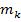 довільні натуральні числа, утворює підкільце кільця К, яке називається підкільцем, породженим елементом a. За означенням
довільні натуральні числа, утворює підкільце кільця К, яке називається підкільцем, породженим елементом a. За означенням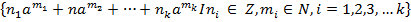
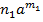 +
+  +….+
+….+ 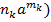 +(
+( 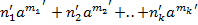 ) =(
) =( 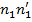 )
) 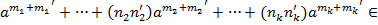 Кα
Кα 2.Гомоморфізми та ізоморфізми кілець
2.Гомоморфізми та ізоморфізми кілець що
що
 називається гомоморфізмом, якщо
називається гомоморфізмом, якщо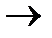
 =
= 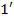 .
. ) (
) ( 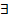 а
а 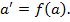
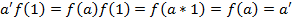
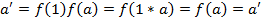
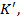 тобто f (1)=
тобто f (1)=  областю цілісності з одиницею
областю цілісності з одиницею 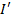 , то для всякого гомоморфізму f: K
, то для всякого гомоморфізму f: K 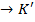 справедливо f (1) =
справедливо f (1) =  1)=f(a)f(1)
1)=f(a)f(1)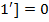
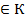 ): f (a)=0), то з наступної рівності виходить, що f (1)=
): f (a)=0), то з наступної рівності виходить, що f (1)=  Якщо існує обернений елемент для
Якщо існує обернений елемент для  для елемента а
для елемента а 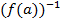 .
. )= f (1)=
)= f (1)=  }
}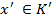 , для яких існують такі елементи х
, для яких існують такі елементи х 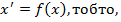
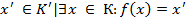 }.
}.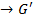 множини Ker f і Im f є підгрупами груп G і
множини Ker f і Im f є підгрупами груп G і 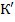 відповідно. До цього питання ми ще повернемось в параграфі 3.
відповідно. До цього питання ми ще повернемось в параграфі 3.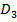 усіх діагональних матриць 3-го порядку.
усіх діагональних матриць 3-го порядку.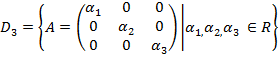
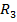 усіх трьохвимірних векторів
усіх трьохвимірних векторів
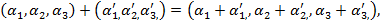
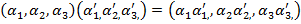

 таким способом: якщо
таким способом: якщо
 ,то
,то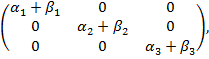 f (A)=
f (A)= 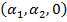 , f (B)=(
, f (B)=( )
)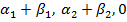 )=(
)=( = f (A)+ f (B);
= f (A)+ f (B);
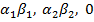 )=(
)=(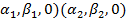 = f (A) f (B);
= f (A) f (B);
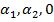 ) |
) | 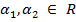 }
}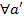 ,
, 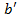 ,
,  М) (
М) (  = f(a),
= f(a), 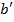 =f(b),
=f(b), 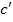 =f(c)
=f(c) (а)+
(а)+  +
+ 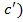 ;
; )
) 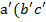 );
); +
+ 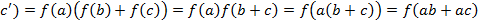 =f (ab)+f (ac)=f (a) f (b)+f (a) f (c)= а′ b′+ а′с′.
=f (ab)+f (ac)=f (a) f (b)+f (a) f (c)= а′ b′+ а′с′.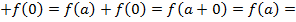 а′,
а′,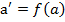 є елемент f (- a):
є елемент f (- a):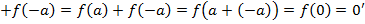 .
.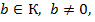 що ab = 0, то припустивши існування елемента
що ab = 0, то припустивши існування елемента 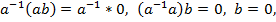 всупереч умові
всупереч умові 
 в якому всякий ненулевий елемент, що не є дільником нуля, має обернений. Обгрунтуємо зараз це твердження тільки для того випадку, коли К — область цілісності. Кільце K ′ виявиться при цьому полем. Отже, доведемо таку теорему.
в якому всякий ненулевий елемент, що не є дільником нуля, має обернений. Обгрунтуємо зараз це твердження тільки для того випадку, коли К — область цілісності. Кільце K ′ виявиться при цьому полем. Отже, доведемо таку теорему.
 , де m, n — цілі числа, тобто шляхом розгляду впорядкованих пар цілих чисел. Доведення теореми 2 зводиться до фактичної побудови поля
, де m, n — цілі числа, тобто шляхом розгляду впорядкованих пар цілих чисел. Доведення теореми 2 зводиться до фактичної побудови поля 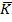 . Цю побудову здійснюватимемо аналогічно, як і при побудові поля раціональних чисел, тобто шляхом розгляду множини всіх впорядкованих пар елементів з кільця К.
. Цю побудову здійснюватимемо аналогічно, як і при побудові поля раціональних чисел, тобто шляхом розгляду множини всіх впорядкованих пар елементів з кільця К.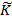 всіх впорядкованих пар (
всіх впорядкованих пар (
 ) елементів із кільця К. Ці пари зручно записувати у вигляді
) елементів із кільця К. Ці пари зручно записувати у вигляді  і називати дробами. Введемо в цій множині відношення рівності таким способом: дроби
і називати дробами. Введемо в цій множині відношення рівності таким способом: дроби 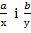 будемо називати рівними,
будемо називати рівними,  , якщо a у= b х. Так введемо відношення, яке є відношенням еквівалентності на множині
, якщо a у= b х. Так введемо відношення, яке є відношенням еквівалентності на множині  . Справді, відношення рівності задовольняє всім трьом умовам з означення відношення еквівалентності:
. Справді, відношення рівності задовольняє всім трьом умовам з означення відношення еквівалентності: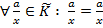 , бо a х= ах / рефлективність ̸;
, бо a х= ах / рефлективність ̸;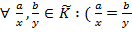 )
)  ), бо з рівності
), бо з рівності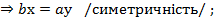
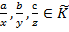 :(
:( бо перемноживши рівності ау= b х і bz = су (1). Одержимо (ау)(bz)=(b х)(су), звідси скориставшись асоціативністю і комутативністю множення в кільці К та властивістю
бо перемноживши рівності ау= b х і bz = су (1). Одержимо (ау)(bz)=(b х)(су), звідси скориставшись асоціативністю і комутативністю множення в кільці К та властивістю  а z = cx (2).
а z = cx (2). b =с, то в силу того, що в К немає дільників нуля, з рівності (1) випливатиме: а =0, с =0 і тоді рівність (2) очевидна).
b =с, то в силу того, що в К немає дільників нуля, з рівності (1) випливатиме: а =0, с =0 і тоді рівність (2) очевидна). визначає розбиття цієї множини класи рівних між собою дробів. Кожен такий клас є сукупністю всіх рівних між собою дробів і тому він повністю означається будь-яким своїм елементом
визначає розбиття цієї множини класи рівних між собою дробів. Кожен такий клас є сукупністю всіх рівних між собою дробів і тому він повністю означається будь-яким своїм елементом 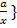 . Різні такі класи не містять рівних між собою дробів і об’єднання всіх таких класів співпадає із множиною
. Різні такі класи не містять рівних між собою дробів і об’єднання всіх таких класів співпадає із множиною 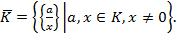
 операції додавання і множення. Введемо їх так:
операції додавання і множення. Введемо їх так: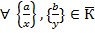 :{
:{ 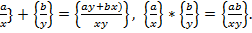
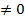 . Покажемо, що так введені операції є однозначними, тобто, що сума і добуток класів
. Покажемо, що так введені операції є однозначними, тобто, що сума і добуток класів  і
і 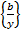 не залежить від вибору представників класів. Інакше кажучи, що коли
не залежить від вибору представників класів. Інакше кажучи, що коли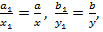 (3)
(3) (4)
(4)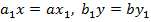 (5)
(5)

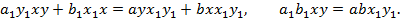
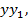 другої — на
другої — на 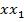 і наступним додаванням одержаних рівностей, а друга — почленним перемноження рівностей (5). Цим справедливість рівностей (4) доведена.
і наступним додаванням одержаних рівностей, а друга — почленним перемноження рівностей (5). Цим справедливість рівностей (4) доведена.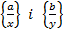 сума і добуток цих класів залишаються незмінними.
сума і добуток цих класів залишаються незмінними.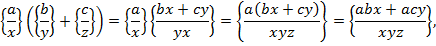

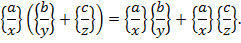
 утворює клас рівних дробів, бо
утворює клас рівних дробів, бо
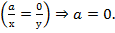
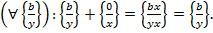
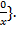 Протилежним елементом класу
Протилежним елементом класу 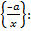
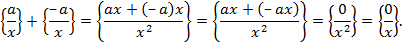
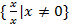 , який складається із усіх дробів з однаковими ненулевими чисельниками і знаменниками. Справді,
, який складається із усіх дробів з однаковими ненулевими чисельниками і знаменниками. Справді,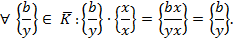
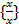 всіх дробів з рівними чисельниками і знаменниками справді утворює клас рівних дробів. Цей факт є наслідком того, що завжди
всіх дробів з рівними чисельниками і знаменниками справді утворює клас рівних дробів. Цей факт є наслідком того, що завжди 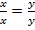 і завжди з рівності
і завжди з рівності 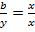 випливає bx = xy, тобто, b = y. Якщо клас
випливає bx = xy, тобто, b = y. Якщо клас 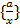 є ненулевим, тобто, a
є ненулевим, тобто, a 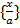 , що містить дріб
, що містить дріб 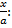
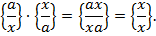
 і тому вона є полем.
і тому вона є полем.


