
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування конгруенцій до встановлення ознак подільності.
Як відомо, в кільці Z цілих чисел визначені операції додавання, віднімання і множення, а дія ділення не завжди можлива. Тому виникає потреба визначити, при яких умовах цілі числа діляться одно на одне. Подільність чисел – це певне відношення між числами, яке в Z + має такі властивості: рефлективність (a Між відношеннями подільності і Факт подільності двох чисел можна, звичайно, встановити за допомогою алгоритму ділення чисел з остачею. Проте для великих чисел це завдання досить складне. Тому бажано знайти зручні ознаки, за якими можна було б судити про подільність чисел, не виконуючи самого ділення. В цілому суть ознак подільності зводиться до того, що розгляд подільності деякого натурального числа a на натуральне число m змінюється розглядом подільності на число m іншого, меншого за a натурального числа b, яке можна знайти за деяким правилом, що визначається числовою функцією Одним із способів знаходження ознак подільності, основаних на конгруентності чисел, є так званий спосіб Паскаля1. Нехай деяке натуральне число
де коефіцієнти
На основі властивості 9 п. 15.1 Якщо число
Якщо ж b на число m не ділиться, то не ділиться на m і число a. За допомогою цієї загальної ознаки можна встановити зручні конкретні ознаки подільності чисел, записаних у звичайній для нас десятковій системі числення. У цій системі
Коротко це можна записати так: а) Ознака подільності на 2 і на 5. Оскільки Число a ділиться на 2 і на 5 тоді і тільки тоді, коли на них ділиться цифра одиниць числа a. Приклад 1. Число б) Ознака подільності на 3 і на 9. Оскільки всі остачі Отже, маємо таку ознаку: Число a ділиться на 3 (або на 9) тоді і тільки тоді, коли сума цифр, які його зображують, ділиться на 3 (або відповідно на 9). Приклад 2. Число в) Ознака подільності на 11. За модулем 11 маємо
Тому
Враховуючи, що цифри Число a ділиться на 11 тоді і тільки тоді, коли різниця між сумою цифр, які стоять на непарних місцях, і сумою цифр. Які стоять на парних місцях, ділиться на 11. Приклад 3. Число
ділиться на 11. У системі числення з основою
Порівнюючи це з (3), бачимо, що Враховуючи, що Число Ознаки подільності є цінними, якщо вони прості, зручні для користування. Проте більшість ознак, які можна вивести з ознаки Паскаля, є складними. Існує ряд зручних ознак подільності, які не випливають з загальної ознаки Паскаля, а знайдені іншими способами. Наприклад, одну з ознак подільності на 7 можна сформулювати так:
Число Зазначимо, що на відміну від усіх попередніх ознак числа Приклад 4. Оскільки Приклад 5. Встановити, чи ділиться на 7 число Приклад можна розв’язати так. Перш за все
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.60 (0.012 с.) |
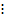 a), транзитивність (
a), транзитивність (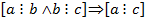 ) і антисиметричність
) і антисиметричність  . Будь-яке відношення, яке має властивості рефлективності, транзитивності і анти симетричності. Називається відношенням не строгого порядку. Отже, подільність чисел в Z + є відношенням не строгого порядку. Аналогічним відношенням частинної упорядкованості є, наприклад, відношення «
. Будь-яке відношення, яке має властивості рефлективності, транзитивності і анти симетричності. Називається відношенням не строгого порядку. Отже, подільність чисел в Z + є відношенням не строгого порядку. Аналогічним відношенням частинної упорядкованості є, наприклад, відношення « » в кільці Z. Воно рефлексивне
» в кільці Z. Воно рефлексивне  , транзитивне [ a
, транзитивне [ a 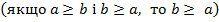 .
.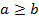 , або
, або 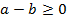 , означає, що існує таке число
, означає, що існує таке число 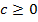 , при якому
, при якому 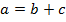 . Рівності
. Рівності 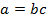 і
і 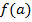 , тобто
, тобто  . При цьому числа
. При цьому числа  є, як кажуть. Рівноподільними на число
є, як кажуть. Рівноподільними на число 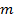 , тобто такі, які одночасно діляться або одночасно не діляться на число
, тобто такі, які одночасно діляться або одночасно не діляться на число 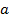 при основі числення
при основі числення 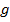 має вигляд
має вигляд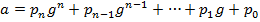 ,
,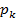 є натуральні числа, які задовольняють нерівності
є натуральні числа, які задовольняють нерівності 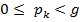 . Позначимо через
. Позначимо через 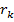 остачу від ділення числа
остачу від ділення числа 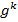 на
на 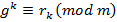 ,і побудуємо число
,і побудуємо число  за таким правилом:
за таким правилом: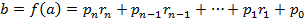
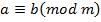 . Оскільки
. Оскільки 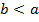 , то дістаємо таку ознаку Паскаля подільності чисел:
, то дістаємо таку ознаку Паскаля подільності чисел: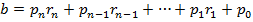 ділиться на число m, то ділиться на нього і число
ділиться на число m, то ділиться на нього і число 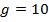 і число
і число 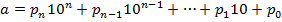
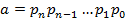 .
.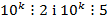 , то всі остачі
, то всі остачі 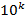 на числа 2 і 5 дорівнюють нулю. Тому за формулою (2) число
на числа 2 і 5 дорівнюють нулю. Тому за формулою (2) число 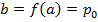 . Отже, маємо таку ознаку:
. Отже, маємо таку ознаку: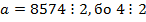 . Число 8127 не ділиться на 5, бо 7 не ділиться на 5.
. Число 8127 не ділиться на 5, бо 7 не ділиться на 5.
 .
.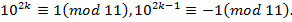
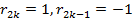 , і, отже, за рівністю (2)
, і, отже, за рівністю (2)
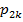 з парними індексами в числі
з парними індексами в числі 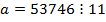 , бо число
, бо число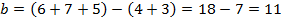
 можна знайти зручні ознаки подільності на числа 4, 25, 50. Число
можна знайти зручні ознаки подільності на числа 4, 25, 50. Число 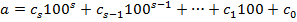
 , тобто є двоцифровим числом, яке зображується двома останніми цифрами числа
, тобто є двоцифровим числом, яке зображується двома останніми цифрами числа  і числа
і числа  діляться на числа 4, 25, 50, дістаємо такі ознаки подільності:
діляться на числа 4, 25, 50, дістаємо такі ознаки подільності: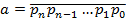 ділиться на 4 (або відповідно 25 чи 50) ділиться двоцифрове число
ділиться на 4 (або відповідно 25 чи 50) ділиться двоцифрове число 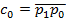 , утворене двома останніми цифрами числа
, утворене двома останніми цифрами числа 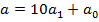 ділиться на 7 тоді і тільки тобі, коли ділиться на 7 число
ділиться на 7 тоді і тільки тобі, коли ділиться на 7 число  .
.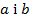 тут рівноподільні на7, а не конгруентні між собою за модулем
тут рівноподільні на7, а не конгруентні між собою за модулем 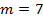 .
. .
.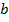 не ділиться на 7, то не ділиться на 7 і число 285. Зазначимо, що при діленні на 7 числа 285 дістаємо остачу 5, а при діленні на 7 числа 18 остача дорівнює 4 і тому
не ділиться на 7, то не ділиться на 7 і число 285. Зазначимо, що при діленні на 7 числа 285 дістаємо остачу 5, а при діленні на 7 числа 18 остача дорівнює 4 і тому  .
. .
. і тому
і тому  . А
. А 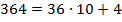 . Тому
. Тому  . Оскільки
. Оскільки 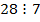 то й число
то й число  .
.


