
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Iv . Деякі інші означення групи
В літературі даються часто означення групи відмінні від означення 3 (див.приклад [1],[2]). Зараз ми ознайомимося з цими означеннями та доведемо їх еквівалентність означенню 3, тобто, покажемо, що всяка множина, яка задовольняє умови означення 3, задовольняє і умови означення 3’ та 3’’ і навпаки. Означення 3′. Не порожня множина G називається групою, якщо на ній означена одна алгебраїчна операція, яка задовольняє таким умовам: 1) алгебраїчна операція асоціативна; 2) В G існує ліва одиниця el , така, що 3) Для кожного елемента Означення 3 ′′. Непорожня множина G називається групою, якщо на ній означена одна алгебраїчна операція, яка задовольняє таким умовам: 1) Алгебраїчна операція асоціативна 2) Для всяких a, b ϵ G рівняння ax = b та ya = b мають розв’язки. Теорема 2. Означення 3 і 3′ еквівалентні. Доведення. Якщо множина є групою за означенням 3, тобто задовольняє умови означення 3, то вона задовольняє умови означення 3′, тобто є групою за означенням 3′. Одиничний елемент відіграє при цьому роль лівої одиниці, а обернений відіграє роль лівого оберненого. Нехай, навпаки, задовольняє умовам означення 3′. Щоб довести, що вона задовольняє умовам означення 3), досить, очевидно, показати, що ліва одиниця є одночасно і правою, тобто для і лівий обернений Покажемо спочатку справедливість співвідношення (4). Для цього домножимо рівність (2) справа на елемент ( В силу умови 3) означення 3′елемент
Оскільки a ′′- лівий обернений елемент до a e l(aa ′)= el або, інакше, aa ′ = el чим справедливість співвідношення (4) доведено. Переконаємось зараз в справедливості відношення (3). Для цього перетворимо ліву частину, використавши послідовно формулу (2), асоціативність множення, формули (4) і (1): ael = a (a / a)= (aa /) a = ela = a. Отже, множина G є групою і за означенням 3. Теорема 3. Означення 3 і Доведення. Якщо множина G задовольняє умови означення 3, то, як це безпосередньо випливає з означення 3 і властивості Навпаки, нехай множина G задовольняє умови означення Щоб довести існування в G лівої одиниці, тобто такого елемента
Отже, для ( Таким чином, множина G є групою згідно з означення Вправи. 1. Чи еквівалентні означення 2. Якщо множина G і підгрупою відносно до означення
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.0.240 (0.01 с.) |
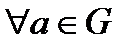 : ela = a (1)
: ela = a (1)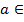 G відносно лівої одиниці el існує лівий обернений елемент
G відносно лівої одиниці el існує лівий обернений елемент 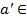 G, такий, що
G, такий, що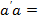 el .. (2)
el .. (2)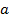 ’ є одночасно і правим оберненим, тобто
’ є одночасно і правим оберненим, тобто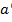 . Внаслідок однозначності операції множення (добуток двох елементів єдиний) рівність при цьому не порушується:
. Внаслідок однозначності операції множення (добуток двох елементів єдиний) рівність при цьому не порушується:
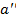 . Домноживши останню рівність зліва на елемент
. Домноживши останню рівність зліва на елемент 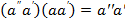
 , тобто a ′′ a ′ = el ,, то остання рівність перепишеться так:
, тобто a ′′ a ′ = el ,, то остання рівність перепишеться так: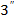 еквівалентні.
еквівалентні.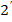 , вона задовольняє і умови означення
, вона задовольняє і умови означення 
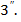 Ми покажемо, що множина при цьому задовольняє умови означення
Ми покажемо, що множина при цьому задовольняє умови означення 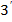 , звідки на підставі теореми 2 буде виходити, що множина G задовольняє і умови означення 3. Отже, треба показати, що в G існує ліва одиниця, по відношенні до якої кожен елемент має лівий обернений елемент.
, звідки на підставі теореми 2 буде виходити, що множина G задовольняє і умови означення 3. Отже, треба показати, що в G існує ліва одиниця, по відношенні до якої кожен елемент має лівий обернений елемент. , який задовольняє співвідношення (1), зауважимо, що за умовою рівняння у
, який задовольняє співвідношення (1), зауважимо, що за умовою рівняння у 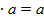 має розв’язок який позначимо через
має розв’язок який позначимо через  . покажемо, що
. покажемо, що  є лівою одиницею, тобто, що для (
є лівою одиницею, тобто, що для (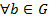 ):
): 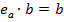 . З цією метою приймемо до уваги, що рівняння ax = b має розв’язок
. З цією метою приймемо до уваги, що рівняння ax = b має розв’язок 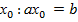 , внаслідок чого
, внаслідок чого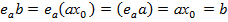
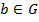 рівняння yb =
рівняння yb =  і
і 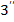 ?
?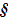 2. Підгрупи. Циклічні групи.
2. Підгрупи. Циклічні групи.


