
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определённого интеграла⇐ ПредыдущаяСтр 12 из 12
1) 2) 3) 4) 5) Если функция f (x) интегрируема на отрезках [ a; c ] и [ c; b ], то она интегрируема и на отрезке [ a; b ], причём верно равенство:
при любом расположении точек a, b и c на оси Ox. 6) Если f (x) ³ 0 при x Î [ a; b ], то
7) Если на отрезке [ a; b ] f (x) ³ g (x), то
8) Теорема 2 (о среднем значении определённого интеграла). Если функция f (x) непрерывна на отрезке [ a; b ], то на этом отрезке найдётся хотя бы одна точка c, в которой выполняется равенство:
Доказательство. Так как функция f (x) на отрезке [ a; b ] непрерывна, то она достигает на этом отрезке своих наименьшего “ m ” и наибольшего “ M ” значений. Тогда m £ f (x) £ M для любого x Î[ a; b ]. По свойству 7 определённого интеграла можно записать неравенство:
Так как m и M – постоянные числа, то
Вычислим по определению определённого интеграла
Тогда неравенство (*) можно переписать в виде:
Разделим все части полученного неравенства на (b – a) > 0 (длина отрезка интегрирования):
Так как функция f (x) непрерывна на отрезке [ a; b ], то она принимает все значения, заключённые между наименьшим “ m ” и наибольшим “ M ” значениями. Значит найдётся на отрезке [ a; b ] хотя бы одна точка c, в которой выполняется равенство:
Теорема доказана. Вычисление определенного интеграла. Формула Ньютона–Лейбница Интеграл с переменным верхним и постоянным нижним пределами и его свойства Определение 4. Пусть функция y = f (x) непрерывна на отрезке [ a; b ]. Тогда она непрерывна на отрезке [ a; x ] для любого x Î [ a; b ]. Следовательно, на отрезке [ a; b ] определена функция Свойства этой функции сформулируем в виде теоремы. Теорема 3. Пусть функция f (x) непрерывна на отрезке [ a; b ]. Тогда функция 1) непрерывна на отрезке [ a; b ]; 2) имеет производную F ' (x) в каждой точке x Î[ a; b ], удовлетворяющую равенству Доказательство. Вычислим приращение функции F (x), причём D x возьмём таким, чтобы точка x + D x Î [ a; b ]. Тогда
Применим к полученному интегралу теорему о среднем значении определённого интеграла, т.е. на отрезке [ x; x + D x ] существует такое число c, в котором выполняется равенство:
Значит, D F = f (c)×D x, где c Î [ x; x + D x ]. Если D x ® 0, то c ® x (так как x < c < x + D x). Поэтому, в силу непрерывности f (x), получим f (c) ® f (x) при D x ®0. Таким образом, D F ®0 при D x ®0, что доказывает непрерывность F (x). Кроме того, вычисляя предел отношения D F к D x при D x ® 0, получим:
т.е. существует конечный предел отношения D F к D x при D x ® 0, что означает существование производной F ' (x) = f (x). Теорема доказана. Из теоремы 3 следует, что функция
Формула Ньютона–Лейбница Теорема 4. Пусть функция f (x) непрерывна на отрезке [ a; b ] и F(x) – какая-либо её первообразная на отрезке [ a; b ]. Тогда определённый интеграл от функции f (x) по отрезку [ a; b ] равен разности значений функции F(x) в точках b и a:
Доказательство. Из теоремы 3 следует, что наряду с функцией F(x) функция Вычислим значение const. Для этого, используя свойство 1 определённого интеграла (§3, п.2, с. 93)
Следовательно, равенство (**) можно переписать в виде:
Теперь рассмотрим полученное равенство при x = b:
Это и есть формула Ньютона–Лейбница. Она является основной формулой интегрального исчисления, устанавливающей связь между определённым и неопределённым интегралами, и даёт правило вычисления определённого интеграла. Замечание. Формулу Ньютона–Лейбница часто записывают в виде:
где используется обозначение:
Задача вычисления определённого интеграла свелась к нахождению первообразной непрерывной функции. Пример 1. Вычислить интеграл:
Ответ: Пример 2. Вычислить интеграл:
Ответ:
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.014 с.) |
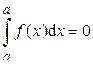
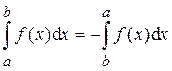
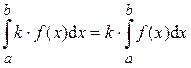
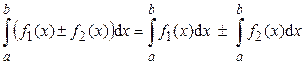
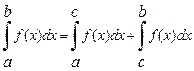
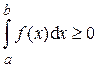
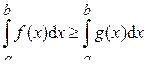
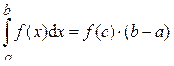
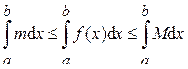
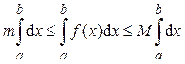 (*)
(*)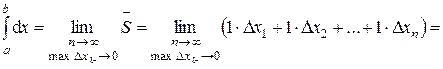
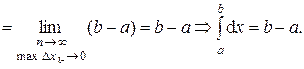
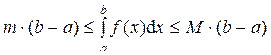 .
.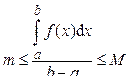
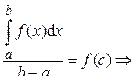
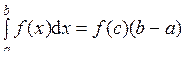 .
.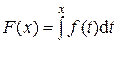 , которая называется интегралом с переменным верхним пределом.
, которая называется интегралом с переменным верхним пределом.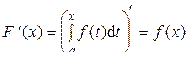 .
.
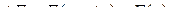
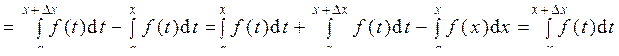 .
.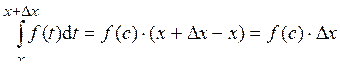
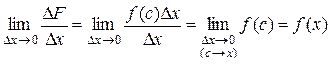 ,
,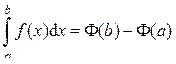
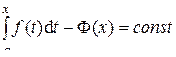 для любого x Î [ a; b ] (**)
для любого x Î [ a; b ] (**)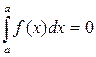 , рассмотрим равенство (**) при x = a:
, рассмотрим равенство (**) при x = a: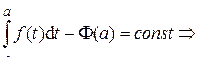
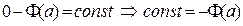
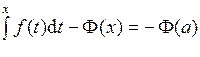 для x Î [ a; b ]
для x Î [ a; b ]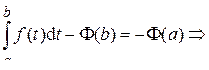
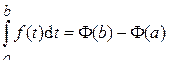
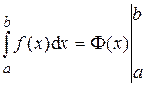 ,
,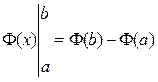 .
.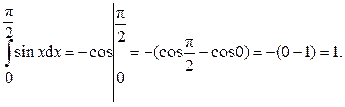
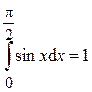 .
.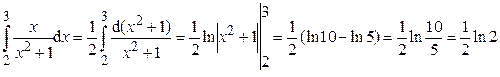 .
.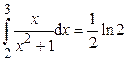 .
.


