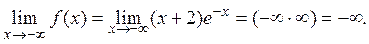Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема исследования функции. Построение графика
1) Найти область определения функции y = f (x) – множество D (f) тех значений x, при которых функция y = f (x) имеет смысл. 2) Исследовать функцию на периодичность: выяснить, существует ли наименьшее положительное число T такое, что f (x + T) = f (x) для любого x Î D (f). Если «да», то целесообразно далее исследовать функцию и строить её график только на некотором отрезке длиной периода T. Затем продолжить график на всю область определения, разбивая её на интервалы длины T, в которых повторяется картинка графика. 3) Исследовать функцию на чётность и нечётность: выяснить, выполняются ли равенства: f (– x) = f (x) для любого x Î D (f) – чётность или f (– x) = – f (x) для любого x Î D (f) – нечётность. Это позволяет узнать, есть ли симметрия графика: относительно оси O y – чётная или относительно начала координат – нечётная. 4) Найти точки пересечения графика функции · с осью O y: точка (0; f (0)), если 0 Î D (f), · с осью O х: точка (x k; 0), где x kÎ D (f) и является решением уравнения f (x) = 0. 5) Найти промежутки знакопостоянства: выяснить, при каких x Î D (f) выполняются неравенства f (x) > 0 (график функции расположен выше оси O x) и f (x) < 0 (график функции расположен ниже оси O x). 6) Исследовать функцию на непрерывность, установить тип точек разрыва (см. §3, п.2, с. 19). 7) Найти вертикальные и наклонные асимптоты (см. §6, п.1, с. 43). 8) Найти промежутки убывания и возрастания, экстремумы функции (см. §6, п.2, с. 45 и п.3, с. 46). 9) Найти множество E (f) значений функции. 10) Найти промежутки выпуклости, вогнутости и точки перегиба графика (см. §6, п.4, с. 49). 11) Построить график функции, используя свойства, установленные в проведенном исследовании. Если в некоторых промежутках график остался неясным, то его уточняют по дополнительным точкам. Пример. Исследовать функцию y = (x + 2) e – x и построить её график. 1) D (y) = R. 2) Функция не периодическая. 3) Так как y (– x) ≠ y (x) и y (– x) ≠ – y (x), то функция общего вида, не является ни чётной, ни нечётной. 4) Точка пересечения графика с осью O x: (– 2; 0), с O y: (0; 2) 5) При x Î (–¥; –2) функция отрицательная, при x Î (–2; +¥) функция положительная. 6) Функция непрерывна при x Î R. 7) Вертикальных асимптот нет. Наклонные асимптоты: y = kx + b. а)
b = 0 при
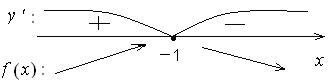
Следовательно, y = 0 – наклонная (горизонтальная) асимптота при б) при 8) f '(x) = ((x + 2) e – x ) ' = 1× e – x +(x + 2)×(– e – x ) = e – x (1 – x – 2) = –(x + 1) e – x . D (y ') = R. y ' = 0: – (x +1) e – x = 0 Þ x = – 1, f (–1) = 1× e 1 = e.
при x Î (– ¥;– 1) f (x) возрастает, при x Î(– 1;+¥) f (x) убывает, при x = –1 f max (– 1) = (– 1+2) e – (– 1) = e. 9) E (f) = (–¥; e), так как
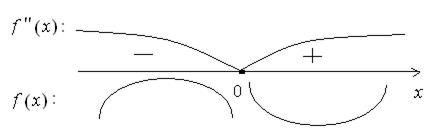
и f max (–1) = e. 10) f ''(x) = (– (x + 1) e – x) ' = – 1 e – x + (x + 1) e – x = e – x (x + 1 – 1) = xe – x. D (f '') = R f '' (x) = 0: xe – x = 0 Þ x = 0, f (0) = 2.
при x Î (– ¥;0) график f (x) выпуклый при x Î (0;+¥) график f (x) вогнутый Точка (0;2) – точка перегиба графика. 11) Результаты проведенного исследования cведём в таблицу и построим график (рис. 12) Таблица Результаты исследования функции y = (x + 2) e – x
Рис. 12
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.148 (0.028 с.) |
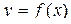 с осями координат:
с осями координат:
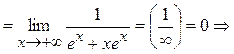 k = 0 при x ® +¥
k = 0 при x ® +¥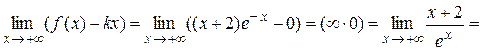


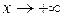 .
.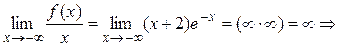
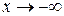 наклонной асимптоты нет.
наклонной асимптоты нет.