
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И интегральное исчисление функцииСтр 1 из 12Следующая ⇒
Дифференциальное И интегральное исчисление функции Одной переменной
Утверждено Редакционным советом университета в качестве учебного пособия
Москва 2012 УДК 517 (075) ББК 22.161.1 Д50
Авторы: Е. Г. Рудаковская, М. Ф. Рушайло, М. А. Меладзе, Е. Л. Гордеева, В. В. Осипчик
Рецензенты: Доктор технических наук, профессор Российского химико-технологического университета им. Д. И. Менделеева Л. С. Гордеев Кандидат физико-математических наук, доцент Московского автомобильно-дорожного государственного технического университета (МАДИ) С. А. Изотова
Дифференциальное и интегральное исчисление функции одной Д50 переменной: учеб. пособие / Е. Г. Рудаковская, М. Ф. Рушайло, М. А. Меладзе, Е. Л. Гордеева, В. В. Осипчик; под ред. Е. Г. Рудаковской, М. Ф. Рушайло. М.: РХТУ им. Д. И. Менделеева, 2012. – 108 с. ISBN 978-5-7237-0993-5
Пособие представляет сжатое изложение лекций по математическому анализу, читаемых кафедрой высшей математики. Пособие охватывает следующие разделы курса математического анализа: дифференциальное исчисление функций одной переменной, интегральное исчисление функций одной переменной. Большое внимание уделено разбору примеров по изучаемым темам, имеющим прикладное значение для других дисциплин. Предназначено для студентов I курса всех факультетов и колледжей РХТУ им. Д. И. Менделеева.
УДК 517 (075) ББК 22.161.1
ISBN 978-5-7237-0993-5 © Российский химико-технологический университет им. Д. И. Менделеева, 2012 Оглавление
ГЛАВА 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.. 3 § 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ, ОСНОВНЫЕ ПОНЯТИЯ.. 3 1. Определение функции одной переменной. 3 2. Способы задания функции. 3 3. Сложная и обратная функции. 3 4. Элементарные функции. 3 § 2. ПРЕДЕЛ ФУНКЦИИ.. 3 1. Предел функции в конечной точке x 0 3 2. Односторонние пределы.. 3 3. Предел функции на бесконечности. 3 4. Бесконечно малые и бесконечно большие функции. 3 5. Основные теоремы о конечных пределах. 3 6. Первый замечательный предел. 3 7. Второй замечательный предел. 3 § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ.. 3 1. Непрерывность функции в точке и на промежутке. 3
2. Точки разрыва функции и их классификация. 3 § 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.. 3 1. Определение производной, её геометрический и механический смысл. …….3 2. Примеры вывода производных некоторых элементарных функций. 3 3. Таблица производных основных элементарных функций. 3 4. Дифференцируемость функции. Связь дифференцируемости с существованием производной и непрерывностью функции. 3 5. Правила дифференцирования. 3 6. Дифференцирование функции, заданной неявно. 3 7. Производные показательной и степенной функций. 3 8. Производные обратных тригонометрических функций. 3 9. Дифференциал функции. 3 10. Производные и дифференциалы высших порядков. 3 § 5. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ……...37 1. Теорема Ролля. 3 2. Теорема Лагранжа. 3 3. Теорема Коши. 3 4. Правило Лопиталя. 3 § 6. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ.. 3 1. Асимптоты плоской кривой. 3 2. Монотонность функции. 3 3. Экстремумы функции. 3 4. Выпуклость, вогнутость и точки перегиба графика функции. 3 5. Наибольшее и наименьшее значения функции на отрезке. 3 6. Схема исследования функции. Построение графика. 3 ГЛАВА 2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 3 § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.. 3 1. Первообразная функция и её свойства. 3 2. Понятие неопределённого интеграла. 3 3. Свойства неопределённого интеграла. 3 4. Таблица основных неопределённых интегралов. 3 § 2. МЕТОДЫ ИНТЕГРИРОВАНИЯ.. 3 1. Непосредственное интегрирование. 3 2. Интегрирование подстановкой. 3 3. Интегрирование по частям. 3 4. Интегрирование рациональных дробей. 3 5. Интегрирование тригонометрических выражений. 3 6. Интегрирование некоторых видов иррациональных выражений. 3 § 3. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.. 3 1. Задача, приводящая к определённому интегралу. 3 2. Свойства определённого интеграла. 3 3. Вычисление определенного интеграла. Формула Ньютона–Лейбница. …....3 4. Методы интегрирования определённого интеграла. 3 5. Приложения определённого интеграла. 3 § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ.. 3 1. Интегралы с бесконечными пределами. 3 2. Интегралы от разрывных функций. 3
ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ, ОСНОВНЫЕ ПОНЯТИЯ Сложная и обратная функции Определение 1. Пусть функция y = f (U) определена на множестве D (f), а функция U = g (x) определена на D (g), причём E (g) Тогда функция y = F (x) = f (g (x)) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g). Определение 2. Пусть задана функция y = f (x) взаимно однозначно отображающая множество X = D (f) на множество Y = E (f). Тогда функция x = g (y) называется обратной к функции y = f (x), т. е. любому y Замечание. Графики функций y = f (x) и x = g (y) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x, а зависимую y, то графики функций y = f (x) и y = g (x) будут симметричны относительно биссектрисы первого и третьего координатных углов.
Элементарные функции Основные элементарные функции: y = const (постоянная функция), D (y) = R; E (y) = c.
y = y = y = Тригонометрические функции: y = sin x, D (y) = R, E (y) = y = cos x, D (y) = R, E (y) = y = tg x, D (y) = y = ctg x, D (y) = Обратные тригонометрические функции: y = arcsin x, D (y) = y = arccos x, D (y) = y = arctg x, D (y) = R, E (y) = y = arcctg x, D (y) = R, E (y) = Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции. Например:
Графики обратных тригонометрических функций:
ПРЕДЕЛ ФУНКЦИИ 1. Предел функции в конечной точке x0
Определение 2. d-Окрестностью точки x 0называется интервал (
Определение 3. Проколотой d-окрестностью точки x 0 называется d-окрестность точки x 0 без самой точки x 0:
Определение 4. Число А называется пределом функции f (x) при x ® x 0, если для любого малого числа ε > 0 существует такое малое число Итак: Односторонние пределы Определение 5. Число А называется правым (левым) пределом функции y = f (x) в точке x 0, если для любого малого числа ε > 0 найдётся другое малое число При этом используют следующие обозначения:
Замечание 1. Если f (x) имеет в точке x 0, предел равный А, то существуют
Замечание 2. Если f (x) имеет в точке x 0 правый
Замечание 3. Если f (x) имеет в точке x 0 правый Первый замечательный предел
Теорема 6. Предел функции Доказательство:
1) Пусть угол x > 0 (x
где угол х в радианах. Подставим в соотношение (1) полученные значения площадей:
Так как все части двойного неравенства положительные, выражение можно переписать так:
Так как
2) Пусть x < 0 (x
Теорема доказана.
Второй замечательный предел Теорема 7. Предел функции
Замечание. Число e является пределом последовательности
НЕПРЕРЫВНОСТЬ ФУНКЦИИ Примеры вывода производных некоторых элементарных функций 1) Вывод:
2) Вывод:
3) Вывод:
(используется второй замечательный предел и свойства логарифма).
4) Вывод: так как ln x = log e x, то, используя производную, для (log a x), можно записать:
5) (c)' = 0 Вывод: y = c, D y = y (x +D x) – y (x) = c – c = 0 Для остальных функций производные выводятся позже с помощью правил дифференцирования. Таблица производных основных элементарных функций 1. (c)' = 0 2. (x a)' = a× x a – 1 3. (ax)' = ax ×ln a, (a > 0, a ≠ 1) 4. (ex)' = ex 5. (lo ga x)' = 6. (ln x)' = 7. (sin x)' =cos x 8. (cos x)' = – sin x 9. (tg x)' = 10. (ctg x)' = – 11. (arcsin x)' = 12. (arccos x)' = – 13. (arctg x)' = 14. (arcctg x)' = Правила дифференцирования Теорема 3. Если функции U (x) и V (x) дифференцируемы в точке x, то функция U (x) ± V (x) дифференцируема в точке x и её производная вычисляется по формуле: (U (x) ± V (x))' = (U (x))' ± (V (x))'. Доказательство: Рассмотрим функцию y = U (x) ± V (x). Тогда D y = D U ± D V. Разделим на D x и перейдём к пределу при D x ® 0:
так как по условию теоремы функции U (x) и V (x) дифференцируемы. Значит, (U (x) ± V (x))' = U '(x) ± V '(x). Теорема доказана. Теорема 4. Если функции U (x) и V (x) дифференцируемы в точке х, то функция (U (x)× V (x)) дифференцируема в точке х и её производная вычисляется по формуле: (U (x) × V (x))' = (U (x))'× V (x) + U (x) × (V (x))'.
Доказательство. Рассмотрим функцию D y = (U +D U)(V +D V) – U × V = U × V + U ×D V + V ×D U + D U ×D V – U × V = = U ×D V + V ×D U + D U ×D V. Разделим D y на D x и перейдем к пределу при D x ® 0:
так как по условию функции U (x) и V (x) дифференцируемы, а значит Следовательно, (U (x)× V (x))' = U ' (x) × V (x) + U (x) × V ' (x). Теорема доказана. Следствия: а) Если U (x), V (x) и W (x) дифференцируемы в точке х, то функция (U (x)× V (x) × W (x)) дифференцируема в точке х и её производная вычисляется по формуле:
(U × V × W)' = U '× V × W + U × V '× W + U × V × W '. б) Производная постоянной, умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на производную функции:
(C× U (x))' = C× U ' (x). Теорема 5. Если функции U (x) и V (x) дифференцируемы в точке х и V (x) ≠ 0, то функция
Доказательство. Рассмотрим функцию Разделим D y на D x и перейдём к пределу при D x ® 0:
Значит,
Теорема доказана. Теорема 6 (производная сложной функции). Если функция f (u) дифференцируема в точке u, а функция u (x) дифференцируема в точке x, причём u = u (x), тогда сложная функция f (u (x)) дифференцируема в точке x и её производная вычисляется по формуле: (f (u (x)))' = f '(u) × u ' (x). Доказательство. Рассмотрим функцию y = f (u). Так как функция f (u) дифференцируема в точке u, то её приращение можно записать в виде:
где Разделим на D x и перейдём к пределу при D x ® 0:
Если D x ® 0, то D u ® 0, так как u (x) дифференцируема, а значит непрерывна, т.е. (f (u (x)))' = f ' (u) × u ' (x). Теорема доказана. Дифференциал функции Пусть функция y = f (x) дифференцируема в точке x, тогда её приращение можно записать в виде двух слагаемых, первое из которых линейно относительно D x, а второе слагаемое – бесконечно малая величина при D x ® 0 (более высокого порядка малости по сравнению с D x):
где Определение 4. Слагаемое
d y = y ' (x)× D x. Если x – независимая переменная, то справедливо равенство D x = d x, так как (x)' = 1. Тогда формула для дифференциала записывается:
d y = y ' (x)× d x. Так как второе слагаемое приращения функция – малая величина более высокого порядка малости по сравнению с D x, то между приращением функции и её дифференциалом можно приближённо поставить знак равенства. Это равенство тем точнее, чем меньше D x. На основе этого приближённого равенства получается приближённое представление значения дифференцируемой функции:
Пример. Вычислить приближённо Решение. Рассмотрим функцию возьмём x 0 = 4, приращение D x = 0,08,
где D << 0,08.
Теорема Ролля Теорема 4 (теорема Ролля). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия:
· f (x) непрерывна на отрезке [ a; b ]; · f (x) дифференцируема на интервале (a; b); · f (a) = f (b), то внутри этого отрезка [ a; b ] найдется хотя бы одна точка х 0, в которой выполняется равенство: f '(х 0) = 0. Доказательство. Так как f (x) непрерывна на отрезке [ a; b ], то она достигает на этом отрезке своих наименьшего m и наибольшего M значений. Возможны два случая: m = M и m < M. · Если m = M, то f (x) = const = m = M. Тогда f '(x) = 0 при любом x Î [ a; b ]. Следовательно, в этом случае теорема верна и при этом в качестве х 0 можно рассматривать любое значение x Î [ a; b ]. · Если m < M, то исходя из условия f (a) = f (b), по крайней мере одно из чисел m или M не равно f (a) = f (b). Для определённости предположим, что M – наибольшее значение f (x) достигается не на концах отрезка [ a; b ], а в некоторой внутренней точке х 0 Î (a; b). Тогда в точке х 0 для приращения функции справедливо неравенство: D y = f (х 0 + D x) – f (х о) ≤ 0, так как f (х 0) = M – наибольшее значение f (x) на отрезке [ a; b ] и D x такое, что х 0 + D x Î [ a; b ]. · Если D x > 0, то · Если D x < 0, то Так как по условию теоремы функция f (x) дифференцируема при x Î (a; b), то в точке х о существует производная. Значит справедливы равенства: f ' (х 0 + 0) = f ' (х 0 – 0) = f ' (х 0) = 0. Теорема доказана. Теорема Лагранжа Теорема 5 (теорема Лагранжа). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ], · f (x) дифференцируема на интервале (a; b), то внутри этого отрезка существует хотя бы одна точка х 0, в которой выполняется равенство: f ' (х 0) = Доказательство. Рассмотрим вспомогательную функцию F (x) = f (x) + l× x, где l = const. Потребуем, что бы для F (x) выполнялось условие F (a) = F (b). Так как F (a) = f (a) + l× a и F (b) = f (b) + l× b, то получим равенство: f (a) + l× a = f (b) + l× b. Отсюда выразим значение l: l = – При этом значении l функция F (x) = f (x) – Функция F (x) удовлетворяет всем условиям теоремы Ролля: · F (x) непрерывна на отрезке [ a; b ]: · F (x) дифференцируема на интервале (a; b) · F (a) = F (b). Следовательно, по теореме Ролля на интервале (a; b) существует хотя бы одна точка х 0, в которой выполняется равенство: F '(х 0) = 0. Найдём F '(x): F '(x) = f '(x) – Поэтому F '(x 0) = f '(х 0) – Теорема доказана. Теорема Коши Теорема 6 (теорема Коши). Если функции f (x) и g (x) определены на отрезке [ a; b ] и удовлетворяют условиям: · f (x) и g (x) непрерывны на отрезке [ a; b ]; · f (x) и g (x) дифференцируемы на интервале (a; b); · g '(x) ¹ 0 при любом x Î (a; b), то внутри отрезка [ a; b ] найдётся хотя бы одна точка х 0, в которой выполняется равенство:
Доказательство аналогично доказательству теоремы 5 (теорема Лагранжа) при вспомогательной функции F (x) = f (x) + l × g (x), где l = const, которую выбирают так, чтобы F (a) = F (b). Правило Лопиталя Теорема 7 (правило Лопиталя). Если функции f (x) и g (x) определены в некоторой окрестности точки х 0 и в этой окрестности они удовлетворяют условиям: · f (x) и g (x) дифференцируемы в каждой точке за исключением может быть самой точки х 0; · g '(x) ¹ 0 для любого x из этой окрестности; · тогда, если существует
Замечание 1. Правило Лопиталя используется для раскрытия неопределённостей типа Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость функций f '(x) и g '(x) в окрестности точки х 0, то при выполнении остальных требований для f '(x) и g '(x) правило Лопиталя можно применить повторно. При этом будет справедливо равенство:
Пример 1. Вычислить предел:
Пример 2. Вычислить предел:
Пример 3. Вычислить предел:
Пример 4. Вычислить предел:
Пример 5. Вычислить предел:
Пример 6. Вычислить предел:
Асимптоты плоской кривой Определение 1. Если точка M (x; y) перемещается по кривой y = f (x) так, что хотя бы одна из координат точки стремится к ¥ и при этом расстояние от этой точки до некоторой прямой стремится к 0, то эта прямая называется асимптотой кривой y = f (x). Асимптоты бывают двух видов: вертикальные и наклонные. Определение 2. Прямая x = a называется вертикальной асимптотой кривой y = f (x), если хотя бы один из односторонних пределов Замечание. Если прямая x = a является вертикальной асимптотой кривой y = f (x), то в точке x = a функция f (x) имеет разрыв второго рода. Наоборот, если в точке x = a функция f (x) имеет разрыв второго рода, то прямая x = a является вертикальной асимптотой кривой y = f (x). Определение 3. Прямая
где Теорема 1. Для того чтобы кривая y = f (x) имела наклонную асимптоту при
Доказательство. Ограничимся случаем Необходимость. Пусть y = kx + b – наклонная асимптота при
Убедимся в существовании конечных пределов:
Необходимость доказана. Достаточность. Пусть существуют конечные пределы Тогда по свойству конечных пределов второй предел можно переписать в виде:
где Отсюда получаем:
где Достаточность доказана. Пример 1. Найти асимптоты кривой Решение. 1) D (y) = (–¥;–1) È (–1;1) È (1;+ ¥). 2) Точки x = –1 и x = 1 являются точками разрыва второго рода, так как:
Поэтому прямые x = –1 и x = 1 являются вертикальными асимптотами. 3) Вычислим пределы:
Отсюда следует, что при Найдём наклонную асимптоту при Вычисляя те же пределы при Ответ: x = ± 1 – вертикальные асимптоты y = x – наклонная асимптота при x ® ±¥. Монотонность функции Определение 4. Функция y = f (x) называется возрастающей (убывающей) на промежутке (a; b), если для любых x 1 и x 2, принадлежащих этому промежутку, из условия x 2 > x 1 следует неравенство:
f (x 2) > f (x 1) (f (x 2) < f (x 1)).
Определение 5. Функция y = f (x) называется монотонной на промежутке (a; b), если она на этом промежутке является только возрастающей или только убывающей. Теорема 2 (достаточные условия монотонности). Если функция y = f (x) дифференцируема на промежутке (a; b) и f ’ (x) > 0 (f ’ (x) < 0) для любых x Î (a; b), то функция возрастает (убывает) на этом промежутке. Доказательство. Возьмём любые два значения x 1 и x 2 из промежутка (a; b). Для определённости предположим, что x 2 > x 1. На отрезке [ x 1; x 2] функция y = f (x) непрерывна и дифференцируема (из условия теоремы). Следовательно, она удовлетворяет теореме Лагранжа на отрезке [ x 1; x 2], т.е. существует хотя бы одна точка c Î (x 1; x 2), в которой выполняется равенство: f (x 2) – f (x 1) = f ' (c) × (x 2 – x 1). Если f '(x) > 0 для любых x Î(a; b), то f '(c) > 0. Поэтому f (x 2) – f (x 1) > 0, т.е. из условия x 2 > x 1 следует неравенство f (x 2) > f (x 1). А так как x 1 и x 2 –любые значения из промежутка (a; b), то функция y = f (x) возрастает на этом промежутке. Если Теорема доказана. Экстремумы функции
|
|||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.192.100 (0.284 с.) |
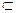 D (f).
D (f).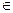 E (f) соответствует единственное значение x
E (f) соответствует единственное значение x 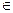 D (f), при котором верно равенство y = f (x).
D (f), при котором верно равенство y = f (x).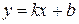 (линейная функция), D (y) = R; E (y) = R.
(линейная функция), D (y) = R; E (y) = R.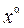 (степенная функция), α Î R, E (y), D (y) зависят от α.
(степенная функция), α Î R, E (y), D (y) зависят от α.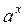 (показательная функция), a > 0, a ≠ 1, D (y) = R, E (y) = (0;+∞).
(показательная функция), a > 0, a ≠ 1, D (y) = R, E (y) = (0;+∞).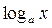 (логарифмическая функция)), a > 0, a ≠ 1, D (y) = (0;+∞), E (y) = R.
(логарифмическая функция)), a > 0, a ≠ 1, D (y) = (0;+∞), E (y) = R. .
.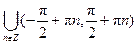 , E (y) = R.
, E (y) = R.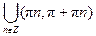 , E (y) = R.
, E (y) = R.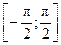 .
.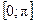 .
.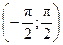 .
.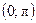 .
.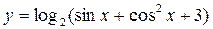 – элементарная функция.
– элементарная функция.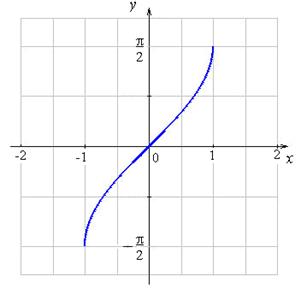 Рис. 1
Рис. 1
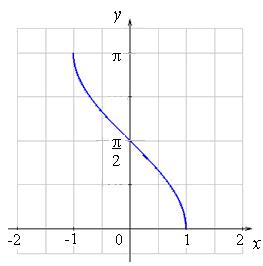 Рис. 2
Рис. 2
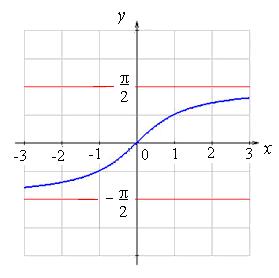 Рис. 3
Рис. 3
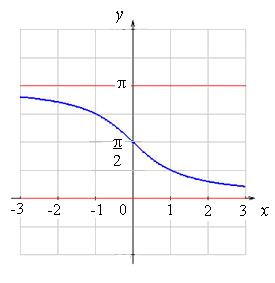 Рис. 4
Рис. 4
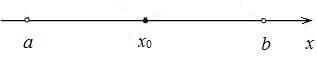
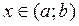 .
.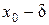 ;
; 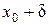 ), длина которого 2d, симметричный относительно x 0:
), длина которого 2d, симметричный относительно x 0: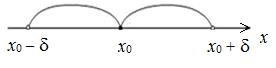
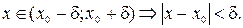
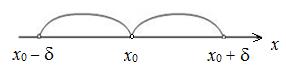
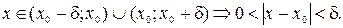
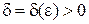 , что для любого x, принадлежащего D(f) и проколотой δ-окрестности точки x 0, т.е.
, что для любого x, принадлежащего D(f) и проколотой δ-окрестности точки x 0, т.е. 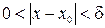 , выполняется неравенство:
, выполняется неравенство: 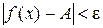 .
.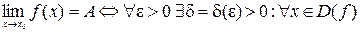 и
и 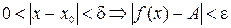 .
.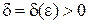 – такое, что для всех
– такое, что для всех 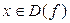 и лежащих в правой (левой) окрестности точки x 0, т.е.
и лежащих в правой (левой) окрестности точки x 0, т.е. 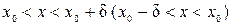 , справедливо неравенство:
, справедливо неравенство: 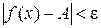 .
.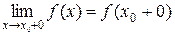 – для правого предела.
– для правого предела.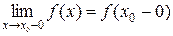 – для левого предела.
– для левого предела.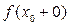 и
и 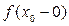 и справедливо равенство:
и справедливо равенство: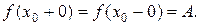 .
.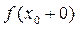 и левый
и левый 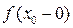 пределы, равные между собой, то в точке
пределы, равные между собой, то в точке 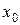 функция f (x) имеет предел, равный числу:
функция f (x) имеет предел, равный числу: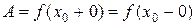 .
.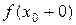 и левый
и левый 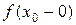 пределы, но они не равны между собой, то в точке x 0 функция f (x) не имеет предела.
пределы, но они не равны между собой, то в точке x 0 функция f (x) не имеет предела.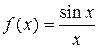 в точке
в точке 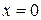 существует и равен 1, т.е.
существует и равен 1, т.е. 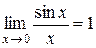 .
.
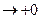 ). Площади
). Площади 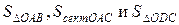 соотносятся:
соотносятся: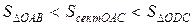 (1)
(1) ;
; 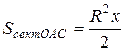 ;
; 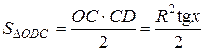 ,
,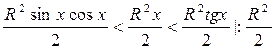 ,
,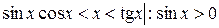 ,
,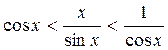
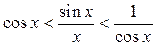
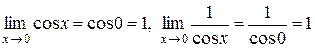 то по теореме 5:
то по теореме 5: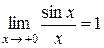 .
.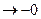 )
)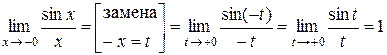 (по доказанному в первом случае). Следовательно,
(по доказанному в первом случае). Следовательно,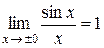 .
. при x
при x 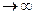 существует и равен числу e, т.е.
существует и равен числу e, т.е.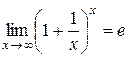 .
.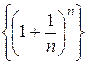 , причем это число иррациональное, т.е. представляется бесконечной непериодической десятичной дробью: e = 2,7182818284590…. Более того, число e трансцендентное, т.е. не является корнем алгебраического уравнения с целыми коэффициентами. В математическом анализе это число играет особую роль, в частности, является основанием натурального логарифма. Показательная функция с основанием e:
, причем это число иррациональное, т.е. представляется бесконечной непериодической десятичной дробью: e = 2,7182818284590…. Более того, число e трансцендентное, т.е. не является корнем алгебраического уравнения с целыми коэффициентами. В математическом анализе это число играет особую роль, в частности, является основанием натурального логарифма. Показательная функция с основанием e: 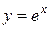 , называется экспонентой.
, называется экспонентой.
 ;
; 


 ;
; ;
; 



 ;
; 



 .
. .
. , (a > 0; a ≠ 1)
, (a > 0; a ≠ 1)






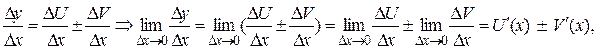
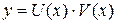 . Найдём её приращение
. Найдём её приращение
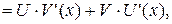
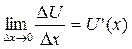 ,
, 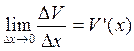 и
и 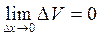 .
.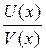 дифференцируема в точке х и её производная вычисляется по формуле:
дифференцируема в точке х и её производная вычисляется по формуле: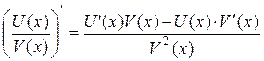 .
. . Найдём её приращение
. Найдём её приращение 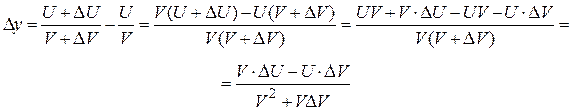
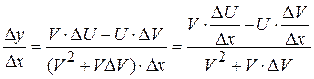 ,
,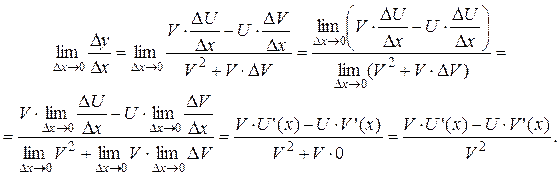
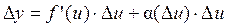 ,
,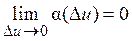 .
.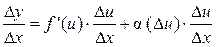
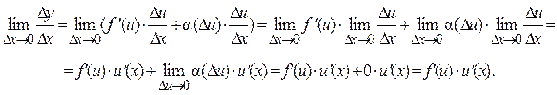
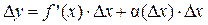 ,
,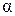 (D x) ® 0 при D x ® 0.
(D x) ® 0 при D x ® 0.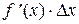 называется главной линейной относительно D x частью приращения функции y = f (x), называемой дифференциалом этой функции. Дифференциал обозначается
называется главной линейной относительно D x частью приращения функции y = f (x), называемой дифференциалом этой функции. Дифференциал обозначается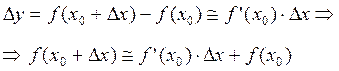
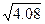
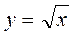 . В качестве начальной точки
. В качестве начальной точки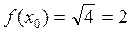 и подставим в формулу:
и подставим в формулу: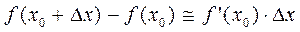
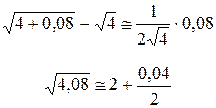
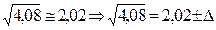 ,
, и существует
и существует 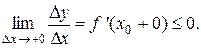
 и существует
и существует 
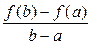 .
.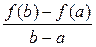 .
.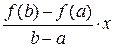 .
.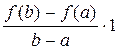 .
.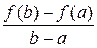 = 0, если f '(х 0) =
= 0, если f '(х 0) = 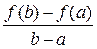 .
.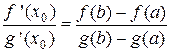 .
.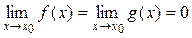 или
или 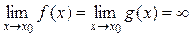 ,
,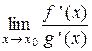 конечный или бесконечный, то выполняется равенство:
конечный или бесконечный, то выполняется равенство: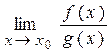 =
= 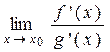 .
.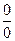 или
или 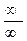 , возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞, 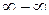 , 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к
, 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к 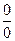 или
или 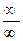 и тогда можно применить правило Лопиталя.
и тогда можно применить правило Лопиталя.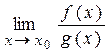 =
= 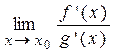 =
= 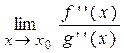
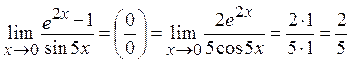
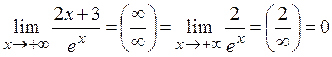
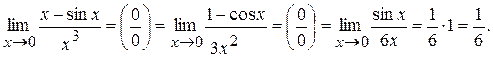
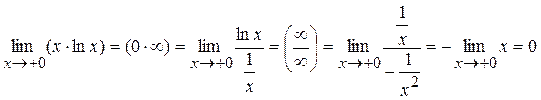 .
.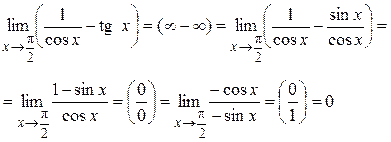
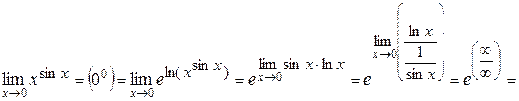
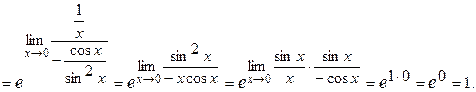
 или
или 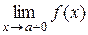 равен +¥ или – ¥.
равен +¥ или – ¥.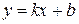 называется наклонной асимптотой кривой
называется наклонной асимптотой кривой 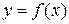 при
при 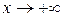 (или
(или 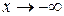 ), если функцию f (x) можно представить в виде:
), если функцию f (x) можно представить в виде: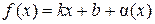 ,
,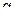 (x) – бесконечно малая функция при
(x) – бесконечно малая функция при 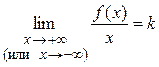 и
и 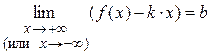
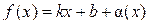 , где
, где 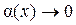 при
при 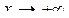 .
.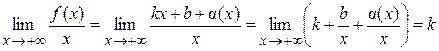 .
.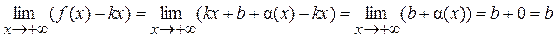 .
.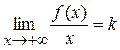 и
и 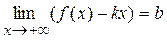 .
.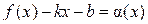 ,
, 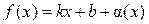 ,
,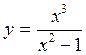 .
.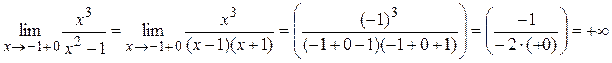
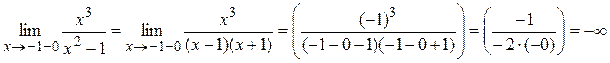
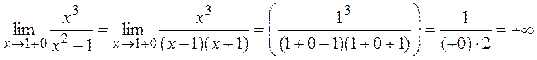
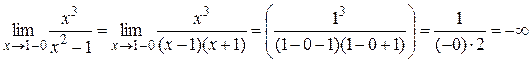
 , k = 1.
, k = 1.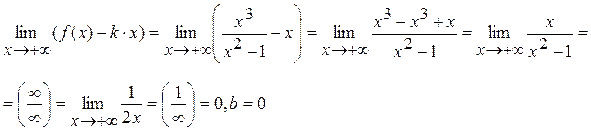
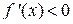 для любых
для любых 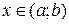 , то
, то 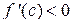 . Поэтому
. Поэтому 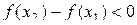 , то есть из условия x 2 > x 1 следует неравенство f (x 2) < f (x 1). Так как x 1 и x 2 любые значения из промежутка (a; b), то функция y = f (x) убывает на этом промежутке.
, то есть из условия x 2 > x 1 следует неравенство f (x 2) < f (x 1). Так как x 1 и x 2 любые значения из промежутка (a; b), то функция y = f (x) убывает на этом промежутке.


