
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл метода Гаусса
Метод Гаусса имеет определенный физический смысл. Посмотрим, например, чем отличаются друг от друга исходная система
и система
После исключения Если вспомнить исходную электросхему, то получается, что мы изымаем узел 1 и все ведущие к нему ветви Если к исключаемому узлу 1 был подведен ток извне (граничное условие 2-го рода, правая часть ненулевая), то после исключения неизвестного В конце прямой прогонки вся электрическая цепь будет заменена одним эквивалентным сопротивлением и можно будет найти силу тока в нем и разность потенциалов на его концах. Важной особенностью описанного алгоритма является то, что в ходе исключения неизвестных не происходит заполнения ленточной матрицы (появления ненулевых коэффициентов за пределами ленты там, где изначально были нули), и значит, для нулевых коэффициентов можно совсем не отводить память. Симметрия матрицы также сохраняется, т. е. вторую половину заполненной ленты также не нужно хранить.
12.8. Погрешность решения Подставив При сложении нескольких чисел, сильно различающихся по значению, результат зависит от порядка действий. Предположим, имеется 10 миллионов одинаковых малых чисел (равных 0.1) и одно большое 1.234.567, отличающееся от них более, чем на 7 порядков. Если вначале сложить малые числа, получим миллион, тогда общая сумма составит 2.234.567. Если же вначале взять число 1.234.567, то, сколько ни прибавляй к нему по 0.1, оно останется без изменения, если результат хранится в формате с обычной точностью (восьмая цифра числа теряется).
Устойчивость решения В процедуре метода Гаусса есть операция деления каждого уравнения на первый коэффициент. Вначале первое уравнение делят на Этого можно избежать, переставляя местами уравнения. Если сперва исключить то неизвестное, при котором диагональный коэффициент Понятие вырожденной матрицы поясняет рис. 12.4, где рассмотрено решение системы из двух уравнений, каждое уравнение изображается прямой линией на графике, по осям которого отложены значения неизвестных. Решение отображает точка пересечения прямых. Если матрица близка к вырожденной (ее определитель близок к нулю), то прямые пересекаются под острым углом. Это не мешает найти решение при отсутствии погрешностей в значениях коэффициентов матрицы и процедуре решения. Однако появление данных погрешностей, даже небольших, (на рисунке это показано заменой прямых на полосы, ширина которых характеризует погрешность) приводит к резкому увеличению погрешности результата решения. Причинами вырождения матрицы могут быть особенности геометрии модели, свойств материала и граничных условий. У вырожденной матрицы (определитель равен нулю) линии становятся параллельными (решение отсутствует) или совпадают (бесчисленное множество решений).
Рис. 12.4. Схема роста погрешности решения при вырождении матрицы
Итерационные методы решения Возможны два пути применения итераций при решении системы уравнений. I. Итерационное решение системы уравнений (применяется вместо метода Гаусса). Порядок итераций такой (см. схему на рис. 12.3):
1) Задаемся начальными значениями потенциала в точках 1, 2, 3 …, например 2) Проводим итерационное уточнение значений потенциала, для этого обходим по очереди все точки модели: - у точки 1 в уравнение постоянства заряда входят значения в точках со второй по пятую; поскольку все они имеют нулевой потенциал, значение в точке 1 после первой итерации не изменится: - у точки 2 среди соседей есть точки A и B, потенциалы которых - пройдя по остальным точкам, убедимся, что в них потенциал не изменится: 3) Теперь будем считать - в точке 1 потенциал изменится - в точке 2 потенциал не изменится - из остальных точек потенциал изменится в точке 3 4) Такой перебор всех точек будем повторять, пока хотя бы в одной из них будет происходить изменение потенциала. Итерации прекращаются, когда эти изменения за итерацию станут меньше заданного уровня точности
Достоинствами этого метода являются простота (уравнения составляются и решаются поочередно, полная система уравнений не составляется) и устойчивая сходимость при любом числе неизвестных. Его недостаток необходимость многократных обходов и медленная сходимость (особенно вначале, если исходное приближение выбрано неудачно). Разновидностью данного метода является метод Зейделя, в котором применение найденных значений неизвестных производится сразу, а не со следующей итерации. II. Итерационное уточнение решения, полученного методом Гаусса. Чтобы организовать итерационный процесс, нужно представить искомое значение на итерации в виде суммы значения на предыдущей итерации и приращения за итерацию:
Подставив это выражение в систему уравнений (12.7), получим:
Это система уравнений относительно Ход итерационного процесса такой: 1) Задаемся начальными значениями потенциала 2) Находим из решения системы (12.13) 3) Если после подстановки этих значений в исходные уравнения (12.7) получаем тождества, то найденные значения являются точными, и итерации прекращаются. Если же невязка 4) Условием завершения итераций является уменьшение до заданного порога либо невязки
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.184 (0.012 с.) |

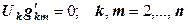 .
. элементы матрицы
элементы матрицы  , исчезают, а остальные элементы изменяются
, исчезают, а остальные элементы изменяются 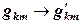 , при этом все
, при этом все 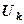 в двух системах одинаковые при
в двух системах одинаковые при  .
.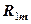 , а чтобы потенциалы в остальных точках не изменились, пускаем те токи, которые шли через узел 1, по соседним ветвям, скорректировав для этого их проводимость
, а чтобы потенциалы в остальных точках не изменились, пускаем те токи, которые шли через узел 1, по соседним ветвям, скорректировав для этого их проводимость 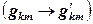 .
. появятся ненулевые правые части у соседних уравнений, т. е. этот внешний ток будет перераспределен на соседние узлы.
появятся ненулевые правые части у соседних уравнений, т. е. этот внешний ток будет перераспределен на соседние узлы. в исходные уравнения, мы получим числа, отличающиеся от правых частей этих уравнений. Это означает, что решение имеет погрешность. Основная причина – ограниченная точность расчетов. Компьютер хранит каждое число в виде 7 десятичных цифр при обычной точности (4 байта на одно число) и 15 цифр - при двойной точности (8 байт на одно число).
в исходные уравнения, мы получим числа, отличающиеся от правых частей этих уравнений. Это означает, что решение имеет погрешность. Основная причина – ограниченная точность расчетов. Компьютер хранит каждое число в виде 7 десятичных цифр при обычной точности (4 байта на одно число) и 15 цифр - при двойной точности (8 байт на одно число).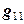 , потом второе на
, потом второе на 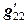 и т. д, но
и т. д, но  (если
(если  ). По мере исключения неизвестных коэффициенты на главной диагонали
). По мере исключения неизвестных коэффициенты на главной диагонали 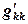 уменьшаются, и к тому моменту, когда происходит деление, может произойти уменьшение
уменьшаются, и к тому моменту, когда происходит деление, может произойти уменьшение  , и после деления на нуль решение полностью нарушается. Иногда получается не 0, а просто большой рост погрешности.
, и после деления на нуль решение полностью нарушается. Иногда получается не 0, а просто большой рост погрешности.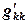 самый большой, то из других уравнений будут вычитаться маленькие числа и устойчивость решения повысится. К счастью, в большинстве случаев матрица
самый большой, то из других уравнений будут вычитаться маленькие числа и устойчивость решения повысится. К счастью, в большинстве случаев матрица  оказывается положительно-определенной и невырожденной, т. е. решение идет устойчиво без дополнительных усилий.
оказывается положительно-определенной и невырожденной, т. е. решение идет устойчиво без дополнительных усилий.
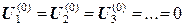 (кроме А, В,…, в которых потенциал известен).
(кроме А, В,…, в которых потенциал известен). ;
; и
и 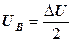 известны, а
известны, а 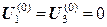 , по этим данным из уравнения постоянства заряда можно найти
, по этим данным из уравнения постоянства заряда можно найти  ;
;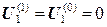 .
.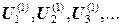 новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала:
новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала: , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;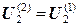 , поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3;
, поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3; , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.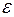 :
:
 . (12.12)
. (12.12) ;
;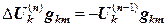 . (12.13)
. (12.13) , аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.
, аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.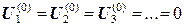 .
. , затем
, затем  по формуле (12.12).
по формуле (12.12).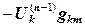 ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных
ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных  , чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).
, чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).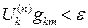 , либо приращения за шаг
, либо приращения за шаг  .
.


