
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение сохранения заряда. Первое правило Кирхгофа
В основе решения задачи лежит уравнение сохранения заряда. Заряд не накапливается в участках электрической цепи, поэтому сумма токов, втекающих в каждый узел, равна нулю (первое правило Кирхгофа)
Например, для узла 1
где Мы получили уравнение (12.5), в котором несколько неизвестных – потенциал узла 1 и смежных с ним узлов 2, 3, 4 и 5. Это - уравнение постоянства заряда в узле 1. Такое уравнение можно записать для каждого узла, поэтому число уравнений равно общему количеству неизвестных. Вместе они образуют систему линейных уравнений:
которая в сокращенной (тензорной) форме записи выглядит как
где Мы проследили всю типичную процедуру метода конечных элементов от вывода исходных уравнений на основе некоторого дифференциального уравнения до сведения их в систему линейных уравнений. Далее необходимо решить систему и найти неизвестные, а по ним – все остальные параметры модели. В данном случае исходное дифференциальное уравнение сохранения заряда – это уравнение Лапласа (12.2). Его можно превратить в систему алгебраических уравнений, если вместо производных подставить отношение конечных разностей:
Можно сказать, что каждое уравнение в системе (12.6) – это проинтегрированное по некоторой области (по одной ячейке) дифференциальное уравнение (12.2). При интегрировании появляются неопределенные константы, которые нужно установить из граничных условий для получения окончательного решения. Граничными условиями являются значения функции в соседних узлах. Смысл системы уравнений заключается в стыковке между собой полученных интегралов по всем ячейкам. Свойства системы уравнений Матрица
В каждой строке данной матрицы самый большой коэффициент находится на главной диагонали, и он положителен. Остальные коэффициенты отрицательны и меньше по абсолютной величине. Сумма коэффициентов в каждой строке равна нулю. Действительно, если потенциалы смежных ячеек равны
то все токи будут равны нулю. Подставим (12.8) в уравнение (12.5)
откуда
Таким образом, матрица является положительно определенной. Это обеспечивает устойчивость решения системы методом Гаусса. Матрица разреженная, в ней много нулевых коэффициентов: Очень важным моментом является однородность системы уравнений (в правой части - нули). Это значит, что она всегда имеет решение Возможно, система имеет также нетривиальное решение с разными Если в другом узле Условием 2-го рода является подача тока от внешнего источника в какой-то из узлов. Этот ток добавляется к правой части соответствующего уравнения.
|
|||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.19.251 (0.005 с.) |
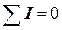 . (12.4)
. (12.4)
 ;
; ;
; ;
; , (12.5)
, (12.5)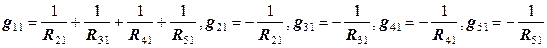 .
.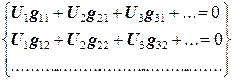 , (12.6)
, (12.6)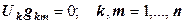 , (12.7)
, (12.7)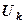 - вектор неизвестных потенциалов в узлах,
- вектор неизвестных потенциалов в узлах,  - матрица
- матрица  системы уравнений,
системы уравнений,  - порядок матрицы (число неизвестных и уравнений в системе). При тензорной записи пропускают знак суммы. На то, что в выражении (12.7) записан не одночлен, а сумма одночленов, указывает «слепой» - повторяющийся два раза индекс k, по которому и производят суммирование.
- порядок матрицы (число неизвестных и уравнений в системе). При тензорной записи пропускают знак суммы. На то, что в выражении (12.7) записан не одночлен, а сумма одночленов, указывает «слепой» - повторяющийся два раза индекс k, по которому и производят суммирование. .
. традиционно называется матрицей жесткости (потому что МКЭ создавали для задач механики), но в данном случае это матрица проводимости
традиционно называется матрицей жесткости (потому что МКЭ создавали для задач механики), но в данном случае это матрица проводимости  . Эта матрица симметричная:
. Эта матрица симметричная: .
. , (12.8)
, (12.8) ,
,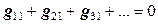 ,
, .
.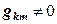 только если узлы
только если узлы 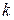 и
и  - смежные. Если удачно пронумеровать узлы, то ненулевые элементы соберутся в ленту около главной диагонали (получим ленточную матрицу). Остальные элементы можно не хранить, т. е. экономить память компьютера. Кроме того, вследствие симметрии матрицы достаточно хранить только половину ленты.
- смежные. Если удачно пронумеровать узлы, то ненулевые элементы соберутся в ленту около главной диагонали (получим ленточную матрицу). Остальные элементы можно не хранить, т. е. экономить память компьютера. Кроме того, вследствие симметрии матрицы достаточно хранить только половину ленты.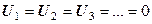 . Кроме того, мы установили, что
. Кроме того, мы установили, что  также будет решением при любом
также будет решением при любом 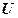 . Такие решения называются тривиальными.
. Такие решения называются тривиальными.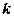 . Для этого нужно исключить из системы одно уравнение (поскольку значение в одном из узлов известно) или заменить его (что то же самое) на
. Для этого нужно исключить из системы одно уравнение (поскольку значение в одном из узлов известно) или заменить его (что то же самое) на  (см. рис. 12.2). После этой процедуры система перестает быть однородной (в остальных уравнениях появится правая часть
(см. рис. 12.2). После этой процедуры система перестает быть однородной (в остальных уравнениях появится правая часть 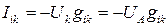 ). Если других условий нет, то решение системы уравнений даст во всех узлах одинаковый потенциал
). Если других условий нет, то решение системы уравнений даст во всех узлах одинаковый потенциал 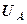 .
. , получим разные потенциалы во всех узлах.
, получим разные потенциалы во всех узлах.


