
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.3. Проекции вектора. Расположение вектора в пространстве. Операции над векторами.
Определение 19. Проекцией вектора
Свойство 1. Свойство 2. Свойство 3. Определение 20. Проекции вектора на координатные оси называются координатами вектора.
Если даны координаты точек A (x 1, y 1, z 1), B (x 2, y 2, z 2), то
Длина вектора находится по формуле:
Вектор Ортами координатных осей (Ох), (О y), (О z) называются векторы
Так как
Пример. Найти разложение вектора Решение. 1) Разложение вектора 2) Векторы
Следовательно, Проиллюстрируем пример. Изобразим векторы на плоскости.
По правилу параллелограмма найдем сумму двух векторов
Пусть α, β, γ – углы между вектором Определение 21. Направляющими косинусами вектора
Направляющие косинусы являются координатами орта вектора Определение 22. Орт вектора называется нормированным вектором. Определение 23. Даны два вектора
Определение 24. Произведением вектора Замечание. Для вектора Пример. Даны точки М 1(2; 1), М 2(–1;3) и вектор Решение. Найдем координаты вектора
Найдем направляющие косинусы: Координаты орта: Проверим коллинеарность векторов: для коллинеарности должно выполняться условие Найдем координаты вектора
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.86.155 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||
 на ось l называется число – длина вектора
на ось l называется число – длина вектора 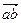 этой оси, заключенного между проекциями a и b его начальной точки А и конечной точки В, взятая со знаком «плюс», если направление
этой оси, заключенного между проекциями a и b его начальной точки А и конечной точки В, взятая со знаком «плюс», если направление 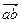 совпадает с направлением оси l, и со знаком «минус», если эти направления противоположны.
совпадает с направлением оси l, и со знаком «минус», если эти направления противоположны.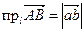
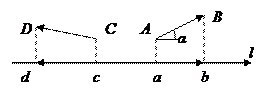 ,
, 
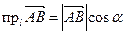 , где α – угол между вектором
, где α – угол между вектором 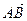 и положительным направлением оси l.
и положительным направлением оси l.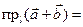

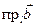 . Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.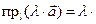

 , где
, где 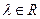 .
.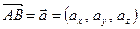 ,
,  координаты вектора
координаты вектора 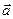 .
.
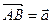

 .
. коллинеарен вектору
коллинеарен вектору 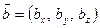 тогда и только тогда, когда их координаты пропорциональны:
тогда и только тогда, когда их координаты пропорциональны:  , где λ – коэффициент пропорциональности. Если λ > 0, векторы сонаправлены (
, где λ – коэффициент пропорциональности. Если λ > 0, векторы сонаправлены (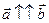 ); λ < 0, векторы противоположно направлены (
); λ < 0, векторы противоположно направлены ( ).
).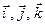 соответственно.
соответственно.  .
. Рассмотрим радиус-вектор
Рассмотрим радиус-вектор 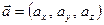 , построенный на векторах
, построенный на векторах  (по правилу параллелепипеда), причем
(по правилу параллелепипеда), причем 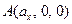 ,
,  ,
, 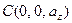 :
:  (*).
(*).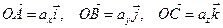 , то, подставив в (*), получим
, то, подставив в (*), получим разложение вектора
разложение вектора 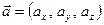 по ортам
по ортам  (разложением по базису).
(разложением по базису). 1) по базису векторов
1) по базису векторов 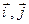 , 2) по базису векторов
, 2) по базису векторов 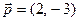 и
и  .
.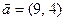 по базису векторов
по базису векторов 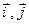 имеет вид:
имеет вид:  .
.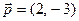 и
и  не коллинеарны, так как
не коллинеарны, так как 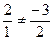 , следовательно, образуют базис. Вектор
, следовательно, образуют базис. Вектор 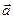 представляет собой линейную комбинацию векторов
представляет собой линейную комбинацию векторов 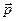 и
и  :
:  , где числа х и у – коэффициенты линейной комбинации. Найдем их. Для этого составим систему:
, где числа х и у – коэффициенты линейной комбинации. Найдем их. Для этого составим систему: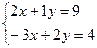
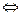
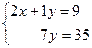 . Отсюда у = 5, х = 2.
. Отсюда у = 5, х = 2.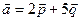 - разложение вектора
- разложение вектора  .
.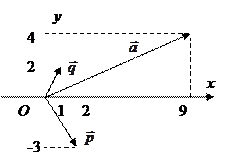
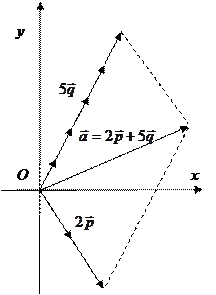









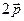 и
и 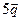 :
: и координатными осями, тогда в силу свойства 1 получим, что
и координатными осями, тогда в силу свойства 1 получим, что 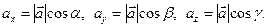
 называются
называются  , где α, β, γ – углы между вектором
, где α, β, γ – углы между вектором 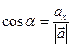 ,
,  ,
,  .
. .
. ,
, 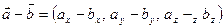 .
. такой, что
такой, что 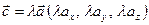 .
. n -мерного пространства справедливы все определения и теоремы.
n -мерного пространства справедливы все определения и теоремы. . Найти длину и направляющие косинусы вектора
. Найти длину и направляющие косинусы вектора 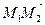 , координаты его орта, проверить коллинеарность векторов
, координаты его орта, проверить коллинеарность векторов 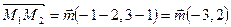 .
.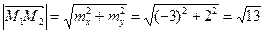 .
.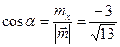 ,
,  .
. . Вектор называется нормированным вектором.
. Вектор называется нормированным вектором. . Проверим:
. Проверим: 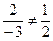 , следовательно,
, следовательно,  и
и 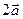 найдем по определению 24:
найдем по определению 24:  , тогда по определению 23:
, тогда по определению 23:  – 2
– 2  .
.


