
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило решения произвольной системы линейных уравнений
1. Вычисляем ранг основной и расширенной матрицы и решаем вопрос о совместности системы. Если система совместна, то находим какой-либо базисный минор M порядка r. 2. Берем r уравнений, из коэффициентов которых составлен базисный минор, остальные уравнения отбрасываем. Неизвестные, коэффициенты которых составляют базисный минор, считаем главными и оставляем слева. Остальные n – r неизвестных считаем свободными и переносим в правые части уравнений. 3. По правилу Крамера находим выражения главных неизвестных через свободные. Полученные равенства являются общим решением системы. 4. Придавая свободным неизвестным любые числовые значения, находим соответствующие значения главных неизвестных, т.е. частные решения системы. Пример. Решить систему:
1)
В качестве базисного минора возьмем определитель 2) Отбросим третье уравнение системы, получим систему двух уравнений:
В которой неизвестные 3) Решим эту систему по формулам Крамера:
отсюда, 4) Подставляя полученные выражения для
Ответ: общее решение: Пп. 2. Метод Гаусса Решение неоднородных систем Одним из наиболее универсальных и эффективных методов решения линейных алгебраических систем является метод Гаусса, который состоит в последовательном исключении неизвестных. Пусть дана система неоднородных уравнений
Процесс решения состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
где На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы. Прямой ход: Будем считать, что элемент Преобразуем систему, исключив неизвестное
Здесь Аналогичным образом, считая главным элементом Если в процессе решения появляются нулевые уравнения, т.е. уравнения вида Обратный ход заключается в решении ступенчатой системы уравнений, которая, вообще говоря, имеет бесконечное множество решений. В последнем уравнении выражаем первое неизвестное Замечание 1. Если ступенчатая система оказывается треугольной, т.е. Замечание 2. На практике удобнее работать не с системой, а с расширенной матрицей системы (пример см. в методичке Парыгина и др. ч.2, стр. 13).
|
|||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.90.131 (0.008 с.) |

 ,
,  ;
; ,
, 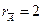 , следовательно, система совместна.
, следовательно, система совместна. ,
,
 и
и  – главные а
– главные а 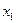 и
и  – свободные.
– свободные. ,
, ,
, 
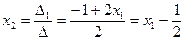 ,
,  .
.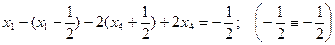 .
. , частное решение при
, частное решение при  ,
,  :
:  .
.

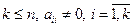 . Коэффициенты
. Коэффициенты  называют главными коэффициентами системы.
называют главными коэффициентами системы. ; (если
; (если  , то первым в системе запишем то уравнение, в котором коэффициент при
, то первым в системе запишем то уравнение, в котором коэффициент при 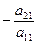 и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 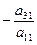 и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
 ,
, 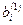
 – новые значения коэффициентов и правых частей, которые получаются после первого шага.
– новые значения коэффициентов и правых частей, которые получаются после первого шага. , исключим неизвестное
, исключим неизвестное  из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока возможно.
из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока возможно.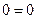 , их отбрасывают. Если же появляются уравнения
, их отбрасывают. Если же появляются уравнения  , а
, а 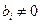 , то это говорит о том, что система несовместна.
, то это говорит о том, что система несовместна.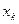 через остальные неизвестные
через остальные неизвестные  . Затем подставляем значение
. Затем подставляем значение 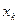 в предпоследнее уравнение системы и выражаем
в предпоследнее уравнение системы и выражаем  через
через  , то система имеет единственное решение.
, то система имеет единственное решение.


