
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические модели и характеристики
В зависимости от характера информационного параметра сообщения могут быть непрерывными и дискретными (рис.1). Если информационный параметр сообщения может принимать любое значение в некотором интервале, то сообщение называется непрерывным. В этом смысле звуковые колебания, соответствующие речи - типичный пример непрерывного сообщения. Конечность числа возможных значений информационного параметра является признаком дискретного сообщения. Любой текст на русском языке можно записать с помощью 33 букв и нескольких знаков препинания, т.е. число значений информационного параметра текстового сообщения конечно. Таким образом, текст - дискретное сообщение.
Дискретные сообщения состоят из отдельных знаков, комбинируемых определенным образом. Типичным примером дискретного сообщения является текст, состоящий из букв и знаков препинания. Поскольку все возможные знаки сообщений заранее известны, то нет необходимости передавать на приемную сторону сами знаки, а достаточно передавать информацию о том, какой знак из известного набора необходимо взять в каждом случае. Например, вместо букв можно передавать их порядковые номера, присвоив предварительно каждой букве определенный номер. Для этого все возможные буквы (знаки сообщений) располагают последовательно и нумеруют, как показано в таблице на примере русского алфавита. На приемной стороне число (порядковый номер) позволяет определить по таблице соответствующую букву.
В таблице порядковые числа приведены в десятичной, пятеричной и двоичной системах счисления. Если вместо 32 букв русского алфавита (без буквы ё) передавать по системе связи их порядковые номера в виде чисел в десятичной системе счисления, то всего потребуется передавать десять различных цифр. При использовании пятеричной системы число передаваемых цифр уменьшается до пяти. Двоичная система счисления позволяет уменьшать число передаваемых цифр до двух. Это очень важное обстоятельство, позволяющее значительно упростить устройства передачи дискретных сообщений. В современных системах связи используют, как правило, двоичные системы счисления. Таким образом, вместо знаков сообщений передают их условные обозначения, представляющие собой комбинацию цифр 0 и 1. Эти комбинации принято называть кодовыми комбинациями, а отдельные цифры (0 и 1), входящие в комбинацию – элементами. Совокупность всех кодовых комбинаций и соответствующие им знаки сообщения образуют код.
Пример записи слова «Родина» пятиэлементным двоичным кодом (по данным табл.) показан на рис. 2.
Как видно из рисунка, слово «Родина», состоящее из шести различных букв, превратилось в последовательность двух элементов 0 и 1. Символы 0 и 1 могут передаваться по каналу связи электрическими импульсами различной амплитуды или полярности. Процесс преобразования знаков сообщения в кодовые комбинации называют кодированием. Правило кодирования (код) обычно представляют в виде таблиц. На практике для первичного кодирования дискретных сообщений широко используются различные коды, например: МТК-2 (международный телеграфный код), КОИ-7, КОИ-8 (коды обмена информацией) и др. Как было отмечено на прошлой лекции, для получателя информации передача какого-либо частного сообщения всегда представляет собой случайный выбор из некоторого заданного множества сообщений подобно тому, как если бы получатель имел дело с некоторой случайной величиной, закон распределения которой совпадает с законом распределения сообщений. Простейшей статистической моделью дискретного сообщения является дискретная случайная величина. Модели сообщений и их характеристики, основанные на теории вероятностей и математической статистике, называют статистическими. Как и любая наука, теория вероятностей опирается на ряд основных понятий, которые нельзя строго определить, а можно только пояснить. К таким понятиям относятся: событие, вероятность события, частота события, случайная величина и т.д. Математическая статистика – наука о математических методах, позволяющих по статистическим данным (реализациям сл. в. и случайных процессов) строить теоретико-вероятностную модель исследуемого явления. В некотором смысле задачи математической статистики являются обратными по отношению к задачам теории вероятностей. Случайной величиной (сл.в.) называется величина, которая в результате опыта может принять то или иное, заранее неизвестное, значение.
Существует другое определение. Сл.в. - это функция, отображающая пространство элементарных событий в множество чисел, т.е. она является числовой функцией, аргументом которой являются исходы случайного опыта. Для сл.в. можно указать только значения, одно из которых она обязательно примет в результате опыта. Эти значения называют возможными значениями сл.в. Случайные величины обозначаются малыми буквами греческого алфавита x, h, g, …, или заглавными буквами латинского алфавита X, Y, Z, …, а их возможные значения (реализации) – малыми буквами латинского алфавита x, y, z, … Далее сл.в. обозначаются малыми буквами греческого алфавита. В зависимости от возможных значений и характера закона распределения сл.в. делятся на дискретные, непрерывные и смешанные (непрерывно-дискретные). Дискретной сл.в. называется такая величина, которая может принимать конечное или бесконечное счетное множество значений - их можно пронумеровать. Чтобы определить (задать) обычную переменную величину достаточно указать множество ее возможных значений. Для описания сл.в. нужно указать все ее возможные значения и вероятности этих значений, т.е. иметь закон распределения вероятностей сл.в. Законом распределения (з.р.) вероятностей сл.в. называется всякое соотношение, устанавливающее связь между ее возможными значениями и вероятностями этих значений. Иначе говоря, это всякая характеристика, которая определяет способ распределения полной (единичной) вероятности между отдельными возможными значениями или группами возможных значений. З.р. дает полное описание сл.в. Зная его, можно до опыта (априорно) указать, где располагаются возможные значения сл.в.: какова вероятность появления сл.в. в том или ином интервале; какие возможные значения сл.в. будут появляться чаще, а какие - реже. Пример априорного задания ансамбля дискретных сообщений: определяем дискретную случайную величину Применительно к передаче дискретных сообщений под опытом можно понимать передачу конкретного частного сообщения. Качественной характеристикой случайного результата опыта является событие, например, при передаче текста передана буква А. Для более глубокого, количественного описания случайных явлений исходы опытов оцениваются числами. В приведённом примере передаче буквы А можно сопоставить десятичное число 0. Совокупность таких чисел образует случайную величину. Можно определить события, заключающиеся в том, что случайная величина приняла конкретное числовое значение.
 события события 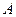 . .
Вероятность конкретного значения случайной величины равна вероятности соответствующего события. Под вероятностью события понимают число, которое характеризует степень объективной возможности появления этого события. Иначе говоря, вероятность это численная мера степени объективной возможности события.
Исчерпывающей математической формулировки понятия вероятности не существует. Однако существуют два частных, но очень важных для практики определения, а именно, статистическое и классическое определения вероятности. Классическое определение вероятности нам потребуется на практическом занятии по расчёту статистических характеристик передаваемых дискретных сообщений. Классическое (иначе математическое, теоретическое) определение вероятности опирается на понятие равновозможных событий, вводимое без доказательства. Оно оправдано тогда, когда существует возможность предсказания вероятности на основании симметрии условий, при которых происходит испытание и, вследствие этого, симметрии исходов испытания, что и приводит к представлению о «равновозможности». Рассмотрим опыт с N равновозможными исходами, которые несовместны и составляют полную группу (схема случаев). Пусть событию А благоприятствует (влечет за собой выполнение события А) n случаев. Вероятностью Р(А) события А называется отношение числа случаев n, благоприятствующих появлению события А, к общему числу равновозможных случаев N: P (A)= n / N.
Для непосредственного вычисления вероятностей по классическому определению необходимо: выявить число N несовместных, равновозможных исходов, составляющих полную группу; найти число n случаев, благоприятствующих событию А; вычислить вероятность Р(А). Для облегчения вычислений широко используются формулы комбинаторики (теории соединений): размещений, перестановок, сочетаний. Применение статистического определения для нахождения вероятностей появления букв русского языка в тексте показывает, что наиболее часто в достаточно длинных текстах литературного русского языка встречается буква О, вероятность которой равна 0,089. Реже других встречается буква Ф, которой соответствует вероятность 0,002.
Таблица 2
На практике между передаваемыми символами всегда существует связь. Например, при передаче текста причина этого лежит в структуре языка. В большинстве реальных случаев появление в последовательности элемента Процесс называется стационарным, если для любых Простейшей моделью источника, порождающего зависимые сообщения, является марковский источник. Случайный процесс
Иными словами, мы называем марковским процессом связности s такой процесс, для которого при
то есть условная вероятность текущего значения при известных предшествующих s не зависит от всех других предшествующих значений. Значение марковского процесса Однородная марковская цепь связности
называемые переходными вероятностями цепи Маркова. Переходные вероятности удобно записывать в виде квадратной матрицы размерности
называемой матрицей переходных вероятностей. Эта матрица - стохастическая (неотрицательная, сумма элементов каждой строки равна 1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.111.233 (0.029 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


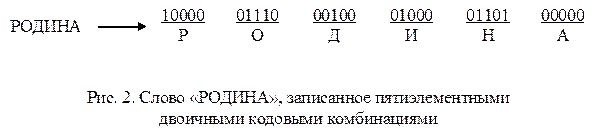
 и вероятности её возможных значений
и вероятности её возможных значений  ,
,  , …,
, …,  ,
,  .
. зависит от того, какой элемент
зависит от того, какой элемент  был предшествующим. Поэтому кроме простейшей (дискретная случайная величина) в качестве математической модели дискретных сообщений используют марковские случайные дискретные последовательности или цепи, у которых статистическая связь распространяется только на два и более соседних элемента. Чтобы отразить факт зависимости символов в сообщении вводится условная вероятность
был предшествующим. Поэтому кроме простейшей (дискретная случайная величина) в качестве математической модели дискретных сообщений используют марковские случайные дискретные последовательности или цепи, у которых статистическая связь распространяется только на два и более соседних элемента. Чтобы отразить факт зависимости символов в сообщении вводится условная вероятность  , показывающая вероятность появления символа
, показывающая вероятность появления символа  со значениями
со значениями  ,
,  , задан, если для любых
, задан, если для любых  указан способ вычисления совместных распределений вероятностей
указан способ вычисления совместных распределений вероятностей  .
.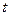 имеет место равенство
имеет место равенство  . Иными словами, случайный процесс стационарен, если вероятность любой последовательности не изменяется при ее сдвиге во времени (не зависит от положения последовательности на оси времени).
. Иными словами, случайный процесс стационарен, если вероятность любой последовательности не изменяется при ее сдвиге во времени (не зависит от положения последовательности на оси времени). справедливы соотношения
справедливы соотношения .
.
 ,
,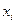 в момент времени t принято называть состоянием в момент t Описание марковского процесса задается начальным распределением вероятностей на последовательностях из первых s значений (состояний) и условными вероятностями вида
в момент времени t принято называть состоянием в момент t Описание марковского процесса задается начальным распределением вероятностей на последовательностях из первых s значений (состояний) и условными вероятностями вида  для всевозможных последовательностей
для всевозможных последовательностей 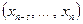 . Если указанные условные вероятности не изменяются при сдвиге последовательностей
. Если указанные условные вероятности не изменяются при сдвиге последовательностей  во времени, марковская цепь называется однородной.
во времени, марковская цепь называется однородной. называется простой цепью Маркова. Для описания простой цепи Маркова с множеством состояний
называется простой цепью Маркова. Для описания простой цепи Маркова с множеством состояний  достаточно указать начальное распределение вероятностей
достаточно указать начальное распределение вероятностей 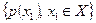 и условные вероятности
и условные вероятности ,
,  ,
,




