
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.3. От тригонометрической функции. ⇐ ПредыдущаяСтр 7 из 7
Задача 72. Вычислить интеграл Решение. Тогда вынесем за знак интеграла все константы, получим
Надо умножить каждую на каждую, лучше всего их все учесть с помощью такой таблицы.
что далее можно представить в виде суммы 5 интегралов. Для 1-го и 2-го из них функции вообще не имеет особых точек внутри круга радиуса 1, эти слагаемые 0. Исследуем 3 последних.
Задача 73. Вычислить интеграл Решение. Здесь надо сделать замену
Теперь найдём корни многочлена в знаменателе, тем самым найдём полюсы функции.
С учётом найденных полюсов, интеграл запишется в виде:
Задача 74. Вычислить Решение.
Один полюс внутри круга, другой снаружи, таким образом, надо будет считать только один вычет в точке
Задача 75. Вычислить интеграл Решение. Чтобы упростить это выражение, сначала домножим на
Отдельный множитель Итак, получили
Итак, 2 из 3 полюсов внутри круга радиуса 1, т.е. интеграл определяется суммой вычетов в них.
Подынтегральную функцию можно представить в виде:
Итак, мы должны вычислить
Для сравнения, покажем решение этой задачи методами прошлого семестра, без вычетов. Можно было применить универсальную тригонометрическую подстановку, но лучше подвести под знак дифференциала.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 76; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.12 (0.012 с.) |
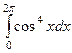 .
.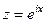 ,
, 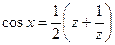 ,
, 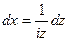 .
.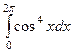 =
= 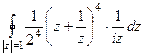 ,
,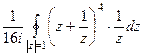 =
= 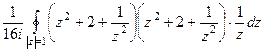 =
=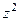
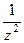
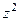
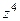
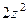
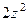
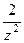
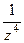
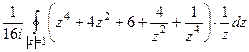 =
= 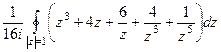
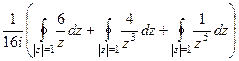 , каждый считается с помощью вычета внутри круга, причём для всех полюс это точка
, каждый считается с помощью вычета внутри круга, причём для всех полюс это точка 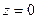 . Но в одном случае это полюс 1 порядка, а в других 3-го и 5-го. Если полюс кратный, то находится производная от числителя, а он равен константе, значит, производная равна 0. Таким образом, два последних интеграла тоже 0.
. Но в одном случае это полюс 1 порядка, а в других 3-го и 5-го. Если полюс кратный, то находится производная от числителя, а он равен константе, значит, производная равна 0. Таким образом, два последних интеграла тоже 0.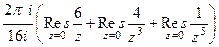 =
= 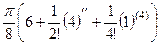 =
=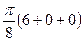 =
= 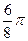 =
= 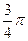 . Ответ.
. Ответ. 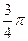 .
.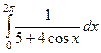 .
. 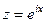 , при которой:
, при которой: 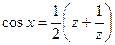 ,
, 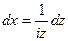 .
.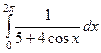 =
= 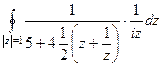 =
= 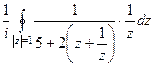 =
=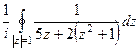 =
= 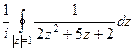 .
.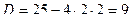 .
. 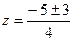 , корни
, корни 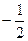 и
и 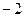 . Один из них, очевидно, внутри единичного круга, другой снаружи. Поэтому надо будет найти всего один вычет.
. Один из них, очевидно, внутри единичного круга, другой снаружи. Поэтому надо будет найти всего один вычет.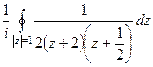 =
= 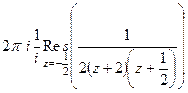 =
=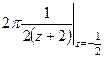 =
= 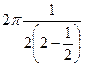 =
= 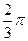 . Ответ.
. Ответ. 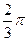 .
.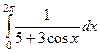 .
.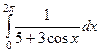 =
= 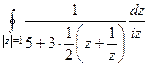 =
=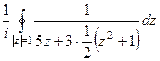 =
= 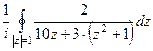 =
= 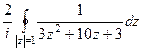 , далее найдём корни многочлена в знаменателе, это и будут полюсы функции.
, далее найдём корни многочлена в знаменателе, это и будут полюсы функции.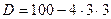 = 64,
= 64, 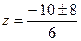 , т.е.
, т.е. 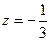 и
и 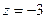 .
.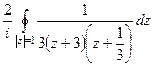 =
= 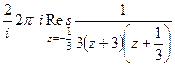 =
= 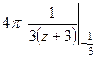 =
=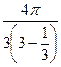 =
= 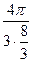 =
= 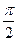 . Ответ.
. Ответ. 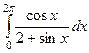 .
.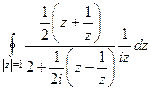
 в числителе и знаменателе, затем на 2, затем домножим
в числителе и знаменателе, затем на 2, затем домножим 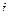 , которое есть в знаменателе, на все слагаемые слева от него.
, которое есть в знаменателе, на все слагаемые слева от него.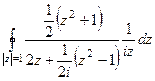 =
= 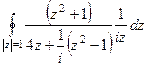 =
= 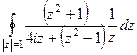
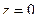 . Чтобы не приводить к 3-й степени и не усложнять поиск корней многочлена, лучше оставить это
. Чтобы не приводить к 3-й степени и не усложнять поиск корней многочлена, лучше оставить это  отдельно, и найти 2 корня многочлена второй степени.
отдельно, и найти 2 корня многочлена второй степени.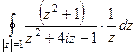 . Один полюс
. Один полюс 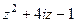 .
.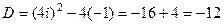 .
. 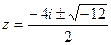 =
= 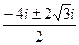 =
= 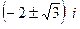 . При этом
. При этом 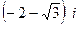 по модулю больше 1, т.е. этот полюс вне единичного круга, а точка
по модулю больше 1, т.е. этот полюс вне единичного круга, а точка 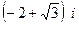 внутри круга.
внутри круга.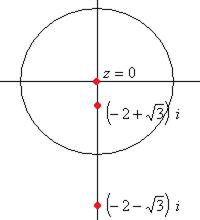
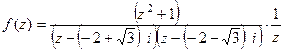 впрочем, когда мы будем считать вычет в 0, те две скобки можем для краткости опять объединить.
впрочем, когда мы будем считать вычет в 0, те две скобки можем для краткости опять объединить.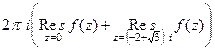 , причём полюсы 1-го порядка.
, причём полюсы 1-го порядка.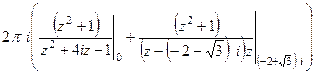 =
=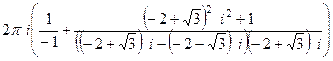 =
=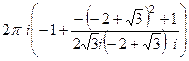 =
= 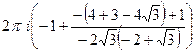 =
=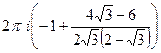 =
= 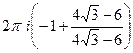 =
= 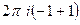 = 0.
= 0.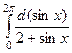 =
= 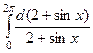 =
= 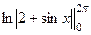 =
= 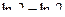 = 0. Ответ. 0.
= 0. Ответ. 0.


