
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 7 (неделя с 12 по 18 октября). Аудиторно.
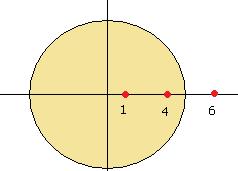
Задача 63. Вычислить вычет Решение. Здесь точка Тогда Приложения вычетов. П. 1. По замкнутому контуру. Задача 64. Вычислить интеграл Решение. Так как радиус равен 4,5 то точки 1 и 4 внутри круга, а 6 снаружи. Поэтому интеграл считается с помощью суммы двух вычетов, а не трёх.
Для технического удобства вычисления производной мы сначала перемножили в знаменателе, а потом снова разъединили множители. Ответ. Задача 65. Вычислить интеграл Решение. Здесь очевидно, точки 2 и 4 внутри круга, 6 снаружи, так как радиус равен 5.
Ответ. П. 2. По действительной оси. Задача 66. Вычислить интеграл Решение. Рассмотрим функцию
Таким образом,
Ответ. Задача 67. Вычислить интеграл Решение. Найдём корни знаменателя функции
В верхней полуплоскости только один полюс,
Ответ. Замечание. Для сравнения, покажем и решение методами прошлого семестра, без комплексных чисел и вычетов. Задача домашняя. Вычислить интеграл Указание. Корни Задача 68. Вычислить интеграл Решение. Корни
Ответ. Задача 69. Вычислить Решение. Для решения таких задач во 2 семестре требовалось использовать рекуррентную формулу, чтобы свести к меньшей степени. А с помощью вычетов, это не нужно, отличие лишь в том, что полюс 2-го порядка, и надо будет использовать обобщённую интегральную формулу Коши (с производной). Тот факт, что интеграл по полуоси, не существенен: мы можем, пользуясь чётностью функции, удвоить до интеграла по всей оси (а потом разделить на 2) то есть решить этим методом можно.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.102 (0.007 с.) |
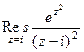 .
.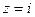 полюс 2-го порядка.
полюс 2-го порядка.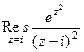 =
= 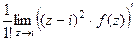 =
= 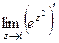 =
=  =
= 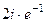 =
= 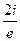 . Ответ.
. Ответ. 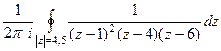 .
.
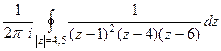 =
= 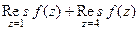 . Одна из точек (
. Одна из точек ( ) это полюс 2-го порядка, в том случае надо считать производную, а там где полюс 1-го порядка (
) это полюс 2-го порядка, в том случае надо считать производную, а там где полюс 1-го порядка (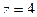 ) не нужно.
) не нужно.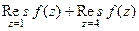 =
=  =
= =
=  =
=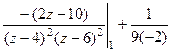 =
=  =
=  =
=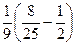 =
= 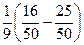 =
= 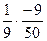 =
= 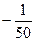 .
.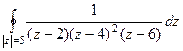 .
.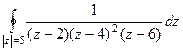 =
= 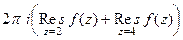 =
=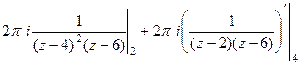 =
=  =
= =
= 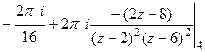 =
= 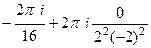 =
= 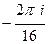 =
= 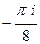 .
.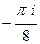 .
.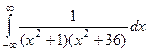 с помощью вычетов.
с помощью вычетов.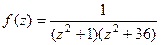 , её можно представить в виде
, её можно представить в виде 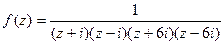 , есть 4 полюса первого порядка:
, есть 4 полюса первого порядка: 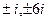 . Интеграл по границе верхнего полукруга равен сумме вычетов в 2 точках, а именно
. Интеграл по границе верхнего полукруга равен сумме вычетов в 2 точках, а именно 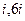 . Если радиус больше 6, то обе точки внутри полукруга, и при дальнейшем увеличении радиуса интеграл уже не изменится. При этом из теории известно, что при увеличении радиуса, доля результата, приходящегося на горизонтальный отрезок, растёт, а по дуге - стремится к 0, потому что здесь степень знаменателя на 4 больше, чем числителя, то есть модуль функции величина порядка
. Если радиус больше 6, то обе точки внутри полукруга, и при дальнейшем увеличении радиуса интеграл уже не изменится. При этом из теории известно, что при увеличении радиуса, доля результата, приходящегося на горизонтальный отрезок, растёт, а по дуге - стремится к 0, потому что здесь степень знаменателя на 4 больше, чем числителя, то есть модуль функции величина порядка 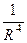 , а дуга длины
, а дуга длины 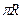 . Поэтому интеграл по дуге меньше, чем
. Поэтому интеграл по дуге меньше, чем 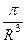 , и стремится к 0. В пределе, действительная ось - граница верхней полуплоскости.
, и стремится к 0. В пределе, действительная ось - граница верхней полуплоскости.
 =
= 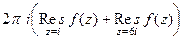 , где
, где  .
.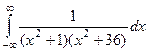 =
=  =
=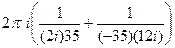 =
= 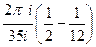 =
= 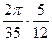 =
= 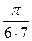 =
= 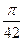 .
.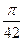 .
.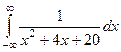 .
.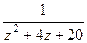 .
.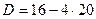 =
=  . Тогда
. Тогда  =
= 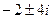 .
.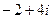 .
.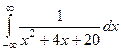 =
=  =
=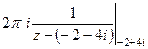 =
= 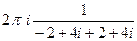 =
=  =
= 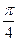 .
.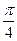 .
.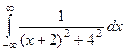 =
=  =
= 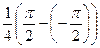 =
=  .
. .
.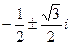 . Ответ.
. Ответ.  .
. .
.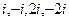 . Из них в верхней полуплоскости
. Из них в верхней полуплоскости 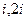 .
.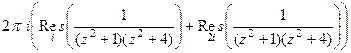 =
=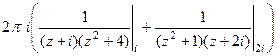 =
= 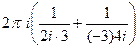 =
=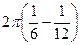 =
= 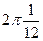 =
= 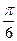 .
. 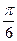 .
.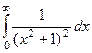 .
.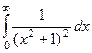 =
=  . Для функции
. Для функции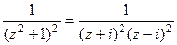 в верхней полуплоскости единственная особая точка, это
в верхней полуплоскости единственная особая точка, это 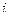 , полюс 2-го порядка.
, полюс 2-го порядка. 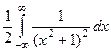 =
= 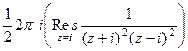 =
=  =
=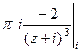 =
= 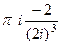 =
= 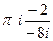 =
=  . Ответ.
. Ответ. 


