
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства векторного произведения: (алгебраические)
3) [λa, b ] = Л [ a, b ]. Геометрически свойства векторного произведения: 1)модуль вектороного произведения чесленно равен площади параллелограмма, построенного на векторах a и b; 2) векторное произведение = нулевому вектору, тогда и только тогда, когда множители коллинеарны(если они лежат на параллельных прямых или на одной прямой). Представление в виде определителя:
Если система координат левая, то их векторное произведение имеет вид: Результирующий вектор - средний вектор, т. е. векторная сумма составляющих векторов. Вычисляется за некоторый период времени.
Общее определение линейного пространства. Линейное векторное пространство. Примеры линейных пространств.
Умножение: λ*U, U Аксиомы (свойства) линейного пространства: 1) 2) 3) существует такой элемент 4) для любого 5) 6) 7) 8) Пример линейного пространства: Гильбертово пространство - пространство последовательностей со сходящимся рядом квадратов. Элементами (векторами) такого пространства являются бесконечные числовые последовательности x = (x1, x2,..., xn,...) такие, что ряд x21+ x22+... + х2n+... сходится. 24. n-мерное линейное векторное пространство. Размерность и базис векторного пространства. Разложение вектора по системе векторов. Переход к новому базису. n -мерное векторное пространство – пространство, имеющее n измерений (размерности n). Обычно этот термин применяется к пространству размерностью более трёх. При n=∞ имеем бесконечномерное пространство.
Размерность векторного пространства -максимальное число линейно-независимых векторов в векторном (линейном) пространстве. Если это число конечно, то пространство называется конечномерным (многомерным). В противном случае — бесконечномерным. Базис векторного пространства - набор из максимального (для данногопространства) числа линейно независимых векторов. Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты). Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑ aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n -мерный вектор — это упорядоченная совокупность n чисел {ai}. Размерность векторного пространства равна количеству векторов, составляющих его базис.
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.15.94 (0.007 с.) |

 1)
1) 

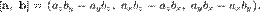
 Линейным (векторным) пространством называется множество Vпроизвольных элементов, названных векторами, в котором определены операции сложения и умножения вектора на число.
Линейным (векторным) пространством называется множество Vпроизвольных элементов, названных векторами, в котором определены операции сложения и умножения вектора на число. Сумма:U + V, U, V
Сумма:U + V, U, V  Vлинейные операции
Vлинейные операции , для любых
, для любых  (коммутативность сложения);
(коммутативность сложения);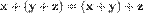 , для любых
, для любых  (ассоциативность сложения);
(ассоциативность сложения); , что
, что  для любого
для любого 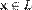 (существование нейтрального элемента относительно сложения), в частности L не пусто;
(существование нейтрального элемента относительно сложения), в частности L не пусто; существует такой элемент
существует такой элемент  , что
, что  (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения). (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр); (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор). (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров); (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).


