
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы лин. Ур-ий. Реш-ие сист. Лин. Ур-ий. Теорема кронекера-капелли.
Теорема Кронекера-Капелли: СЛАУ совместна (имеет одно решение), тогда и только тогда, когда ранг расширенной матрицы равен рангу основной. Теоремы: 1.Если ранг совместной сисемы равен числу неизвестных, т.е. r=n, то системы имеет единственное решение. 2. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Решение систем лин. ур-ий: 1. Найти ранг основной и расширенной матрицы системы. Если ранг основной матрицы отличен от ранга расширенной, то согласно теории Кронекера- Капелли, матрица несовместная, нет решений. 2. если ранг основной матрицы равен рангу расширенной, то система совместна:1) найти какой-либо базисный минор порядка (тот минор, который определяет ранг); 2)Взять r-уравнений, из коэффициентов которых составлен базисный минор. Неизвестные коэффициенты которых входят в базисный минор называются главными и остаются слева, а остальные n-r неизвестных называют свободными и переносят в правую часть ур-ий. 3. Найти выражение главных неизвестных через свободные, получено общее решение. 4.Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений. 14. Решение невырожденных систем линейных ур-ий. Теорема Крамера. Привести пример решения СЛАУ методом Крамера. Если определитель системы отличен от нуля, то система называется невырожденной. Метод Крамера: Этот метод применятся для решения систем линейных уравнений, в которых число уравнений ТЕОРЕМА (Крамера). Если в системе линейных уравнений число уравнений
где ПРИМЕР. Решить методом Крамера систему:
Так как число уравнений и число неизвестных в системе совпадают, и определитель матрицы системы
Следовательно, Если кол-во ур-ий не равно кол-ву неизвестных, то систему решать методом Гауса. 15. Решение систем лин. ур-ий методом обратной матрицы. Условие существования данного решения. Решение ур-ий вида АХ=В,ХА=В,АХВ=С. ОПРЕДЕЛЕНИЕ: Обратной к матрице СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ 1) Если матрица Действительно, чтобы существовали произведения 2) Если обратная матрица существует, то она единственная. Действительно, если предположить, что существует две матрицы
то будет существовать и произведение
и Следовательно, 3) Если матрица
Действительно, так как
и, следовательно, Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. Условие невырожденности матрицы Условие существования решения методом обратной матрицы.: Матрица где
Матрица Решение ур-ий вида АХ = В, ХА = В, АХВ = С АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица.
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.21.5 (0.009 с.) |
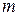 и число неизвестных
и число неизвестных 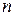 совпадают и матрица
совпадают и матрица 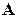 системы – невырожденная. Справедлива следующая теорема.
системы – невырожденная. Справедлива следующая теорема.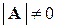 , то система совместна и имеет единственное решение, которое может быть найдено по формулам
, то система совместна и имеет единственное решение, которое может быть найдено по формулам 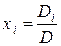 (
(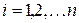 ) - формулы Крамера
) - формулы Крамера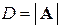 , а
, а 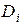 – определитель, получаемый из определителя
– определитель, получаемый из определителя 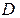 заменой его
заменой его 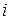 -го столбца на столбец свободных членов.
-го столбца на столбец свободных членов.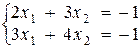
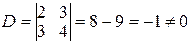 , то решение системы может быть найдено по формулам Крамера. Имеем:
, то решение системы может быть найдено по формулам Крамера. Имеем: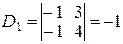 ,
, 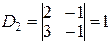 .
.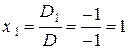 ,
, 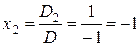 .
.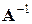 , такая, что
, такая, что 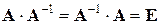 .
.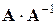 и
и 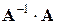 необходимо, чтобы матрицы
необходимо, чтобы матрицы 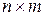 и
и 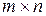 . Тогда матрица
. Тогда матрица 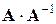 будет иметь размер
будет иметь размер 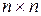 , а матрица
, а матрица 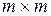 . Но для равенства
. Но для равенства 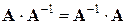 необходимо, чтобы размеры матриц
необходимо, чтобы размеры матриц 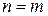 .
.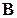 и
и 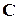 обладающие свойством
обладающие свойством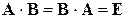 и
и 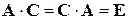 ,
,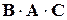 , причем
, причем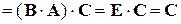
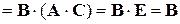 .
.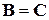 .
.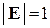 и для любых квадратных матриц
и для любых квадратных матриц 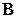
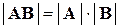 , то
, то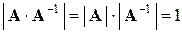
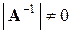 .
.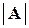 отличен от нуля. Причем обратная матрица
отличен от нуля. Причем обратная матрица 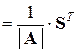 ,
,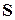 – матрица из алгебраических дополнений элементов матрицы
– матрица из алгебраических дополнений элементов матрицы 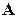 , т.е.
, т.е.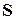
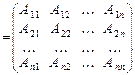 .
.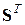 называется союзной (или присоединенной, или взаимной) для матрицы
называется союзной (или присоединенной, или взаимной) для матрицы 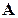 .
.


