
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 10. Ранг матрицы. Теорема о ранге матрицы.
Рангом матрицы А наз-ся наивысший порядок отличных от нуля миноров этой матрицы. Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А). Доказательство. Пусть того же числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы Билет 11. Понятие линейной зависимость и линейной независимости строк (столбцов) матрицы. Теорема о ранге матрицы. Столбец
где Если столбцы в (3.1) имеют вид то матричному равенству (3.1) соответствуют поэлементные равенства, Набор столбцов Система из
Здесь и далее символом о обозначается нулевой столбец соответствующих размеров. Система из Замечания 3.1 1. Один столбец 2. Любая часть системы столбцов называется подсистемой. Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А). Доказательство. Пусть
Системы линейных алгебраических уравнений (СЛАУ). Основные понятия. Матричная форма записи СЛАУ. Основные понятия: Ситемой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида
Решением системы 1 называется n- значением: x1=c1, x2=c2, xn=cn, где сij= const, при подстановке которых в один, все уравнения обращаются в верные равенства.
b= c2 cn Cистема называется совместной, если она имеет хотя бы одно решение; и несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение; и неопределенной, если она имеет более одного решения. Каждое решение будем называть частным решением. Совокупность частных решений образует общее решение. Решить систему означает выяснить, совместна она или нет. Если совместна, то найти общее решение. (aij), i = 1, m, называются коэффициентами j = 1, n системы bi- свободные члены,xi-неизвестное A x = B – матричная форма записи СЛАУ.
А=
Х=
b=
Две системы назыв. эквивалентными (равносильными), если они имеют одно и тоже общее решение,т.е. любое решение одной из них явл. Решением другой и наоборот. Замечание: Эквивалентные системы получаются в частности при элементарных преобразованиях системы и при условии, что преобразования совершаются лишь над строками матрицы. СЛАУ назыв. однородной, если все ее свободные члены равны нулю Замечание: однородная сист. Всегда совместна, поскольку существуют тривиальные решения: х1=о, х2=0, хm=0.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.86.155 (0.007 с.) |
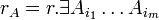 - столбцы, не входящие в БМ и они - максимальная линейно независимая система. Ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему)
- столбцы, не входящие в БМ и они - максимальная линейно независимая система. Ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему) 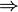 по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то
по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то 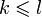 )
) 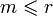 . по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и
. по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и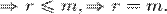
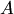 называется линейной комбинацией столбцов
называется линейной комбинацией столбцов 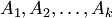 одинаковых размеров, если
одинаковых размеров, если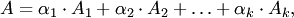 (3.1)
(3.1)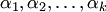 — некоторые числа. В этом случае говорят, что столбец
— некоторые числа. В этом случае говорят, что столбец 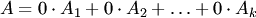 с нулевыми коэффициентами называется тривиальной.
с нулевыми коэффициентами называется тривиальной.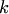 столбцов
столбцов 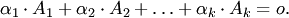 (3.2)
(3.2)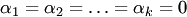 , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
, т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).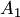 тоже образует систему: при
тоже образует систему: при  — линейно зависимую, а при
— линейно зависимую, а при 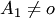 линейно независимую.
линейно независимую.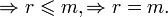
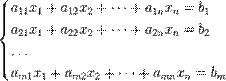
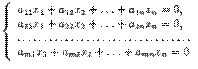 c1
c1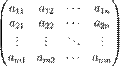
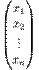
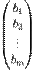 Ах=b
Ах=b Расширенной матрицей системы (А) называется матрица, получающаяся из исходной матрицы системы, присоединением вектора столбца свободных членов.
Расширенной матрицей системы (А) называется матрица, получающаяся из исходной матрицы системы, присоединением вектора столбца свободных членов.
 А= (А b)
А= (А b)


