
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение перемещений в упругих системах
2.1 Компоненты перемещения сечения в плоских стержневых системах В плоских стержневых системах обычно определяют два вида перемещений: изменения координат центров тяжести сечений, называемые линейными перемещениями, и углы поворота плоских сечений, называемые угловыми перемещениями. Зная эти компоненты, можно всегда определить положение любой точки системы после деформации В строительной механике любые компоненты перемещения принято обозначать буквой дельта с двумя индексами
2.2. Действительные и возможные перемещения. Действительная и возможная работа внешних сил Условие малости перемещений приводит к условию, что внешние силы не меняют своего направления в процессе деформации системы. В дальнейшем будем рассматривать системы, подчиняющиеся закону Гука. Это значит, что если где k - коэффициент пропорциональности. На схеме, Для конкретной силы Р различают действительное и возможное перемещение. Под действительным будем понимать перемещение
Подсчитаем работу силы При этом сила Промежуточное значение силы обозначим Здесь Перемещение прямо пропорционально силе, поэтому Подставив последнее выражение в (2.2), вычислим работу на всем пути нагружения, как Действительная работа внешней силы Вывод этой теоремы приведен в п. 2.7. Под возможным перемещением будем понимать любое малое перемещение, допускаемое имеющимися связями и независящее от заданной нагрузки. Чаще всего за возможные перемещения можно принять перемещения, вызванные другой системой нагрузок. Так перемещение
В формуле (2.5) отсутствует множитель 0,5, так как
2.3. Принцип возможных перемещений. Возможная работа внутренних сил Принцип возможных перемещений состоит в следующем [1]: если некоторая механическая система под действием заданных сил находится в равновесии, то работа сил, приложенных к этой системе, на любых бесконечно малых возможных перемещениях равна нулю. Этот принцип является необходимым и достаточным условием равновесия любой механической системы. Он следует из общего уравнения механики Даламбера-Лагранжа [2]. Доказано [1], что, применяя принцип возможных перемещений к упругим системам, вместо бесконечно малых возможных перемещений можно рассматривать малые, но конечные перемещения, которые возникают от конкретной нагрузки. Кроме того, можно возможные перемещения отсчитывать не от деформированного состояния, а от начального, ненагруженного. Выделим двумя сечениями бесконечно малые участки рамы в двух состояниях: в действительном и в состоянии, вызывающем возможные перемещения. В каждом из этих состояний в сечениях действуют внутренние силовые факторы M, N, Q. В дальнейшем не будем учитывать влияние поперечных сил Q, так как оно обычно мало по сравнению с влиянием M и N. Силовые факторы M и N в действительном состоянии 1 являются внутренними силовыми факторами для всей системы, но для выделенного бесконечно малого элемента они являются внешним моментом и внешней силой. Поэтому мы можем подсчитать элементарную возможную работу этих факторов, используя формулу (2.5), как работу внешних сил на возможных перемещениях, вызванных силами во втором состоянии Таким образом, Для вычисления элементарной работы Отсюда следует важный вывод что возможная работа внутренних сил (сил упругости) равна возможной работе внешних сил, но с обратным знаком. Подставляя (2.6) в (2.8), получим Просуммировав возможную работу внутренних сил по всей стержневой системе, будем иметь где интегрирование проводится по каждому стержню, а суммирование - по всем стержням, образующим систему. Если действительное состояние имеет индекс i, а возможное состояние j, то Формула (2.11) показывает, что за действительное можно принять любое из двух - тогда другое состояние будет считаться возможным для первого. 2.4 Формула Мора для определения перемещений Применяя принцип возможных перемещений для всей системы, запишем Отсюда получаем формулу для возможной работы внешних сил Вывод формулы для определения перемещения точки С по направлению i проведем на примере системы Причиной перемещения является равномерно распределенная нагрузка q. Обозначим состояние системы индексом q. Наряду с ним рассмотрим ту же систему, но при действии на нее силы
Обозначим это состояние индексом i. Примем состояние i за действительное, а состояние q за состояние, в котором перемещения будут возможными для сил в состоянии i. Воспользуемся (2.13) для подсчета возможной работы сил в состоянии i на возможных перемещениях в состоянии q Здесь учтено, что по длине стержней N - постоянная величина. Подставив Формула (2.14) называется формулой Мора - по фамилии ученого, впервые его получившего. В этой формуле значения внутренних силовых факторов в i -том состоянии обозначены черточками сверху. Это значит, что они возникают в сечениях системы от действия единичного силового фактора, приложенного по направлению искомого перемещения или его проекции. Величины 1. Построить эпюры внутренних силовых факторов от нагрузки, вызывающей перемещение (эп. 2. По направлению искомого перемещения приложить единичный силовой фактор (если определяется линейное перемещение, то прикладывается единичная сила, если определяется угол поворота сечения - то сосредоточенный момент) и построить эпюры внутренних силовых факторов (эп. 3. Перемножить соответствующие функции на каждом участке, вычислить интегралы и результаты просуммировать по всем стержням системы в соответствии с (2.14). Следует отметить, что обе суммы в формуле (2.14) При расчете ферм, ввиду отсутствия изгибающих моментов, для определения перемещений применяется формула где При расчете рам часто можно пренебречь осевой деформацией и учитывать только изгибную
2.4.1 Вычисление интегралов Мора. Правило Верещагина. Примеры Процедуру перемножения функций, например, изгибающих моментов в двух состояниях и последующего интегрирования произведения в пределах одного участка системы можно значительно упростить, если воспользоваться так называемым правилом Верещагина. Фрагменты эпюр моментов в двух состояниях: действительном, в котором действует заданная нагрузка, и единичном (воображаемом). В действительном состоянии эпюра моментов может иметь криволинейное очертание, а в единичном - всегда прямолинейное. Воспользуемся последним обстоятельством и продолжим прямую эпюры Здесь введено обозначение где Окончательно правило Верещагина формулируется следующим образом: для того, чтобы вычислить интеграл от произведения двух эпюр, нужно площадь криволинейной эпюры умножить на ординату прямолинейной под центром тяжести криволинейной и результат разделить на EJ. Если обе эпюры прямолинейные, то площадь и центр тяжести можно вычислять у любой из них, а ординату - у другой. Обычно криволинейность эпюры а площадь параболического сегмента с центром тяжести посередине участка. Прямолинейную часть эпюры можно, в свою очередь, рассматривать как сумму двух треугольных эпюр с центрами тяжести в соответствующей трети участка. ПРИМЕР №1
Для заданной рамы определить линейные и угловые перемещения по направлению 1,2 и 3. Для вычисления всех перемещений нужно построить эпюру моментов от заданной нагрузки. Начнем с определения опорных реакций. Для определения реакции составим уравнение равновесия
Для определения вертикальной составляющей реакции в точке А составим уравнение равновесия
Для определения горизонтальной составляющей
Проверка Реакции найдены верно. Проводим разрез на ригеле и рассматриваем правую оставшуюся часть Составим уравнение равновесия
Получили положительный результат, значит - момент в сечении действует именно так, то есть вызывает растягивающие напряжения в нижних волокнах стержня. Следовательно, ординаты эпюры откладываем вниз - в сторону растянутых волокон. Эпюра имеет треугольный вид. Проведя разрез на левой части ригеля (консоли), убеждаемся, что там При построении эпюры
направленной в сторону действия нагрузки q При таком способе построения не определяется точка экстремума изгибающего момента, но для вычисления перемещения она не нужна. В нашем случае точка экстремума Для определения проекции перемещения точки С на направление 1, приложим по этому направлению единичную силу Применим формулу Мора в виде (2.16) Положительный результат означает, что проекция перемещения точки С на направление 1, при действии нагрузки q, направлена вниз. Определим линейное перемещение точки В по направлению 2. Для этого приложим в точке В единичную силу
Точка перемещается вправо (по направлению Для этого приложим в сечении А сосредоточенный момент
Сечение А поворачивается по часовой стрелке (по направлению
2.5. Матричный алгоритм определения перемещений 2.5.1. Эпюры внутренних усилий в матричной записи. Матрица влияния Рассмотрим раму и построим для нее эпюру изгибающих моментов. При этом наряду с эпюрой М будем рассматривать матрицу-столбец, элементы которой численно равны ординатам эпюры М в начале и конце участков, на которые предварительно разделим данную стержневую систему Сечения в начале и конце каждого участка отметим цифрами. Кроме того, для каждого участка введем правило знаков для ординат эпюры М, которые при построении были отложены от оси рамы в сторону растянутого волокна. На участках, где нет равномерно распределенной нагрузки, эпюра М очерчивается прямой линией, которая полностью определяется значениями ординат в начале и конце участка (соответствующими элементами матрицы-столбца). На участках, где действует равномерно распределенная нагрузка эпюра М очерчена по квадратной параболе и поэтому должна определяться тремя параметрами. Третьим параметром будет служить стрелка f, определение которой дано в примере п. 2.4.1. Фрагмент эпюры М на участке, где действует равномерно распределенная нагрузка и формула для стрелки f. Таким образом, структура матрицы-столбца эпюры М (чаще мы будем говорить вектора эпюры моментов Воспользуемся принципом независимости действия сил: будем строить эпюры моментов от каждого вида нагрузок равных 1 и записывать эти эпюры в виде векторов. Все три вектора составим вместе, образуя так называемую матрицу влияния моментов (2.21).
Образуем матрицу-столбец (вектор) нагрузки Вектор окончательной эпюры моментов (2.20) определяется по формуле
Построим эпюру М, откладывая ординаты, равные по величине элементам Матрицы влияния широко применяются в строительной механике. Рассмотрим структуру матриц влияния моментов в общем виде. Для этого элементы матрицы обозначим Применение формулы (2.22) целесообразно в случае, если одну и ту же систему нужно рассчитывать на разные сочетания нагрузок. При этом меняется только вектор нагрузки, а матрица во всех расчетах одна и та же. Например, построим эпюру М от другой системы нагрузок. При этом вектор нагрузки примет вид
Понятие матрицы влияния моментов приобретает глубокий смысл при построении линий влияния в балках. Проведем расчет в матричной форме. Разделим балку на 7 участков длиной d и пронумеруем сечения на границах участков. В отличие от схемы следующего и конец предыдущего участка отметим одним номером. Это можно сделать, если нагрузка не содержит сосредоточенных моментов, приводящих к скачкам в эпюре моментов. Далее выберем общее правило знаков для ординат М для всех участков балки. Будем последовательно устанавливать
|
|||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.072 с.) |
 ,где первый индекс указывает номер направления перемещения, а второй - номер или символ причины, вызывающей это перемещение. Индекс указывает на нагрузку, обозначенную символом Р, являющейся причиной рассматриваемой деформации. Линейные компоненты
,где первый индекс указывает номер направления перемещения, а второй - номер или символ причины, вызывающей это перемещение. Индекс указывает на нагрузку, обозначенную символом Р, являющейся причиной рассматриваемой деформации. Линейные компоненты  и
и  позволяют определить положение центра тяжести сечения после деформации, а угол поворот
позволяют определить положение центра тяжести сечения после деформации, а угол поворот  определяет положение сечения, на котором находится любая точка m. При этом считается, что продольные волокна при изгибе “друг на друга не давят“, то есть координата Y любой точки m в поперечном сечении остается неизменной. Следует отметить, что компоненты перемещения предполагаются малыми по сравнению с размерами сооружения. Это справедливо для большого класса строительных и механических конструкций. При взгляде, например, на городской мост в часы пик невозможно увидеть, что он деформирован - это можно обнаружить только с помощью специальных приборов. При проектировании больших мостов максимальная составляющая перемещения по вертикали не должна превышать одной тысячной пролета.
определяет положение сечения, на котором находится любая точка m. При этом считается, что продольные волокна при изгибе “друг на друга не давят“, то есть координата Y любой точки m в поперечном сечении остается неизменной. Следует отметить, что компоненты перемещения предполагаются малыми по сравнению с размерами сооружения. Это справедливо для большого класса строительных и механических конструкций. При взгляде, например, на городской мост в часы пик невозможно увидеть, что он деформирован - это можно обнаружить только с помощью специальных приборов. При проектировании больших мостов максимальная составляющая перемещения по вертикали не должна превышать одной тысячной пролета. вызвано действием силы
вызвано действием силы  , то
, то , (2.1)
, (2.1) ;
;  , где
, где  и
и  разные по величине коэффициенты пропорциональности.
разные по величине коэффициенты пропорциональности. , вызванное силой
, вызванное силой  . Например, на схеме для силы
. Например, на схеме для силы  действительным будет перемещение
действительным будет перемещение  .
. при деформации рамы. Точка приложения силы
при деформации рамы. Точка приложения силы  перемещается по направлению этой силы на величину действительного перемещения
перемещается по направлению этой силы на величину действительного перемещения 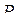 совершает работу, которую мы назовем действительной и обозначим
совершает работу, которую мы назовем действительной и обозначим 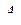 . При этом будем предполагать так называемое статическое приложение нагрузки, то есть постепенное медленное увеличение нагрузки от 0 до
. При этом будем предполагать так называемое статическое приложение нагрузки, то есть постепенное медленное увеличение нагрузки от 0 до 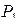 (настолько медленное, что ускорениями точек можно пренебречь).
(настолько медленное, что ускорениями точек можно пренебречь). , а соответствующее ей перемещение
, а соответствующее ей перемещение 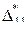 . В процессе увеличения сила
. В процессе увеличения сила 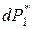 . Подсчитаем элементарную работу силы
. Подсчитаем элементарную работу силы  на соответствующем приращении перемещения
на соответствующем приращении перемещения 

 . (2.2)
. (2.2)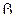 - некоторый коэффициент, учитывающий переменность
- некоторый коэффициент, учитывающий переменность 
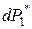 на интервале приращения перемещения. При этом мы пренебрегаем слагаемым
на интервале приращения перемещения. При этом мы пренебрегаем слагаемым  , которое является бесконечно малой величиной высшего порядка.
, которое является бесконечно малой величиной высшего порядка. и
и  .
. . (2.3)
. (2.3) 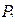 равна половине произведения величины силы на величину действительного перемещения по направлению силы (теорема Клайперона). В общем случае, при действии нескольких сил
равна половине произведения величины силы на величину действительного перемещения по направлению силы (теорема Клайперона). В общем случае, при действии нескольких сил  ,
,  ,...
,...  , согласно этой теореме, действительную работу внешних сил можно вычислить по формуле
, согласно этой теореме, действительную работу внешних сил можно вычислить по формуле  . (2.4)
. (2.4)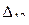 будет возможным для силы
будет возможным для силы  . При этом, если раме сообщить возможные перемещения, вызванные силой
. При этом, если раме сообщить возможные перемещения, вызванные силой  , то сила
, то сила  . (2.5)
. (2.5) =
=  +
+  .
.  внутренних сил в выделенном элементе, воспользуемся принципом возможных перемещений
внутренних сил в выделенном элементе, воспользуемся принципом возможных перемещений +
+  = 0. (2.7)
= 0. (2.7) =-
=- 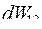 =
=  . (2.9)
. (2.9)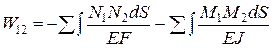 , (2.10)
, (2.10) . (2.11)
. (2.11)  . (2.12)
. (2.12)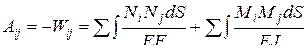 . (2.13)
. (2.13)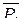 = 1 по направлению i
= 1 по направлению i
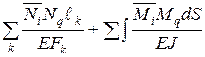 .
.  = 1, получим формулу для определения проекции полного перемещения на направление i
= 1, получим формулу для определения проекции полного перемещения на направление i
 и
и 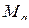 являются значениями внутренних силовых факторов в сечениях системы в состоянии q. Таким образом, для того, чтобы определить перемещение или проекцию его по какому-нибудь направлению по формуле Мора, нужно сделать следующее:
являются значениями внутренних силовых факторов в сечениях системы в состоянии q. Таким образом, для того, чтобы определить перемещение или проекцию его по какому-нибудь направлению по формуле Мора, нужно сделать следующее: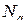 и эп.
и эп.  и эп.
и эп.  ).
).
 , (2.15)
, (2.15)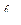 - длина конкретного стержня в ферме, а
- длина конкретного стержня в ферме, а  - площадь его поперечного сечения.
- площадь его поперечного сечения.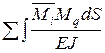 . (2.16)
. (2.16) . Обозначим расстояние от точки
. Обозначим расстояние от точки  до текущей ординаты
до текущей ординаты  через z. Тогда
через z. Тогда 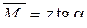 . Приступим к вычислению определенного интеграла, считая поперечное сечение стержня в пределах одного участка постоянным.
. Приступим к вычислению определенного интеграла, считая поперечное сечение стержня в пределах одного участка постоянным. =
=  .
. - элементарная площадь эпюры
- элементарная площадь эпюры  ) относительно оси y. Там же доказывается, что если известна координата центра тяжести фигуры, то статический момент численно равен произведению площади на эту координату. Таким образом, обозначив
) относительно оси y. Там же доказывается, что если известна координата центра тяжести фигуры, то статический момент численно равен произведению площади на эту координату. Таким образом, обозначив  - координату центра тяжести эпюры
- координату центра тяжести эпюры  - площадь эпюры
- площадь эпюры 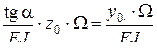 , (2.17)
, (2.17) - ордината эпюры
- ордината эпюры  и
и  , называют стрелкой и обозначают f. От действия равномерно распределенной нагрузки q всегда
, называют стрелкой и обозначают f. От действия равномерно распределенной нагрузки q всегда  , (2.18)
, (2.18) (2.19)
(2.19) ;
; ;
;  .
. ;
; ;
; 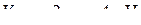 .
.
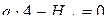 ;
; 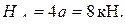


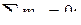

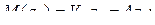
 =0.
=0.
 на стойке будет в верхнем сечении, где Q = 0.
на стойке будет в верхнем сечении, где Q = 0. и построим эпюру
и построим эпюру 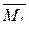 .
. =
=  (м).
(м). по этому направлению и построим эпюру
по этому направлению и построим эпюру 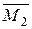 . Применим формулу Мора в виде (2.16) и способ Верещагина
. Применим формулу Мора в виде (2.16) и способ Верещагина м.
м.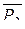 ). Определим угол поворота сечения А по направлению 3.
). Определим угол поворота сечения А по направлению 3. и построим эпюру
и построим эпюру  . Далее применим формулу Мора и правило Верещагина. В таких случаях говорят “перемножим эпюры
. Далее применим формулу Мора и правило Верещагина. В таких случаях говорят “перемножим эпюры  радиан.
радиан. ).
). ) имеет вид
) имеет вид (2.20)
(2.20)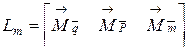 (2.21)
(2.21)
 .
. . (2.22)
. (2.22)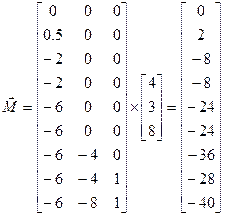
 перпендикулярно оси участка в соответствии с выбранным правилом знаков для этого участка.
перпендикулярно оси участка в соответствии с выбранным правилом знаков для этого участка. , где i - номер сечения, а j - индекс единичной нагрузки, вызывающей изгиб. Элементы строки с номером i представляют собой значения момента в сечении i от разных нагрузок, равных 1. При умножении этой строки на вектор нагрузки автоматически (в соответствии с правилом умножения матриц) происходит умножение значений ординат эпюр от единичных нагрузок (единичных эпюр) на действительное значение нагрузок и их сложение. Таким образом, формула (2.22) лаконично выражает целый процесс умножения единичных эпюр на каждую из нагрузок и их сложение.
, где i - номер сечения, а j - индекс единичной нагрузки, вызывающей изгиб. Элементы строки с номером i представляют собой значения момента в сечении i от разных нагрузок, равных 1. При умножении этой строки на вектор нагрузки автоматически (в соответствии с правилом умножения матриц) происходит умножение значений ординат эпюр от единичных нагрузок (единичных эпюр) на действительное значение нагрузок и их сложение. Таким образом, формула (2.22) лаконично выражает целый процесс умножения единичных эпюр на каждую из нагрузок и их сложение. применяя формулу (2.22), получим
применяя формулу (2.22), получим
 в узловые точки, записывать векторы моментов и составлять их рядом, образуя матрицу влияния моментов
в узловые точки, записывать векторы моментов и составлять их рядом, образуя матрицу влияния моментов .
.


