
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совместная обработка нескольких рядов (серий измерений)⇐ ПредыдущаяСтр 12 из 12
При выполнении бесконечных многократных наблюдений в течение длительного периода времени происходит изменение параметров средств измерений, изменение влияющих факторов, что неизбежно вызывает образование систематических и случайных изменений математических ожиданий и дисперсий, полученных в рядах. Для повышения точности измерений рекомендуется принимать меры в стабилизации параметров окружающей среды и каждый раз тщательно настраивать приборы. При выполнении таких измерений получают k – групп по n – результатов в каждом. Групповые средние арифметические значения и общие средние определяются по следующим формулам:
Оценка равнорассеянности групп наблюдений осуществляется путем расчета следующих оценок дисперсии и результатов: Общее рассеяние в ряде (группе) наблюдений: 1. где N – общее количество измерений. 2. Рассеяние между групповыми средними:
3. Рассеяние внутри каждой j – той группы:
4. Среднее рассеяние внутри групп:
Где j – номер ряда от 1…k; i – номер измерения в ряду от 1…nj; n – общее количество измерений в рядах. Для проверки гипотезы о равнорассеянности результатов используется F – распределение Фишера, которое описывает распределение отношений двух независимых оценок дисперсий. Если при выборной доверительной вероятности 0,95 В общем случае гипотезу о равнораспространенности групп результатов проверяют в два этапа: 1. Сначала проверяется гипотеза о равенстве дисперсий В противном случае необходимо проверить значимость отношений всех остальных дисперсий и необходимо считать дисперсии отличающиеся от существующих.
2. При равенстве дисперсий в группах проверяется гипотеза о равенстве математических ожиданий во всех группах. Если эта гипотеза верна, то оценки На практике для оценки гипотезы о равенстве средних арифметических используется распределение Стьюдента. Расчетная величина критерия определяется:
Если выполняется условие: (t1-2)<tT, то гипотеза о равенстве математических ожиданий принимается. Распределение Стьюдента используется для проверки значимости разности средних арифметических во всех группах, если проверка дисперсий в группах дала отрицательные результаты. Если выполненные расчеты показали, что оценки дисперсии и средних арифметических групп отличаются незначимо, то все результаты можно считать равнорассеянными, объединить их в один массив и обработать по методике многократных равноточных измерений. Значимое различие групповых средних арифметических свидетельствует о том,что на полученные результаты большое влияние оказали какие-то факторы, следует принять меры к их обнаружению и компенсации. Если значимыми являются различия дисперсии и незначимыми средних арифметических, то полученные результаты можно обрабатывать по методике неравноточных многократных измерений.
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.006 с.) |
 (8.8)
(8.8) ∙
∙  =
= 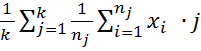 , где j=1…k; i=1…nj (8.9)
, где j=1…k; i=1…nj (8.9) ; (8.10)
; (8.10) . (8.11)
. (8.11) ; (8.12)
; (8.12) , (8.13)
, (8.13) , то различие оценок - возможные оценки дисперсии считается незначимым. В противном случае, расхождение дисперсии следует считать существенным и оно не может быть объяснено ограничением опытов данных.
, то различие оценок - возможные оценки дисперсии считается незначимым. В противном случае, расхождение дисперсии следует считать существенным и оно не может быть объяснено ограничением опытов данных. во всех группах наблюдений. Для этого их располагают в вариационный ряд в порядке возрастания
во всех группах наблюдений. Для этого их располагают в вариационный ряд в порядке возрастания  …
…  и проверяют значимость отношений дисперсий
и проверяют значимость отношений дисперсий  и
и  будут являться независимыми, точечными оценками одной и той же дисперсии, равной дисперсии результатов всех наблюдений. Отношения оценок подчиняются F – распределению Фишера и если расхождение этих оценок значимо, то с вероятностью следует считать, что при измерениях происходили случайные или систематические сдвиги математических ожиданий результатов и расхождения между средними арифметическими не определяются ограниченностью данных.
будут являться независимыми, точечными оценками одной и той же дисперсии, равной дисперсии результатов всех наблюдений. Отношения оценок подчиняются F – распределению Фишера и если расхождение этих оценок значимо, то с вероятностью следует считать, что при измерениях происходили случайные или систематические сдвиги математических ожиданий результатов и расхождения между средними арифметическими не определяются ограниченностью данных. ; (8.14)
; (8.14)


