
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные и интервальные оценки истинного
Значения измеряемой величины Точечные оценки. В метрологии для оценки параметров случайных величин на основе выборочных значений используют математическое ожидание и СКО. Оценки параметра называют точечными, если они выражаются одним числом. Любые точечные оценки выполняются на основании опытных данных. Они являются функциями случайных величин с распределенными, зависящими от распределения оцениваемых параметров измеряемой величины и числа опытов. По этим причинам точечные оценки должны удовлетворять требованиям состоятельности, несмещенности и эффективности. Используются несколько методов определения оценок, но наиболее распространен метод наибольшего правдоподобия. При выполнении многократных измерений истинное значение величины сосредоточено в наблюдении. Х1...Хn их можно рассматривать как n независимых случайных величин с одной функцией распространения Вероятность появления всех результатов может быть определена:
Суть этой методики состоит в том, что при изменении характеристик распространения В соответствии с методом Фишера, те значения, при которых В соответствии с данной методикой доказано, что точечными оценкой результатов измерений распределенных по нормальному закону являются:
Таким образом, оценкой истинного значения величины является среднее арифметическое значение, а оценкой дисперсии является среднее из квадратов отклонений результатов наблюдений от среднего арифметического. Исходя из теории наибольшего правдоподобия, для нормального закона распределения установлены следующие виды оценок: 1. Оценкой истинного значения является среднее арифметическое значение результатов отдельных измерений.
2. Оценка среднего квадратичного отклонения (СКО) результатов наблюдения
3. Оценка СКО среднего арифметического значения
4. Оценка СКО оценки среднего квадратического отклонения результатов наблюдений.
. (7.16)
Интервальные оценки Сущность оценки параметров измерений с помощью интервалов заключается в нахождении доверительных интервалов, между границами которых с какой-то доверительной вероятностью может находиться истинное значение оцениваемых параметров. Интервальные оценки применяются в сочетании с точечными. Допустим, при обработке результатов изменений получена точечная оценка, отвечающая требованиям состоятельности, несмещенности и эффективности:
Эта оценка используется вместо истинного значения Хист. = Q.
Xист
доверительный интервал
Рисунок 7.8 – Схема доверительного интервала Истинное значение величины будет с доверительной вероятностью находиться между границами доверительного интервала + ε:
Указанная вероятность может быть представлена в следующем виде
Ф – функция Лапласа. Величина
Половина доверительного интервала может быть представлена:
Формула доверительного интервала с учетом изложенного может быть представлена в следующем виде:
Поскольку на практике можно воспользоваться статистическими определенными видами оценок данная формула приводится к следующему виду:
где Для точного определения доверительного интервала для случайных величин Х, распространенных по нормальному закону при неизвестной дисперсии рекомендуется применять закон распространения Стьюдента с(n-1) степенями свободы. В этом случае
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.35 (0.007 с.) |
 , но вероятность Pi получения результата хi будет равна какой-то части общей вероятности.
, но вероятность Pi получения результата хi будет равна какой-то части общей вероятности. (7.11)
(7.11)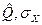 может быть достигнута наибольшая вероятность получения экспериментальных данных.
может быть достигнута наибольшая вероятность получения экспериментальных данных. достигнет наибольшего значения и принимаются в качестве точечных оценок истинного значения.
достигнет наибольшего значения и принимаются в качестве точечных оценок истинного значения. ;
;  (7.12)
(7.12)

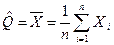 ; (7.13)
; (7.13)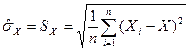 . (7.14)
. (7.14)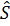 x
x 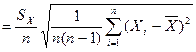 . (7.15)
. (7.15)
 . (7.17)
. (7.17) ε ε
ε ε





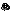
 0
0 Х
Х (7.18)
(7.18)

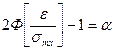 , (7.19)
, (7.19) - квантиль закона распределения,
- квантиль закона распределения, для различных законов распределения составляет следующие значения (Таблица 7.1 – Значения квантилей)
для различных законов распределения составляет следующие значения (Таблица 7.1 – Значения квантилей) вероятность, Р
закон распределения
вероятность, Р
закон распределения
 ; (7.20)
; (7.20) ; (7.21)
; (7.21)
 (7.22)
(7.22)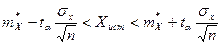 ; (7.23)
; (7.23) ; (7.24)
; (7.24)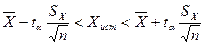 ; (7.25)
; (7.25)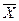 и SX – точечные оценки по результатам наблюдений
и SX – точечные оценки по результатам наблюдений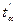 определяется по таблицам Стьюдента для соответствующей вероятности (Р = 0,90... 0,999):
определяется по таблицам Стьюдента для соответствующей вероятности (Р = 0,90... 0,999): (7.26) Распределения Стьюдента без всяких оснований закон распределения Стьюдента при определении
(7.26) Распределения Стьюдента без всяких оснований закон распределения Стьюдента при определении 


