
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Унитарные операторы и их свойства.
Определение. Линейный оператор U называется унитарным, если Утверждения. 1) Всякий унитарный оператор U в унитарном пространстве сохраняет скалярное произведение. Всякий линейный оператор U, сохраняющий скалярное произведение, унитарен. 2) Унитарный оператор не меняет длину векторов. 3) В ортонормированном базисе строки и столбцы матрицы унитарного оператора U ортонормированные. 4) Рассмотрим скалярное произведение Определение. Матрица с элементами Замечание. Т.к. переход от одного ортонормированного базиса к другому осуществляется унитарным оператором, матрица перехода от одного ортонормированного базиса к другому такому же является унитарной. Лемма 1. Собственные значение унитарного оператора по модулю равны 1 (лежат на окружности единичного радиуса). Доказательство. Пусть х – собственный вектор унитарного оператора U и
Лемма 2. Пусть унитарный оператор U, действующий в n-мерном пространстве Х, а е – его собственный вектор. Тогда (n-1)-мерное пространство Доказательство. Теорема 1. Для любого унитарного оператора в n-мерном пространстве существует n попарно ортогональных собственных векторов, соответствующие им собственные значения по модулю равны 1. Доказательство. Унитарный оператор U имеет в Х хотя бы один собственный вектор, обозначим его через
Теорема 2. Для любого унитарного оператора U в n-мерном пространстве Х существует ортонормированный базис, в котором матрица этого оператора диагональна: Доказательство. Пусть U – унитарный оператор, тогда по теореме 1 существует ортонормированный базис пространства Х из собственных векторов унитарного оператора U: 15. Спектральная характеристика нормального оператора. Критерий простоты структуры линейного оператора. Определение. Линейный оператор Замечание. Унитарные и самосопряженный линейные операторы являются частными случаями нормальных операторов. Теорема. Спектральная характеристика нормального оператора. Для того, чтобы существовал ортонормированный базис, в котором линейный оператор приводится к диагональной форме, необходимо и достаточно, чтобы Доказательство. Необходимость. Пусть в некотором ортонормированном базисе матрица оператора А диагональна Достаточность. Пусть
Пусть Определение. Теорема. Критерий простоты структуры линейного оператора. Для того, чтобы линейный оператор А имел простую структуру необходимо и достаточно, чтобы для любого корня Доказательство. Необходимость. А – оператор простой структуры. Следовательно, существуют n линейно независимых векторов, выбирая которые в качестве базиса L, получим, что матрица линейного оператора в базисе
Достаточность. Пусть
16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство. Теорема. Достаточный признак оператора простой структуры. Если все корни характеристического уравнения различны, то линейный оператор А имеет простую структуру. Доказательство. Пусть Теорема 1. У всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство. Доказательство. Выберем в линейном пространстве Х базис
Тогда ненулевое решение (1) существует, если 1)
|
||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.61.142 (0.01 с.) |
 .
. .
. 
 в Х и построим линейный оператор U в этом базисе:
в Х и построим линейный оператор U в этом базисе:  (1).
(1).  (2).
(2).  (3). Условие
(3). Условие  эквивалентно ортонормированности строк матрицы унитарного оператора. Условие
эквивалентно ортонормированности строк матрицы унитарного оператора. Условие  (4) эквивалентно ортонормированности строк матрицы унитарного оператора.
(4) эквивалентно ортонормированности строк матрицы унитарного оператора. . Следовательно, для того, чтобы линейный оператор U был унитарным необходимо и достаточно, чтобы он переводил какой-либо ортонормированный базим
. Следовательно, для того, чтобы линейный оператор U был унитарным необходимо и достаточно, чтобы он переводил какой-либо ортонормированный базим  .
.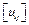 , удовлетворяющая условиям (3, 4), называется унитарной матрицей.
, удовлетворяющая условиям (3, 4), называется унитарной матрицей. - соответствующее собственное значение:
- соответствующее собственное значение:  . Рассмотрим
. Рассмотрим
 , состоящее из векторов
, состоящее из векторов  инвариантно относительно U.
инвариантно относительно U. пространство
пространство  . По лемме 2 (n-1)-мерное подпространство
. По лемме 2 (n-1)-мерное подпространство  (5).
(5). . В этом базисе матрица U имеет вид (5), а числа
. В этом базисе матрица U имеет вид (5), а числа  в силу леммы 1.
в силу леммы 1. называется нормальным, если
называется нормальным, если 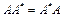 .
.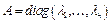 , т.к. базис ортонормированный, то матрица оператора
, т.к. базис ортонормированный, то матрица оператора  будет
будет  (транспонирование, сопряжение). Следовательно,
(транспонирование, сопряжение). Следовательно,  .
. Линейная оболочка
Линейная оболочка  будет одномерным инвариантным подпространством, а
будет одномерным инвариантным подпространством, а  будет также инвариантным подпространством. Докажем это:
будет также инвариантным подпространством. Докажем это: .
.  также будет принадлежать
также будет принадлежать  . Рассмотрим теперь действие оператора А из
. Рассмотрим теперь действие оператора А из  )… Продолжая этот процесс, получим ортогональный базис из собственных векторов, нормируем его – нормированный.
)… Продолжая этот процесс, получим ортогональный базис из собственных векторов, нормируем его – нормированный.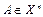 называется оператором простой структуры, если А имеет n линейно независимых собственных векторов.
называется оператором простой структуры, если А имеет n линейно независимых собственных векторов. характеристического уравнения кратности
характеристического уравнения кратности  ранг
ранг  .
. . Причем среди
. Причем среди  , то
, то  , где Р – матрица перехода от базиса е из собственных векторов к базису f. Следовательно
, где Р – матрица перехода от базиса е из собственных векторов к базису f. Следовательно  , т.е.
, т.е.  и
и  подобны и имеют одинаковый ранг.
подобны и имеют одинаковый ранг. 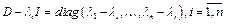 .
.  числу отличных от нуля ее диагональных элементов, т.е. числу корней характеристического уравнения неравных
числу отличных от нуля ее диагональных элементов, т.е. числу корней характеристического уравнения неравных  .
. - различные собственные значения оператора А. Собственные векторы, отвечающие собственному значению
- различные собственные значения оператора А. Собственные векторы, отвечающие собственному значению  . Следовательно, линейный оператор А имеет
. Следовательно, линейный оператор А имеет  собственных векторов
собственных векторов  . Покажем, что они линейно независимы в совокупности (от противного). Пусть это не так и равенство нулю линейной комбинации
. Покажем, что они линейно независимы в совокупности (от противного). Пусть это не так и равенство нулю линейной комбинации 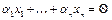 возможно при ненулевых коэффициентах. Следовательно, пусть
возможно при ненулевых коэффициентах. Следовательно, пусть  . Введем линейный оператор
. Введем линейный оператор 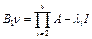 .
.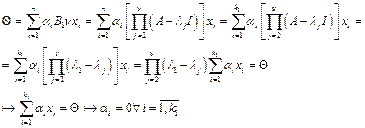
 . Покажем, что система
. Покажем, что система 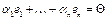 (1). Подействует линейным оператором
(1). Подействует линейным оператором  :
:  (2). Подействует на (2) линейным оператором
(2). Подействует на (2) линейным оператором  :
:  (3). Продолжая процесс вплоть до оператора
(3). Продолжая процесс вплоть до оператора  получим
получим 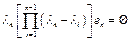 (4). Заметим, что (4) – это результат приложения оператора
(4). Заметим, что (4) – это результат приложения оператора  к исходному уравнению. Из (4) следует
к исходному уравнению. Из (4) следует  . Если к исходному уравнению применить оператор
. Если к исходному уравнению применить оператор  можно показать, что
можно показать, что  . И вообще соответствующим выбором оператора можно добиться, что все
. И вообще соответствующим выбором оператора можно добиться, что все  . Следовательно,
. Следовательно,  , преобразующая координаты
, преобразующая координаты  в координаты
в координаты  . Рассмотрим условие
. Рассмотрим условие  в координатной форме:
в координатной форме: (1)
(1)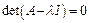 (2). И пусть
(2). И пусть  - корень уравнения (2). Возможны два случая:
- корень уравнения (2). Возможны два случая: решение системы (1), определяющее координаты собственного вектора х. х порождает одномерное инвариантное пространство;
решение системы (1), определяющее координаты собственного вектора х. х порождает одномерное инвариантное пространство; ). Пусть
). Пусть  - это решение системы (1). Подставим эти числа в (1) и отделим вещественную часть от мнимой.
- это решение системы (1). Подставим эти числа в (1) и отделим вещественную часть от мнимой.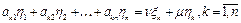 (3).
(3).  - координатами некоторого вектора х, а
- координатами некоторого вектора х, а  - координатами у, тогда
- координатами у, тогда 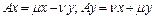 (4). Равенство (4) означает, что линейная оболочка
(4). Равенство (4) означает, что линейная оболочка  есть двумерное инвариантное подпространство относительное оператора.
есть двумерное инвариантное подпространство относительное оператора.


