
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратичные формы Приведение квадратичной формы к каноническому виду методом Лагранжа.Стр 1 из 11Следующая ⇒
Линейная алгебра. 1. Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Def: Линейная функция: В линейном пространстве L над полем R задана линейная функция (линейная форма), если каждому вектору х Î L поставлено в соответствие число f(x) так, что при этом выполняется следующее: 1) f(x+y)=f(x)+f(y); 2) f(λx)=λf(x) Def: А(x;y) называется билинейной формой от векторов x,y Î L(вещ.лин.пр-ва), если 1) При фиксированных y A(x;y) – есть линейная функция от х; a. A(x1+x2;y)=A(x1;y)+A(x2;y) b. A(λx;y)=λA(x;y) 2) При фиксированных х A(x;y) – есть линейная функция от у a. А(х;у1+у2)=А(х;у1)+А(х;у2) b. А(x;λy)=λA(x;y) Def: Линейная форма называется симметрической, если для все x,yÎL выполняется: A(x;y)=A(y;x) (Скалярное произведение в Евкл. Пространстве является примером симметрической формы). Выберем в линейном пространстве L базис e1,e2,…,en и выразим билинейную форму через координаты αi и βi векторов x,y соответственно в этом базисе. Тогда Преобразование матрицы билинейной формы при изменении базиса. Пусть в n-мерном пространстве даны 2 базиса e1,...,en и f1,...,fn и векторы f выражаются через векторы e с координатами сij. Тогда матрица С=[сij] (i,j=1..n) – матрица перехода от базиса e к базису f. С-невырожденная, С-1 – матрица перехода от f к e. Пусть А=[aik] – матрица билинейной формы в базисе е, а B=[bik] – матрица той же билинейной формы, но в базисе f. Найдем по матрице А матрицу В. Квадратичные формы Приведение квадратичной формы к каноническому виду методом Лагранжа. Def: Пусть А(х;у) – симметрическая билинейная форма. Функция А(х;х), которая получается их а(х;у) путем подстановки y=x называется квадратичной формой. При этом А(х;у) называется билинейной формой, полярной к А(х;х). Таким образом каждой симметрической билинейной форме соответствует одна квадратичная форма. Справедливо и обратное. При заданном базисе всякая квадратичная форма выражается формулой: Def: Квадратичная форма называется положительно определенной, если для x≠0 A(x;x)>0. Пусть А(х;х) – положительно определенная квадратичная форма, а А(х;у) ее полярная форма. Тогда: 1) А(х;у)=A(y;x) 2)A(x1+x2;y)=A(x1;y)+A(x2;y) 3)A(λx;y)=λA(x;y) 4)A(x;x)=0 ó x=0;
Критерий Сильвестра положительной определенности квадратичной формы. Определители Грамма. Критерий Сильвестра. Пусть А(х;у) – симметричная билинейная форма и f1,...,fn – базис n-мерного вещественного пространства L. Для того, чтобы квадратичная форма А(х;х) была положительно определена ó главные миноры были положительны. Доказательство: -> Пусть А(х;х) – положительно определенная квадратичная форма. Покажем, что главный минор Δk>0. Предположим, что Δk=0. Тогда одна из строк есть лиейная комбинация остальных. То есть их линейная комбинация может быть равна нулю при неравных нулю коэффициентах μi. Тогда (выписывая коэффициенты при μ) μ1A(f1;fi)+...+μkA(fk,fi)=0 для i=1..k. A(μ1f1+...μkfk;fi)=0 A(μ1f1+...μkfk; μ1f1+...μkfk)=0. Значит μ1f1+...μkfk=0. Противоречие, значит Δk ≠ 0 и А(x;x) можно привести к каноническому виду. Где <- Если Δ1>0,... то базис e1,...,en в котором квадратичная форма имеет канонический вид. Причем все λi >0/ Следовательно А(х;х)>0 для всех х. Т.е. Ах;х) – положительно определенная квадратичная форма. Определители Грамма. Выберем в качестве квадратичной формы скалярное произведение А(х;х)=(х,х). Пусть e1,...,en – векторы в пространстве E. Тогда Теорема. Определитель Грамма любой системы векторов всегда ≥0. Причем =0 ó e1,...,ek - линейно зависимы. Доказательство: Пусть e1,...,ek - линейно независимы. Рассмотрим А(х;у)=(х,у). Тогда определитель Грамма есть определитель матрицы B=[αij]=[A(ei;ej)]. ΔB = Δk. Т.к. А(х;х) – положительно определенная квадратичная форма, то из критерия Сильвестра: Δk>0. Если e1,...,ek – линейно зависимы, то одна из строк есть линейная комбинация всех остальных, значит определитель Грамма равен нулю. Определение. Пусть дан линейный оператор А:Х->Y, dimX=n. И некоторым базисом Х является e1,...,en. dimY=m; g1,...,gm – базис Y. x=α1e1+...+αnen. Ax= α1Ae1+...+αnAen. Другими словами, лиейный оператор полностью определяется совокупностью образов Aei базисных векторов е. y Î L(Ae1,...,Aen). Aej – вектор, содержащийся в Y и значит его можно разложить по базису Y. (*) Aej=a1jg1+...+anjgn. Коэффициенты aij определяют некоторую матрицу, в которой n строчек и n столбцов. Эту матрицу назовем матрицей А в базисах e1,...,en g1,...,gn. Столбцами матрицы оператора служат координаты векторов Ае1,...,Аеn в базисе g. Для того, чтобы определить элемент aij нужно найти образ Aej и взять его i-ую координату.
Утверждения. 1) Для того, чтобы линейный оператор А был эрмитовым необходимо и достаточно, чтобы соответствующая ему билинейная форма была эрмитовой: 2) Всякий линейный оператор А может быть записан в виде Замечание. Пусть А и В – самосопряженные линейные операторы. Для того, чтобы оператор АВ был самосопряженным необходимо и достаточно, чтобы АВ=ВА, т.е. чтобы линейные операторы А и В были перестановочными. Лемма 1. Собственные значения самосопряженного линейного оператора вещественные. Доказательство. Пусть х – собственный вектор линейного оператора А и
Лемма 2. Доказательство. Х, как ортогональное дополнение к Теорема 1. Для любого самосопряженного линейного оператора в n-мерном унитарном пространстве существует n попарно ортогональных собственных векторов, соответствующие им собственные значения вещественны. Доказательство. В Х существует хотя бы собственный вектор Теорема 2. А – самосопряженный линейный оператор в n-мерном унитарном пространстве, тогда существует ортогональный базис, в котором матрица линейного оператора А диагональна и вещественно. Верно и обратное. Доказательство. Необходимость. Выберем в качестве базиса построенные при доказательстве теоремы 1 собственные векторы Достаточность. Пусть матрица оператора А в ортонормированном базисе имеет вид (1). Итак, в ортонормированном базисе матрица Теорема 3. Собственные векторы самосопряженного оператора, соответствующие различным собственным значениям, взаимно ортогональны. Доказательство. Пусть у линейного оператора А имеются
Определение. Матрица Теорема 4. Для того, чтобы линейный оператор А был самосопряженным необходимо и достаточно, чтобы его матрица была эрмитовой. Теорема 5. Пусть в n-мерном унитарном пространстве Х задана эрмитова билинейная форма. Тогда в Х существует ортонормированный базис, в котором соответствующая билинейная квадратичная форма, записывается в виде:
Доказательство. Пусть
Утверждения. 1) Всякий унитарный оператор U в унитарном пространстве сохраняет скалярное произведение. Всякий линейный оператор U, сохраняющий скалярное произведение, унитарен. 2) Унитарный оператор не меняет длину векторов. 3) В ортонормированном базисе строки и столбцы матрицы унитарного оператора U ортонормированные. 4) Рассмотрим скалярное произведение Определение. Матрица с элементами Замечание. Т.к. переход от одного ортонормированного базиса к другому осуществляется унитарным оператором, матрица перехода от одного ортонормированного базиса к другому такому же является унитарной. Лемма 1. Собственные значение унитарного оператора по модулю равны 1 (лежат на окружности единичного радиуса). Доказательство. Пусть х – собственный вектор унитарного оператора U и
Лемма 2. Пусть унитарный оператор U, действующий в n-мерном пространстве Х, а е – его собственный вектор. Тогда (n-1)-мерное пространство Доказательство. Теорема 1. Для любого унитарного оператора в n-мерном пространстве существует n попарно ортогональных собственных векторов, соответствующие им собственные значения по модулю равны 1. Доказательство. Унитарный оператор U имеет в Х хотя бы один собственный вектор, обозначим его через
Теорема 2. Для любого унитарного оператора U в n-мерном пространстве Х существует ортонормированный базис, в котором матрица этого оператора диагональна: Доказательство. Пусть U – унитарный оператор, тогда по теореме 1 существует ортонормированный базис пространства Х из собственных векторов унитарного оператора U: 15. Спектральная характеристика нормального оператора. Критерий простоты структуры линейного оператора. Определение. Линейный оператор Замечание. Унитарные и самосопряженный линейные операторы являются частными случаями нормальных операторов. Теорема. Спектральная характеристика нормального оператора. Для того, чтобы существовал ортонормированный базис, в котором линейный оператор приводится к диагональной форме, необходимо и достаточно, чтобы Доказательство. Необходимость. Пусть в некотором ортонормированном базисе матрица оператора А диагональна Достаточность. Пусть
Пусть Определение. Теорема. Критерий простоты структуры линейного оператора. Для того, чтобы линейный оператор А имел простую структуру необходимо и достаточно, чтобы для любого корня Доказательство. Необходимость. А – оператор простой структуры. Следовательно, существуют n линейно независимых векторов, выбирая которые в качестве базиса L, получим, что матрица линейного оператора в базисе Достаточность. Пусть
16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство. Теорема. Достаточный признак оператора простой структуры. Если все корни характеристического уравнения различны, то линейный оператор А имеет простую структуру. Доказательство. Пусть Теорема 1. У всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство. Доказательство. Выберем в линейном пространстве Х базис
Тогда ненулевое решение (1) существует, если 1)
Свойства. 1) ортогональный оператор сохраняет длины векторов; 2) ортогональный оператор сохраняет углы между векторами. 3) Если 4) Матрица 5) Определитель матрицы ортонормированного оператора равен 6) Ортогональный оператор всегда не вырожден. 7) Тождественный оператор является ортогональным. 8) Произведение ортогональных операторов снова будет ортогональным оператором. 9) Оператор, обратный ортогональному, тоже ортогональный. 10) Линейный оператор, переводящий хотя бы один базис в ортонормированный, является ортогональным. Определение. Ортогональные операторы, определитель матрицы которых равен 1, называются собственными, у которых равен –1, несобственными. Лемма 3. Если Доказательство. Если взять Теорема 4. Матрица ортогонального оператора в некотором ортонормированном базисе имеет вид:
Доказательство. По теореме 1 (билет 16) любой линейный оператор в n-мерном евклидовом пространстве имеет одномерное или двумерное инвариантное подпространство
19. Определение аффинного пространства. Различные способы задания прямой в аффинном пространстве (векторный, в параметрическом виде, канонический, по двум точкам). Угол между прямыми. Нахождение расстояния от данной точки до данной прямой. Перпендикуляр, опущенный из точки на прямую. Def: пусть задано n-мерное векторное пространство Vn над полем F и непустое множество An, элементы которого будем называть точками. Предположим, что упорядоченной паре точек M,N Î An поставлен в соответствие вектор пространства Vn, обозначаемый 1)Для M Î An и a Î Vn единственная точка N Î An, что Тогда множество An называется n-мерным аффинным пространством, связанным с векторным пространством Vn. Способы задания прямой: Def: Будем называть прямой в аффинном пространстве множество точек этого пространства, получаемых из одной его точки всеми переносам, векторы которых коллинеарны. Т.к. векторы этих переносов имеют вид at, где t Î R, радиус-векторы прямой имеют вид (1) x=x0+at. 1) Уравнение 1 называется векторным уравнением прямой. При этом а – направляющий вектор. Две различные прямые, полученные из различных точек одними и теми же переносами, называются параллельными. 2) Координатные уравнения прямой. Уравнение 1 равносильно n координатным уравнениям (2) xi=x0+ait. Уравнение 2 – параметрическое уравнение прямой. Разрешая его относительно T и приравнивая полученные выражения получаем: 3) Уравнение прямой по двум точкам. Если задано две точки M0(x0) и M1(x1), то за направляющий вектор прямой, проходящей через эти две точки можно принять Расстояние от точки до прямой. Расстояние w от точки M(r) до произвольной точки прямой определяется соотношением (7): Перпендикуляр, опущенный из точки на прямую. Требуя, чтобы отрезок MN, соединяющий М(х) с некоторой точкой N прямой, был перпендикулярен направляющему вектору а этой прямой, т.е. чтобы вектор x-x0-at был ортогонален а. (x-x0-at,a)=0. Значение t, удовлетворяющее этому условию совпадает с 8. Это совпадение |-> основание N перпендикуляра, опущенного из данной точки М на прямую, совпадает с той точкой прямой, которая находится на минимальном расстоянии от данной точки. 20. Взаимное расположение двух прямых. Нахождение кратчайшего расстояния между двумя скрещивающимися прямыми. Общий перпендикуляр двух прямых. Взаимное расположение двух прямых. Если две прямые в n-мерном аффинном пространстве, определяющиеся уравнениями Кратчайшее расстояние между двумя скрещивающимися прямыми. Найдем кратчайшее расстояние между двумя скрещивающимися прямыми l и m, которые записаны уравнением (10):
Вектор MN имеет вид: Вычислим теперь 21. Различные способы задания плоскостей (векторный, в параметрическом виде, по точке и нормали, по точке и направляющим векторам, по n точкам). Основная теорема о плоскости. Угол между плоскостями. Условие принадлежности n+1 точки одной плоскости. Определение. Будем называть m-мерной плоскостью аффинного пространства или m-плоскостью множество всех точек этого пространства, полученных из одной его точки всеми переносами, векторы которых коллинеарны и принадлежат одному линейному пространству. Т.к. векторы этих переносов имеют вида Замечание. Прямые можно рассматривать, как 1-плоскость; точки – как 0-плоскость. Определение. Различные плоскости, получающиеся из различных точек одними и теми же переносами, называются параллельными плоскостями. ( Уравнение (1) равносильно Если задано m+1 точек Определение. Будем называть m-плоскость, определяемую точками Определение. Если m=n-1, то такая плоскость называется гиперплоскостью или просто плоскостью.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.190.147 (0.085 с.) |
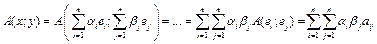 . Где aij=A(ei;ej). Тогда
. Где aij=A(ei;ej). Тогда 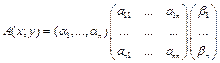 . Где матрица – матрица билинейной формы A(x;y) в базисе e1,...,en
. Где матрица – матрица билинейной формы A(x;y) в базисе e1,...,en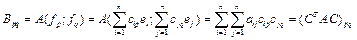 . То есть B=CTAC.
. То есть B=CTAC.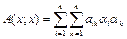 , где aik – значение билинейной формы A(ei;ek).
, где aik – значение билинейной формы A(ei;ek). . Отсюда, λ1>0(Δ1>0), λ2>0(Δ1>0,Δ2>0),...
. Отсюда, λ1>0(Δ1>0), λ2>0(Δ1>0,Δ2>0),... - определитель Грамма.
- определитель Грамма.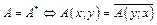 .
. ;
;
 .
.
 - его собственное значение:
- его собственное значение:
 – самосопряженный линейный оператор, а е – его собственный вектор. Тогда совокупность
– самосопряженный линейный оператор, а е – его собственный вектор. Тогда совокупность  есть (n-1)-мерное подпространство, инвариантное относительно линейного оператора А.
есть (n-1)-мерное подпространство, инвариантное относительно линейного оператора А. есть (n-1)-мерное подпространство в Х. Покажем, что это подпространство инвариантно относительно оператора А:
есть (n-1)-мерное подпространство в Х. Покажем, что это подпространство инвариантно относительно оператора А: 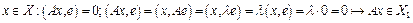 .
. линейного оператора А. По лемме 2 совокупность векторов ортогональных
линейного оператора А. По лемме 2 совокупность векторов ортогональных  . Будем рассматривать линейный оператор
. Будем рассматривать линейный оператор  . Продолжая этот процесс, мы получим в результате n попарно ортогональных собственных векторов
. Продолжая этот процесс, мы получим в результате n попарно ортогональных собственных векторов  . Согласно лемме 1, соответствующие собственные значения вещественны.
. Согласно лемме 1, соответствующие собственные значения вещественны. и пронормируем их. В этом базисе матрица оператора имеет вид:
и пронормируем их. В этом базисе матрица оператора имеет вид:  (1).
(1). получается из матрицы линейного оператора А транспонированием и заменой каждого элемента комплексным сопряжением. Проделав эти операции над матрицей вида (1), где все
получается из матрицы линейного оператора А транспонированием и заменой каждого элемента комплексным сопряжением. Проделав эти операции над матрицей вида (1), где все  - вещественные, мы получим ту же матрицу, следовательно А и
- вещественные, мы получим ту же матрицу, следовательно А и  .
.

 называется эрмитовой, если
называется эрмитовой, если  .
. - координаты Х.
- координаты Х. - эрмитова билинейная форма, т.е.
- эрмитова билинейная форма, т.е.  . Тогда существует самосопряженный линейный оператор А такой, что
. Тогда существует самосопряженный линейный оператор А такой, что  . Выберем в качестве базиса Х ортонормированную систему собственных векторов самосопряженного линейного оператора А (по теореме 1). Тогда
. Выберем в качестве базиса Х ортонормированную систему собственных векторов самосопряженного линейного оператора А (по теореме 1). Тогда  .
. .
. .
. 
 (1).
(1).  (2).
(2).  (3). Условие
(3). Условие  эквивалентно ортонормированности строк матрицы унитарного оператора. Условие
эквивалентно ортонормированности строк матрицы унитарного оператора. Условие  (4) эквивалентно ортонормированности строк матрицы унитарного оператора.
(4) эквивалентно ортонормированности строк матрицы унитарного оператора. . Следовательно, для того, чтобы линейный оператор U был унитарным необходимо и достаточно, чтобы он переводил какой-либо ортонормированный базим
. Следовательно, для того, чтобы линейный оператор U был унитарным необходимо и достаточно, чтобы он переводил какой-либо ортонормированный базим  .
.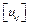 , удовлетворяющая условиям (3, 4), называется унитарной матрицей.
, удовлетворяющая условиям (3, 4), называется унитарной матрицей. . Рассмотрим
. Рассмотрим
 пространство
пространство  (5).
(5). . В этом базисе матрица U имеет вид (5), а числа
. В этом базисе матрица U имеет вид (5), а числа  в силу леммы 1.
в силу леммы 1.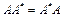 .
.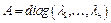 , т.к. базис ортонормированный, то матрица оператора
, т.к. базис ортонормированный, то матрица оператора  (транспонирование, сопряжение). Следовательно,
(транспонирование, сопряжение). Следовательно,  .
. Линейная оболочка
Линейная оболочка  будет одномерным инвариантным подпространством, а
будет одномерным инвариантным подпространством, а  будет также инвариантным подпространством. Докажем это:
будет также инвариантным подпространством. Докажем это: .
.  . Рассмотрим теперь действие оператора А из
. Рассмотрим теперь действие оператора А из  )… Продолжая этот процесс, получим ортогональный базис из собственных векторов, нормируем его – нормированный.
)… Продолжая этот процесс, получим ортогональный базис из собственных векторов, нормируем его – нормированный.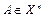 называется оператором простой структуры, если А имеет n линейно независимых собственных векторов.
называется оператором простой структуры, если А имеет n линейно независимых собственных векторов. ранг
ранг  .
. . Причем среди
. Причем среди  , то
, то  , где Р – матрица перехода от базиса е из собственных векторов к базису f. Следовательно
, где Р – матрица перехода от базиса е из собственных векторов к базису f. Следовательно  , т.е.
, т.е.  и
и  подобны и имеют одинаковый ранг.
подобны и имеют одинаковый ранг. 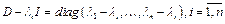 .
.  числу отличных от нуля ее диагональных элементов, т.е. числу корней характеристического уравнения неравных
числу отличных от нуля ее диагональных элементов, т.е. числу корней характеристического уравнения неравных  .
. - различные собственные значения оператора А. Собственные векторы, отвечающие собственному значению
- различные собственные значения оператора А. Собственные векторы, отвечающие собственному значению  . Следовательно, линейный оператор А имеет
. Следовательно, линейный оператор А имеет  собственных векторов
собственных векторов  . Покажем, что они линейно независимы в совокупности (от противного). Пусть это не так и равенство нулю линейной комбинации
. Покажем, что они линейно независимы в совокупности (от противного). Пусть это не так и равенство нулю линейной комбинации 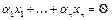 возможно при ненулевых коэффициентах. Следовательно, пусть
возможно при ненулевых коэффициентах. Следовательно, пусть  . Введем линейный оператор
. Введем линейный оператор 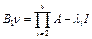 .
.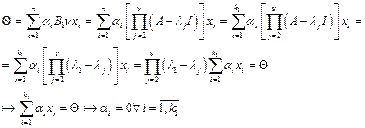
 . Покажем, что система
. Покажем, что система 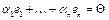 (1). Подействует линейным оператором
(1). Подействует линейным оператором  :
:  (2). Подействует на (2) линейным оператором
(2). Подействует на (2) линейным оператором  :
:  (3). Продолжая процесс вплоть до оператора
(3). Продолжая процесс вплоть до оператора  получим
получим 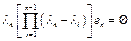 (4). Заметим, что (4) – это результат приложения оператора
(4). Заметим, что (4) – это результат приложения оператора  к исходному уравнению. Из (4) следует
к исходному уравнению. Из (4) следует  . Если к исходному уравнению применить оператор
. Если к исходному уравнению применить оператор  можно показать, что
можно показать, что  . И вообще соответствующим выбором оператора можно добиться, что все
. И вообще соответствующим выбором оператора можно добиться, что все  . Следовательно,
. Следовательно,  , преобразующая координаты
, преобразующая координаты  в координаты
в координаты  . Рассмотрим условие
. Рассмотрим условие  в координатной форме:
в координатной форме: (1)
(1)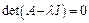 (2). И пусть
(2). И пусть  - корень уравнения (2). Возможны два случая:
- корень уравнения (2). Возможны два случая: решение системы (1), определяющее координаты собственного вектора х. х порождает одномерное инвариантное пространство;
решение системы (1), определяющее координаты собственного вектора х. х порождает одномерное инвариантное пространство; ). Пусть
). Пусть  - это решение системы (1). Подставим эти числа в (1) и отделим вещественную часть от мнимой.
- это решение системы (1). Подставим эти числа в (1) и отделим вещественную часть от мнимой.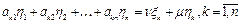 (3).
(3).  - координатами некоторого вектора х, а
- координатами некоторого вектора х, а  - координатами у, тогда
- координатами у, тогда 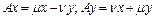 (4). Равенство (4) означает, что линейная оболочка
(4). Равенство (4) означает, что линейная оболочка  есть двумерное инвариантное подпространство относительное оператора.
есть двумерное инвариантное подпространство относительное оператора.
 тоже образуют ортонормированный базис в Х.
тоже образуют ортонормированный базис в Х.
 .
. .
.
 .
.
 также является инвариантным пространством.
также является инвариантным пространством. . Поскольку А – ортогональный оператор, он не вырожден и его образ на любом инвариантном подпространстве совпадает с этим пространством, поэтому х имеет свой прообраз
. Поскольку А – ортогональный оператор, он не вырожден и его образ на любом инвариантном подпространстве совпадает с этим пространством, поэтому х имеет свой прообраз  .
.
 . Если же
. Если же  . По лемме 3, ортогональное дополнение
. По лемме 3, ортогональное дополнение  соответствуют двумерным инвариантным пространствам.
соответствуют двумерным инвариантным пространствам.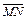 , причем выполнены следующие аксиомы:
, причем выполнены следующие аксиомы: .
. - каноническое уравнение прямой.
- каноническое уравнение прямой. =x1-x0 . Поэтому векторное уравнение этой прямой может быть записано в виде x=x0+(x1-x0)t, а каноническое уравнение:
=x1-x0 . Поэтому векторное уравнение этой прямой может быть записано в виде x=x0+(x1-x0)t, а каноническое уравнение: 
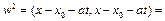

 . Исследуя w2 как функцию от t. (8)
. Исследуя w2 как функцию от t. (8)  - это значение даст минимальное расстояние. Подставляя 8 в 7 получаем:
- это значение даст минимальное расстояние. Подставляя 8 в 7 получаем: 
 (10) пересекаются (имеют одну общую точку), т.е. существуют такие значения t и u, когда
(10) пересекаются (имеют одну общую точку), т.е. существуют такие значения t и u, когда  . Т.е.
. Т.е.  линейно независимы. Если две прямые, заданные уравнения (10) параллельны и их направляющие векторы а, b коллинеарны, т.е.
линейно независимы. Если две прямые, заданные уравнения (10) параллельны и их направляющие векторы а, b коллинеарны, т.е.  . Т.о.
. Т.о. 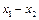 может быть представлен в виде линейной комбинации векторов а и b, т.е. в виде:
может быть представлен в виде линейной комбинации векторов а и b, т.е. в виде:  . Поэтому точка, радиус-вектором которой является этот вектор, есть точка пересечения данных прямых. Т.о. необходимым и достаточным условием того, что две прямые, заданные выражением (10), пересекаются или параллельны, является линейная зависимость тройки векторов
. Поэтому точка, радиус-вектором которой является этот вектор, есть точка пересечения данных прямых. Т.о. необходимым и достаточным условием того, что две прямые, заданные выражением (10), пересекаются или параллельны, является линейная зависимость тройки векторов  (13)
(13)


 :
: 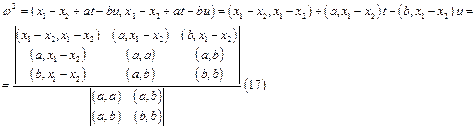 Общий перпендикуляр двух прямых. Требуем, чтобы отрезок, соединяющий произвольные точки двух данных прямых (10), был перпендикулярен направляющим векторам а и b обеих прямых. Мы получили условие (14), отсюда находим, что значение t и u, удовлетворяющие этому условию, совпадают со значением (15). Это совпадение показывает, что основания общего перпендикуляра двух прямых совпадают с теми точками эти прямых, расстояние между которыми минимально.
Общий перпендикуляр двух прямых. Требуем, чтобы отрезок, соединяющий произвольные точки двух данных прямых (10), был перпендикулярен направляющим векторам а и b обеих прямых. Мы получили условие (14), отсюда находим, что значение t и u, удовлетворяющие этому условию, совпадают со значением (15). Это совпадение показывает, что основания общего перпендикуляра двух прямых совпадают с теми точками эти прямых, расстояние между которыми минимально.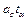 , где
, где 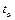 принимает все вещественные значения, то радиус-векторы точек m-плоскости имеют вид?
принимает все вещественные значения, то радиус-векторы точек m-плоскости имеют вид?  (1) – векторное уравнение m-плоскости. Векторы
(1) – векторное уравнение m-плоскости. Векторы 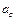 называются направляющими векторами m-плоскости.
называются направляющими векторами m-плоскости. ).
). (2) – параметрическое (координатное) уравнение m-плоскости в координатах.
(2) – параметрическое (координатное) уравнение m-плоскости в координатах. и векторы линейно независимы, то эти точки определяют единственную m-плоскость, проходящую через них. В этом случае за направляющие векторы этой плоскости можно принять векторы
и векторы линейно независимы, то эти точки определяют единственную m-плоскость, проходящую через них. В этом случае за направляющие векторы этой плоскости можно принять векторы  , и векторное уравнение m-плоскости может быть записано в виде:
, и векторное уравнение m-плоскости может быть записано в виде:  (3).
(3). - m-плоскостью
- m-плоскостью  .
.


