
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент корреляции двух случайных величин и его свойства
В практике для оценки тесноты статистической зависимости случайных величин более часто используется коэффициент корреляции, а не ковариация. Дело в том, что ковариация является размерной величиной, а коэффициент корреляции – безразмерной. Кроме того, коэффициент корреляции является универсальной мерой тесноты статистической зависимости, стандартизованной для различных случайных величин. Поэтому коэффициент корреляции позволяет сравнивать уровень связи случайных величин разной природы. Коэффициент корреляции равен:
или в другой записи:
Свойства коэффициента корреляции:
1. Абсолютная величина коэффициента корреляции не превышает 1: 2. Если коэффициент корреляции равен 1 или -1, то случайные величины 3. Если случайные величины
Законы больших чисел Законами больших чисел называются несколько теорем теории вероятностей, которые утверждают, что при неограниченном увеличении числа опытов или испытаний и при некоторых дополнительных условиях те или иные средние характеристики этих серий опытов стремятся к некоторым постоянным, т.е. имеют их в качестве пределов последовательностей средних характеристик соответствующих опытов. Эти теоремы отличаются друг от друга дополнительными условиями и теми средними величинами, о которых делаются утверждения этих теорем. При однократном проведении опыта никогда нельзя заранее определить его результат. Но теоремы больших чисел утверждают, что при достаточно большом числе повторений опытов те или иные средние значения случайных величин становятся близкими к некоторым константам. В каждой теореме больших чисел речь идёт о своих случайных величинах и их средних. Каждая теорема больших чисел определяет условия, при которых проявляются такие закономерности в стабилизации значений средних величин при большом числе опытов.
Сходимость по вероятности Последовательность случайных величин
То же утверждение можно записать с помощью использования понятия предела: для всякого Сходимость по вероятности
Так же, как и для обычного предела последовательности можно доказать, что если последовательность случайных величин имеет предел, то только один. Кроме того, можно доказать, что для любой непрерывной функции
Частным случаем сходимости последовательность Неравенства Чебышева Так называются следующие неравенства, которые верны для любой случайной величины
Эти неравенства иногда используются в другом виде, который получается, если заменить вероятности в них на вероятности противоположных событий, которые равны единице минус исходных вероятности:
Пример. Определим вероятность того, что произвольная случайная величина
Следовательно, значение вероятности отклонения для любой случайной величины Теорема Бернулли Формально схема Бернулли может быть описана следующим образом. Проводится последовательность из
Если обозначить через В схеме Бернулли возможно доказать одну из теорем больших чисел. Она утверждает следующее. Если Доказательство этой теоремы приведено в книге математике Якоба Бернулли «Искусство предположений», которая опубликована в 1713 году уже после его смерти. Поэтому теорема и была названа его именем. Значение этой теоремы, в частности, в том, что она обосновывает наблюдаемую в практике проведения разнообразных испытаний такую закономерность: при большом числе испытаний доля успехов неограниченно приближается к истинному значению вероятности отдельного успеха. Поэтому на практике можно определять вероятности в схеме Бернулли по статистическому определению, как частное от деления числа успехов на общее число проведённых испытаний. Это значение будет тем точнее, чем больше испытаний будет проведено. Доказательство теоремы Бернулли можно провести с использованием одного из неравенств Чебышева. Как известно, для случайной величины Следовательно, для случайной величины
Следовательно, в соответствии с последней формой неравенства Чебышева для случайной величины
Для любого
А это в свою очередь означает, что для всякого
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 3177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.156.46 (0.017 с.) |

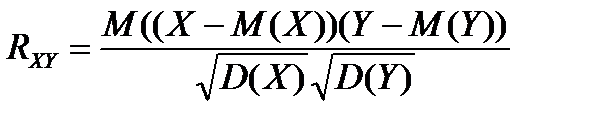
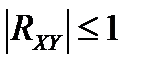 .
. и
и  связаны линейной зависимостью: при
связаны линейной зависимостью: при 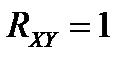 рост значений одной случайной величины сопровождается ростом значений другой, при
рост значений одной случайной величины сопровождается ростом значений другой, при 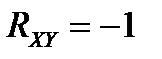 рост значений одной случайной величины сопровождается уменьшением значений другой.
рост значений одной случайной величины сопровождается уменьшением значений другой.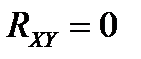 . Обратное утверждение неверно, т.е. при значении коэффициента корреляции равном нулю случайные величины
. Обратное утверждение неверно, т.е. при значении коэффициента корреляции равном нулю случайные величины  сходится по вероятности к случайной величине
сходится по вероятности к случайной величине  , если для любого
, если для любого 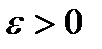 и для любого
и для любого  найдётся такое
найдётся такое 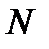 , что при всех
, что при всех 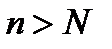 вероятность того, что
вероятность того, что 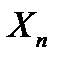 будет отличаться от
будет отличаться от 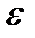 , будет больше, чем
, будет больше, чем 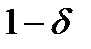 :
: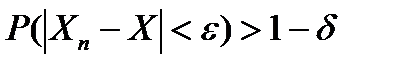

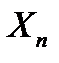 к
к 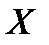 символически часто обозначается так:
символически часто обозначается так: 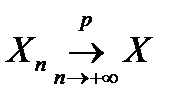
 из того, что последовательность
из того, что последовательность 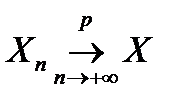 следует, что последовательность
следует, что последовательность 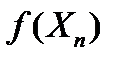 сходится по вероятности к
сходится по вероятности к 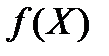 , т.е.
, т.е. 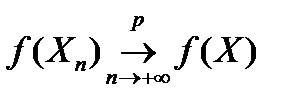 . В частности, это свойство справедливо для линейных функций и возведения в квадрат:
. В частности, это свойство справедливо для линейных функций и возведения в квадрат: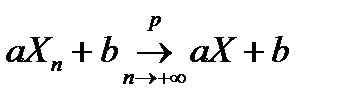 и
и 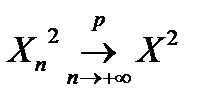 .
.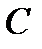 , т.е.
, т.е. 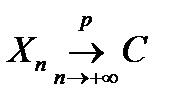 . Такая сходимость равносильна сходимости последовательности
. Такая сходимость равносильна сходимости последовательности 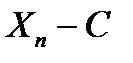 к
к 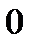 , т.е.
, т.е. 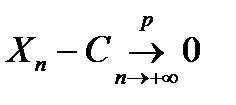 .
.
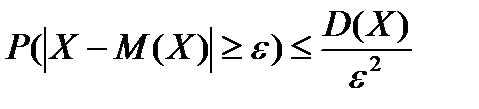
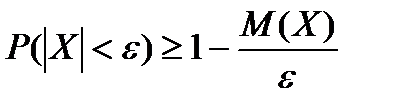
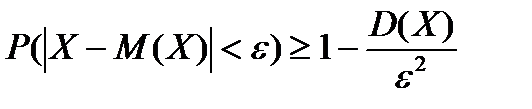
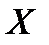 примет значение за пределами интервала
примет значение за пределами интервала  вокруг математического ожидания
вокруг математического ожидания  :
: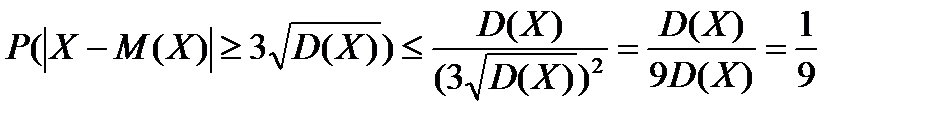 .
.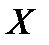 не менее чем на
не менее чем на 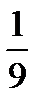 . Следовательно, для любой случайной величины вероятность иметь значение в окрестности
. Следовательно, для любой случайной величины вероятность иметь значение в окрестности  . При этом существуют случайные величины, значения которых внутри этой окрестности лежат с существенно большими вероятностями.
. При этом существуют случайные величины, значения которых внутри этой окрестности лежат с существенно большими вероятностями. испытаний, каждое из которых осуществляется независимо от каждого из остальных и в каждом из которых одно и то же событие
испытаний, каждое из которых осуществляется независимо от каждого из остальных и в каждом из которых одно и то же событие 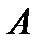 осуществляется с одной и той же вероятностью
осуществляется с одной и той же вероятностью 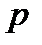 . По сложившейся традиции осуществление события
. По сложившейся традиции осуществление события 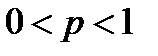 . Осуществление противоположного события
. Осуществление противоположного события 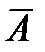 называется неудачей, его вероятность равна
называется неудачей, его вероятность равна  .
.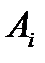 результат i-ого испытания, который может быть либо
результат i-ого испытания, который может быть либо 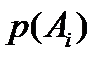 равна либо
равна либо 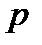 , либо
, либо 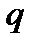 , в зависимости от того, осуществилось событие
, в зависимости от того, осуществилось событие 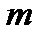 - это число успехов в
- это число успехов в 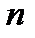 испытаниях, то последовательность
испытаниях, то последовательность 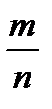 сходится по вероятности к вероятности успеха
сходится по вероятности к вероятности успеха 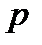 , т.е.
, т.е.  .
. математическое ожидание равно
математическое ожидание равно 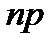 , а дисперсия равна
, а дисперсия равна 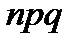 .
.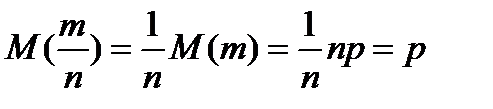 ,
, 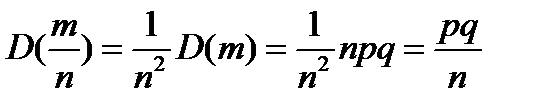 .
.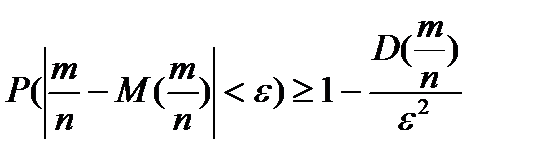 , т.е.
, т.е. 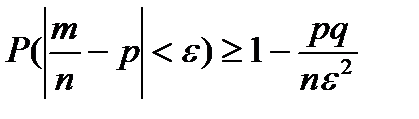
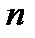 , что
, что  , потому что при увеличении
, потому что при увеличении 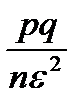 может стать сколь угодно малой. Тогда для любого
может стать сколь угодно малой. Тогда для любого  , потому что верно, что
, потому что верно, что  , т.е.
, т.е. 


