
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия случайной величины и его свойства
Дисперсия случайной величины характеризует уровень отклонений её значений от среднего значения, можно сказать, что дисперсия характеризует степень рассеяния значений случайной величины. Дисперсия важна в оценке распределения любой случайной величины, потому что её распределение существенно меняется, когда значения лежат, например, рядом со средней, т.е. её математическим ожиданием, или когда они довольно сильно могут от этой средней отклоняться. Таким образом, дисперсия Для того, чтобы эту идею оценки отклонения от средней для значений случайной величины превратить в формулу, пришлось проверить на адекватность несколько их вариантов. В каждой из таких формул должно быть отклонение, т.е. разность между значением случайной величины и её математическим ожиданием, и такие разности должны быть тем или иным образом усреднены. В итоге стало общепринятым такое определение дисперсии любой случайной величины X: Можно доказать, что вычислять дисперсию случайной величины можно так: Следует учитывать, что если случайная величина имеет размерность, например, метры или килограммы, то её дисперсия имеет размерность – квадрат исходной, т.е. квадратные метры или квадратные килограммы. В практических вычислениях характеристик случайных величин это не всегда удобно, в таких случаях дисперсию заменяют корнем квадратным из неё, и называют среднеквадрати́ческим отклоне́нием или станда́ртным отклоне́нием этой случайной величины. Обычно это стандартное отклонение обозначают буквой
Пример. Снова вернёмся к предыдущему примеру и вычислим дисперсии определённой в нём случайной величины – числа районов, в которых обнаружена нефть. Дисперию этой случайной величины будем вычислять по формуле
Теперь просуммируем по строке все произведения квадратов числа районов на вероятности и получим математическое ожидание величины Свойства дисперсии Свойства дисперсии одинаковы для всех типов случайных величин, как и для математических ожиданий. 1. 2. 3. 4.
5. 6.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.232 (0.005 с.) |
 . Иначе говоря, дисперсия случайной величины – это математическое ожидание такой составной случайной величины – квадрата разности между данной случайной величиной и её математическим ожиданием. Эта разность между данной случайной величиной и её математическим ожиданием является тоже случайной величиной, сдвинутой так, чтобы её математическое ожидание стало равно нулю. А математическое ожидание этой составной случайной величины и обеспечивает необходимое для определения дисперсии усреднение. В квадрат разность между данной случайной величиной и её математическим ожиданием пришлось возвести, чтобы в сумме отклонений от средней не уничтожались отклонения разных знаков. В формуле определения дисперсии такие отклонения разных знаков суммируются с предварительным возведением их в квадрат.
. Иначе говоря, дисперсия случайной величины – это математическое ожидание такой составной случайной величины – квадрата разности между данной случайной величиной и её математическим ожиданием. Эта разность между данной случайной величиной и её математическим ожиданием является тоже случайной величиной, сдвинутой так, чтобы её математическое ожидание стало равно нулю. А математическое ожидание этой составной случайной величины и обеспечивает необходимое для определения дисперсии усреднение. В квадрат разность между данной случайной величиной и её математическим ожиданием пришлось возвести, чтобы в сумме отклонений от средней не уничтожались отклонения разных знаков. В формуле определения дисперсии такие отклонения разных знаков суммируются с предварительным возведением их в квадрат. . В практических вычислениях дисперсий случайных величин именно такая формула позволяет делать меньше арифметических действий и даёт более результат с более высокой точностью, чем при использовании формулы для определения дисперсии.
. В практических вычислениях дисперсий случайных величин именно такая формула позволяет делать меньше арифметических действий и даёт более результат с более высокой точностью, чем при использовании формулы для определения дисперсии.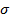 , по определению стандартное отклонение случайной величины X равно:
, по определению стандартное отклонение случайной величины X равно:  . Стандартное отклонение случайной величины имеет размерность ту же, что и сама случайная величина.
. Стандартное отклонение случайной величины имеет размерность ту же, что и сама случайная величина. :
:  . Поскольку математическое ожидание величины
. Поскольку математическое ожидание величины  нам уже известно – 2,4, мы можем его возвести в квадрат и вычесть из
нам уже известно – 2,4, мы можем его возвести в квадрат и вычесть из  . Тогда получится значение дисперсии случайной величины
. Тогда получится значение дисперсии случайной величины  . Дополнительно подсчитаем и стандартное отклонение случайной величины
. Дополнительно подсчитаем и стандартное отклонение случайной величины  . Поскольку дисперсия была меньше единицы, корень из неё получился несколько больше дисперсии, но тоже меньшим единицы.
. Поскольку дисперсия была меньше единицы, корень из неё получился несколько больше дисперсии, но тоже меньшим единицы.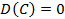 , где C – это константа, т.е. дисперсия константы равно нулю, потому что значения такой случайной величины вообще не отклоняются от её средней.
, где C – это константа, т.е. дисперсия константы равно нулю, потому что значения такой случайной величины вообще не отклоняются от её средней. т.е. дисперсия любой случайной величины всегда неотрицательна.
т.е. дисперсия любой случайной величины всегда неотрицательна. , если случайные величины независимы. Тогда дисперсия их суммы равна сумме их дисперсий.
, если случайные величины независимы. Тогда дисперсия их суммы равна сумме их дисперсий. , где a – это какое-то число. Значит, число можно выносить из под знака дисперсии с возведением этого числа в квадрат.
, где a – это какое-то число. Значит, число можно выносить из под знака дисперсии с возведением этого числа в квадрат. , где a и b – это числа, это следствие из предыдущих свойств дисперсии.
, где a и b – это числа, это следствие из предыдущих свойств дисперсии.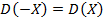 , т.е. дисперсия является чётной функцией от случайной величины – не имеет значения, вычисляется дисперсия от самой случайной величины или противоположной ей по значениям (со знаками минус). Обе эти дисперсии будут равны.
, т.е. дисперсия является чётной функцией от случайной величины – не имеет значения, вычисляется дисперсия от самой случайной величины или противоположной ей по значениям (со знаками минус). Обе эти дисперсии будут равны.


