
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность распределения вероятностей случайной величины
Вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Это получается потому, что в соответствии с 4 свойством функции распределения случайной величины вероятность попадания её значения в этот интервал равна приращению значений функции распределения на этом интервале. Скорость изменения непрерывной функции равна её производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x, x + Δx):
Пусть X – непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим её на Δx и перейдём к пределу при Δx→0:
Если этот предел существует, то он равен производной от функции распределения F(x):
Функция p(x) называется плотностью распределения вероятностей случайной величины X. Из определения следует, что при малых значениях Δx справедливо равенство:
Плотность распределения случайной величины имеет следующие основные свойства: 1. Плотность распределения случайной величины всегда неотрицательна 2. Значения функции распределения случайной величины можно вычислить интегрированием её плотности распределения от
Это свойство можно обосновать так. Поскольку
При этом вычислении мы воспользовались вторым свойством функции распределения: 3. Вероятность попадания значения случайной величины в интервал
Дело в том, что по свойству 4 функции распределения случайной величины 4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице:
Это равенство представляет собой условие нормировки вероятностей для непрерывных случайных величин. Если в соответствии со свойством 2 функции распределения вычислять этот интеграл, то по формуле Ньютона-Лейбница получится:
В некоторых случаях случайные величины принимают значения не на всей действительно оси от Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения случайной величины. Для иллюстрации геометрического смысла перечисленных выше свойств приведём пример графика плотности распределения вероятностей и ниже – график соответствующей функции распределения вероятностей.
Как видно из этих графиков – значение функции распределения в точке a, т.е. F(a) равняется площади под графиком плотности распределения, левее точки a. Это получается потому, что функция распределения F(x) является первообразной функции плотности вероятностей p(x) для одной и той же случайной величины. Кроме того, графики показывают, что графики обеих эти функций лежат выше оси абсцисс, потому что их значения всегда неотрицательны. При этом ещё график функции распределения демонстрирует её неубывание, т.е. рост или в крайнем случае сохранение предыдущих значений при движении слева направо по оси абсцисс. Вероятность попадания значения случайной величины в интервал [a; b) численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (показано на рисунке ниже, на котором плотность вероятности обозначена f(x)).
Площадь всей криволинейной трапеции, заключённой между осью абсцисс и графиком плотности распределения при изменении аргумента от от
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.107.241 (0.007 с.) |
 .
.


 , потому что функция распределения F(x) всегда неубывающая фукнция, а плотность распределения – её производная.
, потому что функция распределения F(x) всегда неубывающая фукнция, а плотность распределения – её производная. до значения аргумента:
до значения аргумента:
 , то
, то  является первообразной
является первообразной 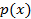 . Тогда этот интеграл можно вычислить по формуле Ньютона-Лейбница:
. Тогда этот интеграл можно вычислить по формуле Ньютона-Лейбница:
 .
. равна интегралу от плотности её вероятности с этими пределами:
равна интегралу от плотности её вероятности с этими пределами:
 . И по формуле Ньютона-Лейбница
. И по формуле Ньютона-Лейбница  , потому что F(x) – это первообразная p(x). Поскольку
, потому что F(x) – это первообразная p(x). Поскольку  и
и  равны одному и тому же значению
равны одному и тому же значению  , вероятность попадания значения случайной величины в интервал
, вероятность попадания значения случайной величины в интервал 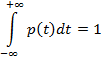

 , а например, на отрезке
, а например, на отрезке  . Тогда всё равно интеграл от плотности вероятности такой случайной величины по всей области её значений будет равен 1. Ведь это как бы «сумма» вероятностей всех возможных элементарных событий, какое-то из них обязательно произойдёт, т.е. какое-то событие обязательно случится, поэтому такая «сумма» вероятностей должна быть равна 1. И для значений случайной величины на отрезке
. Тогда всё равно интеграл от плотности вероятности такой случайной величины по всей области её значений будет равен 1. Ведь это как бы «сумма» вероятностей всех возможных элементарных событий, какое-то из них обязательно произойдёт, т.е. какое-то событие обязательно случится, поэтому такая «сумма» вероятностей должна быть равна 1. И для значений случайной величины на отрезке 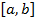 получится:
получится:  .
.




