
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения криволинейных интегралов
1. Длина дуги кривой 2. Масса материальной кривой с
3. Работа силы
4. Площадь фигуры, лежащей в плоскости Оху и ограниченной замкнутой линией L:
где 5. Координаты центра тяжести дуги с линейной плотностью
Пример. Вычислить криволинейный интеграл Решение. Уравнение прямой, соединяющей точки А и В:
Так как кривая L задана уравнением, то криволинейный интеграл I рода, взятый по этой кривой, сводится к определенному интегралу по формуле
Найдем Значит
Пример. Вычислить работу, совершаемую силой
Решение. Воспользуемся формулой
Подставляем данные задачи в эту формулу
Найдем
Тогда
Вычисление таких характеристик полей, как градиент, дивергенция и ротор заключается, как уже было показано ранее, в вычислении соответствующих производных, их переменожении или суммировании и, таким образом, представляет собой некоторое действие (операцию) над полем. Общим свойством этой операции является ее векторный характер. Это свойство можно учесть и в самой форме записи способа вычисления, если определить символический вектор - оператор
который удовлетворяет всем правилам векторной алгебры, т. е. его можно умножать на число (скаляр) или вектор. Знак 1) умножение вектора
2) скалярное умножение
3) векторное умножение
Сравнивая далее (114)-(116) с (79), (92) и (106), получим, что в декартовой системе координат оператор
Определение (1) удобно тем, что оно пригодно для любой системы координат, в то время как (5) - частный случай для декартовой. Оператор
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1094; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.231.245 (0.005 с.) |
 .
.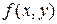 - линейной плоскостью
- линейной плоскостью .
. при перемещении материальной точки вдоль дуги кривой L:
при перемещении материальной точки вдоль дуги кривой L: .
. или
или  или
или  ,
, - интеграл по замкнутому контуру L.
- интеграл по замкнутому контуру L. ;
;  .
. , где L – отрезок прямой, заключенный между точками А(0,-4) и В(2,0)
, где L – отрезок прямой, заключенный между точками А(0,-4) и В(2,0) ,
, 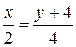 ,
,  ,
, 

 .
.
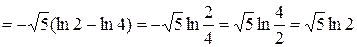 .
. при перемещении материальной точки по дуге кривой
при перемещении материальной точки по дуге кривой  от точки О(0,0) до точки А(2,10).
от точки О(0,0) до точки А(2,10). .
. .
. .
.


 (ед).
(ед). (набла):
(набла):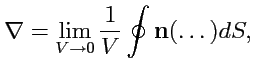
 означает, что при этом соответствующая величина должна быть подставлена сюда вместе с символом векторной операции. Тогда, получим
означает, что при этом соответствующая величина должна быть подставлена сюда вместе с символом векторной операции. Тогда, получим вектор:
вектор:




 - векторы, то выражение
- векторы, то выражение  не имеет смысла, если не указана сответствующая бинарная операции: сумма, скалярное или векторное произведение.
не имеет смысла, если не указана сответствующая бинарная операции: сумма, скалярное или векторное произведение.


