
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров. Точечные оценки.
Пусть θ – неизвестный оцениваемый параметр, а θ* - приближенное значение данного параметра, полученное на основании выборочных данных. Такая оценка θ* параметра θ в виде одного числа, называется точечной оценкой. Точечная оценка называется несмещенной, если М(θ*) = θ, и смещенной - в противном случае. Точечная оценка называется эффективной, если ее дисперсия минимальна среди всех других возможных оценок данного параметра. Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки ее значение неограниченно приближается к оцениваемому параметру. Несмещенной, эффективной и состоятельной оценкой мат. ожидания изучаемого признака является выборочная средняя:
где n– объем выборки. Если объем всей генеральной совокупности равен N, а количественный признак может принимать отдельные изолированные значения, то математическое ожидание
Точечная оценка дисперсии – выборочная дисперсия:
Для расчетов можно применять и другую формулу:
Доказательство: DB=
Выборочная дисперсия является смещенной оценкой, поэтому при малых значениях объема выборки применяют исправленную выборочную дисперсию: Выборочное среднее квадратическое отклонение - смещенная оценка генерального среднего квадратического отклонения:
Исправленное выборочное среднее квадратическое отклонение:
несмещенная оценка генерального среднего квадратического отклонения.
где n=n1 + n2 +…+nk – объем выборки. § 2. Условные варианты. Моменты. Метод произведений Предположим, что варианты выборки расположены в возрастающем порядке, причем – равноотстоящие, т.е. те, которые образуют арифметическую прогрессию с разностью h = xi+1 – xi – шаг выборки (при этом условные варианты будут целыми числами). Условными называют варианты, которые определяются равенством Замечание: если С = хm, то um=0. Обычным эмпирическим моментом порядка k называется величина
Начальным эмпирическим моментом порядка k называется обычный момент порядка k при с=0: Замечание: очевидно, что М1 =
Центральным эмпирическим моментом порядка k называется обычный момент порядка k при c= Замечание: очевидно, что m2 = DB. Теорема1: m2 = M/2 – (M/1)2.
Условным эмпирическим моментом порядка k называется начальный момент порядка k, вычисленный для условных вариант: Теорема2: если С – ложный ноль, h – шаг выборки,
Метод произведений применяется для вычисления условных моментов, следовательно, и для вычисления
1. В 1ом столбце записывают выборочные (первоначальные) варианты в возрастающем порядке. 2. Во 2ом - записывают частоты этих вариант. 3. В 3ем – записывают условные варианты 4. В 4ом – вычисляют произведения niui. 5. В 5ом – вычисляют произведения niu 6. Далее суммируют вычисления по столбцам, записывая результаты снизу. 7. Вычисляют условные моменты Замечание: можно добавить 6ой столбец, в котором вычисляют произведения ni(ui+1)2. Внизу, просуммировав, получают Пример. Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х i, а во второй строке – соответственные частоты n i количественного признака Х). Требуется найти: 1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение. 2. Доверительный интервал для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.
Решение: 1. Для нахождения
Вычислим условные моменты: Теперь, зная ложный ноль С=280 и шаг выборки h=270 – 260 =10, вычисляем выборочную среднюю: 2. Доверительный интервал. DВ=160 Þ s= Пользуясь таблицей приложения 3 по g = 0,95 и n = 100 находим tg=1,984, тогда искомый доверительный интервал Ответ: 1. а)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.240.21 (0.018 с.) |
 ,
, .
. .
.
 , где
, где  вычисляют по формуле:
вычисляют по формуле:  .
. .
. .
. -
- , где С – ложный ноль (новое начало отсчета). В качестве ложного нуля можно взять любую варианту, но максимальная простота вычислений достигается, если она находится примерно в середине вариационного ряда и имеет наибольшую частоту.
, где С – ложный ноль (новое начало отсчета). В качестве ложного нуля можно взять любую варианту, но максимальная простота вычислений достигается, если она находится примерно в середине вариационного ряда и имеет наибольшую частоту. , где ni – частоты, xi – значения вариант, с – некоторое значение, n – объем выборки. В частности,
, где ni – частоты, xi – значения вариант, с – некоторое значение, n – объем выборки. В частности,  .
.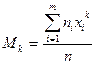 . В частности,
. В частности, 
 .
. . В частности,
. В частности,  .
. .
.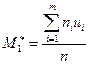 и
и  - условные эмпирические моменты соответственно 1го и 2го порядков, то выборочная средняя равна
- условные эмпирические моменты соответственно 1го и 2го порядков, то выборочная средняя равна  , выборочная дисперсия:
, выборочная дисперсия:  .
. . Для простоты вычислений целесообразно воспользоваться расчетной таблицей вида:
. Для простоты вычислений целесообразно воспользоваться расчетной таблицей вида:
 .
. . Если
. Если  + 2
+ 2 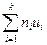 + n, то вычисления произведены правильно.
+ n, то вычисления произведены правильно.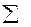
 =0,4;
=0,4;  =1,76.
=1,76.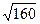 »12,65.
»12,65. =
=  » 12,71.
» 12,71. примет вид:
примет вид:  , т.е.
, т.е.  .
.


