
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассуждение считается правильным, если из истинных посылок не может следовать ложного заключения.
Так как каждая посылка- это высказывание, то оно может быть записано в виде формулы. Следовательно, рассуждение – это последовательность формул. Заключение тоже является формулой. Если
И будем говорить, что из посылок логически следует заключение. Нас будет интересовать только форма рассуждения, а не конкретное содержимое каждого высказывания, и на основании анализа формы мы будем делать вывод о том, правильное или неправильное рассматриваемое рассуждение. Если рассуждение признается правильным, то все рассуждения, приведенные по этой формуле, правильны, независимо от того, к какой предметной области они относятся. Теорема.Рассуждение (1) правильно тогда и только тогда, когда формула Доказательство: Достаточность: Если (2) -это тавтология, то конъюнкция посылок не может быть равно 0, значит Необходимость: Если (1) правильно, то из истинности посылок Что и требовалось доказать. Пример 1: пусть имеется рассуждение 1. Если многоугольник правильный, то в него можно вписать окружность. 2. Данный многоугольник правильный. 3. Следовательно, в него можно вписать окружность. Введем обозначения: р - многоугольник правильный. q - в многоугольник можно вписать окружность. Посылки: Рассуждение принимает вид: Формула, соответствующая этому рассуждению: ( Установим вид этой формулы. Сняв импликацию, получим:
Следовательно, рассуждение правильное. Рассуждения, построенные по формуле ( ( Пример 2: пусть имеется рассуждение 1. Если многоугольник правильный, то в него можно вписать окружность. 2. В многоугольник нельзя вписать окружность. 3. Следовательно, он неправильный.
Используя обозначения предыдущего примера, получим формулу, соответствующую этому рассуждению: ( Аналогично предыдущему установим, что эта формула - тавтология, значит рассуждение правильное. Данная формула называется правилом отрицания (ПО). ( Пример 3: пусть имеется рассуждение Если многоугольник правильный, то в него можно вписать окружность, следовательно, если в многоугольник нельзя вписать окружность, то он неправильный. Рассуждение Доказательство: Соответствующая формула ( Данная формула называется правилом контрапозиции (ПК). ( Пример 4: пусть имеется рассуждение Если в треугольнике все стороны равны, то он равносторонний. Если треугольник равносторонний, то углы равны 60 Введем обозначения: р - в треугольнике стороны равны. q – треугольник равносторонний. r – углы равны 60 Рассуждение Соответствующая формула: ( Данная формула называется правилом силлогизма (ПС). ( Замечание. Полученные формулы называются правилами вывода. Правило вывода иногда записывают в виде: ПЗ: ПС: Другие правила вывода: · Доказательство. р · Доказательство. рq · Доказательство. рq
· Доказательство.
Существуют и другие правила вывода Замечание: Так как правила вывода являются тавтологиями, то подстановка вместо элементарного высказывания любой формулы даст нам тавтологию, каждая из которых может быть объявлена правилом вывода. Вывод. Вывод- это последовательность формул, каждая из которых является посылкой или получена из предыдущих формул на основе правил вывода. Последняя формула есть заключение. Пример: пусть имеется рассуждение 1. Если прямая не имеет общих точек с плоскостью, то она параллельна этой плоскости.
2. Если прямая имеет две общих точки с плоскостью, то она принадлежит этой плоскости. 3. Прямая не параллельна плоскости и не принадлежит ей, следовательно, она имеет одну общую точку и пересекает плоскость. Введем обозначения: х – прямая не имеет общих точек с плоскостью. у – прямая параллельна плоскости. z – прямая имеет две общих точки с плоскостью. u – прямая принадлежит плоскости. Рассуждение имеет вид: х Построим вывод. 1) 2) 3) 4) х 5) 6) z 7) 8) Теорема дедукции. Теорема. Пусть дано Тогда Доказательство: Так как рассуждение (1) правильное, то из истинности посылок не может следовать ложного заключения. Предположим, что рассуждение (2) неправильное. Тогда из истинности посылок Что и требовалось доказать. Пример 1: Рассмотрим ПО: р По теореме дедукции р Пример 2 Рассмотрим рассуждение. рr По теореме дедукции: рr 1) р 2) р – УК (1); 3) 4) р r 5) 6) Формула Предикаты. При анализе рассуждений в логике высказываний нас не интересовала внутренняя структура самих высказываний. И это обстоятельство не позволяет анализировать большое количество рассуждений. Например: Через две данных точки проходит единственная прямая. Точка лежит между двумя точками. х>5. Эти предложения не являются высказываниями, но становятся таковыми, если предметным переменным, входящим в эти предложения, задать конкретны значения. Так в последнем примере при х = 3 получим ложное высказывание, а при х = 8 истинное высказывание. Значения предметных переменных берутся из некоторого предметного множества А (точек, углов, прямых, чисел, ромбов и т.д.). Введем понятие предиката. Под предикатом предметной переменной х Например: Предикат х > 5, x Функция Р (х, у), где х, у Например: х<у Пусть У = 5, получим х < 5 – одноместный предикат. Если положить х = 4, то 4 < 5 – нульместные предикаты (высказывания). Местность предиката - количество предметных переменных. Задание конкретного значения предметным переменным понижает местность предиката. Одноместные предикаты выражают свойство быть чем-то. Например: Свойство быть точкой. х – точка. Введем обозначение этого предиката: Т (х). Тогда Т (А) читается как А-точка. Двухместные предикаты и предикаты более высокой местности выражают отношения между объектами. Например: Двухместный предикат принадлежности – х Если х – точка, а у – прямая, то читаем: точка х принадлежит прямой у.
Выбор предикатного символа остается за пользователем. Так, вместо х Пусть на множестве U задан предикат Р (х). Задавая х различные значения, мы будем получать высказывания, часть из которых истинна, а часть возможно ложна. Множество М Операции над предикатами. Над предикатами выполняются те же операции, что и над высказываниями. 1) Отрицание.
Рис. 1. Область истинности отрицания предиката
2 ) Конъюнкция Р (х)
Рис. 2. Область истинности конъюнкция предикатов
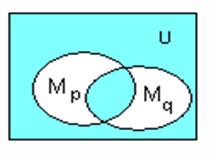
3) Дизъюнкция Р (х)
Рис. 3. Область истинности дизъюнкции предикатов
4) Импликация Р (х)
Рис. 3. Область истинности импликаци предикатов 5) Эквиваленция Р (х)
Рис. 4. Область истинности эквиваленции предикатов Кванторы. Рассмотрим предложения: В любой треугольник можно вписать окружность. Всякое число, оканчивающееся на четную цифру, делится на 2. В этих предложениях встречаются слова «любой», «всякое». Эти слова заменяют специальным символом. Значок
( Например. Пусть Р (х) предикат, выражающий для х Наряду с квантором всеобщности в логике предикатов рассматривается квантор существования: Его значок
( Например. Пусть Р (х) предикат, выражающий для х Операция введения квантора называется операцией навешивания квантора. Навешивание квантора по какой-нибудь переменной понижает местность предиката. Переменная, по которой навешен квантор, называется связанной. Например. х<у - двухместный предикат. Навесим квантор: ( Таким образом, понизить местность предиката можно двумя способами. 1. задать предметной переменной конкретное значение. 2. навесить кванторы по одной или нескольким переменным. Квантор всеобщности можно рассматривать как обобщение конъюнкции для конечных и бесконечных множеств. Квантор существования можно рассматривать как обобщение дизъюнкции для конечных и бесконечных множеств. Операции с кванторами. Пусть имеется предикат х<у, где х, у 1) ( 2) ( 3) ( 4) ( 5) ( 6) ( 7) ( 8) ( Таким образом, видим, что одноименные кванторы можно менять местами, не изменяя значения предиката. Изменение порядка разноименных кванторов приводит к изменению истиностного значения предиката. Формулы. Понятие формулы в логике предикатов введем аналогично понятию формулы в логике высказываний. 1) Всякая высказывательная переменная есть формула. 2) Предикатный символ есть формула. 3) Если 4) Если ( 5) Других формул нет.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.50 (0.131 с.) |
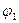 ,
,  ,…,
,…, 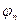 -это последовательность посылок. а
-это последовательность посылок. а 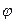 - заключение, то будем писать
- заключение, то будем писать
 . (1)
. (1)
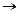
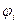 не может следовать ложного заключения
не может следовать ложного заключения 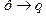 , р. Заключение – q.
, р. Заключение – q. , р ├ q.
, р ├ q.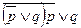
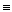 (по законам де Моргана)
(по законам де Моргана) 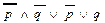
 (снимая двойное отрицание)
(снимая двойное отрицание) 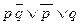
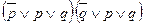 . Это КНФ. Каждая элементарная сумма содержит высказывание со своим отрицанием, значит формула – тавтология.
. Это КНФ. Каждая элементарная сумма содержит высказывание со своим отрицанием, значит формула – тавтология.
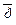 .
.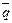
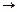
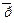 (ПО).
(ПО). (
(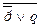 )
) 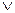

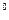 , следовательно, если в треугольнике стороны равны, то углы по 60
, следовательно, если в треугольнике стороны равны, то углы по 60 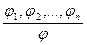 .
.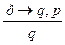 , ПО:
, ПО: 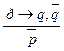 , ПК:
, ПК: 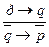 ,
, 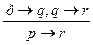 .
.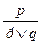 - введение дизъюнкции (ВД).
- введение дизъюнкции (ВД).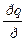 - удаление конъюнкции (УК).
- удаление конъюнкции (УК).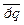
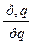 - введение конъюнкции. (ВК)
- введение конъюнкции. (ВК)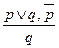 удаление дизъюнкции (УД).
удаление дизъюнкции (УД).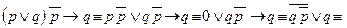
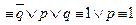
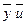 ├
├ 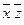 .
.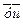 - посылка.
- посылка.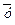 - УК (из 1);
- УК (из 1);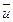 - УК (из 1);
- УК (из 1); - ПО (из 4 и 2);
- ПО (из 4 и 2);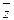 - ПО (из 6 и 3);
- ПО (из 6 и 3);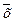
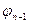 ├
├  .
.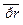 - ПО (4,3), т.е.
- ПО (4,3), т.е. 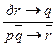 называется правилом расширенной контрапозиции (ПРК).
называется правилом расширенной контрапозиции (ПРК). А будем понимать функцию Р(х) на {0,1}. Предикат р (х) называется одноместным предикатом
А будем понимать функцию Р(х) на {0,1}. Предикат р (х) называется одноместным предикатом (х) значений х, при которых предикат Р - истина, называется областью истинности.
(х) значений х, при которых предикат Р - истина, называется областью истинности. - предикат, множеством истинности которого является множество, для которого предикат Р – ложный.
- предикат, множеством истинности которого является множество, для которого предикат Р – ложный.
 .
.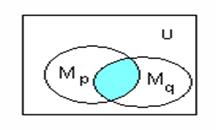
 М
М 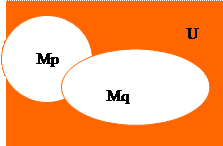
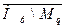 ).
).
 Q(х) – предикат, область истинности которого совпадает с объединением пересечения М
Q(х) – предикат, область истинности которого совпадает с объединением пересечения М 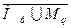 .
.
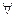 называется квантором всеобщности.
называется квантором всеобщности.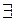 .
. х) (х
х) (х  ,
, 


