
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства Декартового произведения.Стр 1 из 15Следующая ⇒
1) А Х В≠В Х А. 2) (А Х В) Х С≠А Х (В Х С). 3) А Х (В∩С)=(А Х В)∩(А Х С). 4) А Х (В 5) (А∩В) Х С=(А Х С) ∩(В Х С). 6) (А 7) А Х (В\С)=(А Х В)\(А Х С). 8) (А\B) X C= (A X C)\ (B X C). Доказательство свойства 3.: Обозначим А Х (В∩С)=D1 и (А Х В)∩(А Х С)= D2. a) Пусть z b) Пусть (x,y) По теореме о равенстве множеств D1= D2. Что и требовалось доказать. Остальные свойства доказывается аналогично предыдущему Отношения. Пусть заданы два множества А и В. Найдем А Х В. Подмножество k Отношения задаются знаками =, <, >, Пример: А={2,3,4}, B={1,4,3} A X B={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)} Выделим отношения больше > и меньше <
Рис.11. Отношение >. Композиция отношений. Пусть отношение Композицией этих отношений является отношение k = Композицией отношений из А в В называется множество пар (а,b) таких, что, а Пример: А={2,3,4}, B={1,4,3}, С={2,5} A X В={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)} A X C={(2,2),(2,5),(3,2),(3,5),(4,2),(4,5)} C X B={(2,1),(5,1),(2,4),(5,4),(2,3),(5,3)} Определим отношение >: Возьмем пару (3,2) Берем пару (4,2) Получим k= Таким образом, для элемента (2,4) Отношения на множестве. Если в декартовом произведении в качестве множества В выбрать множество А (то есть А Х А= А Для отношений на множестве вводятся понятия: Обратное отношение -это множество пар (а,b) таких, что (b,a)
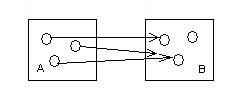
Дополнение -это множество пар (а,b) Тождественное отношение -множество пар (а, а) таких, что, а I= {(a, a), a Универсальное отношение U ={(a,b),a Виды отношений: Инъекция. Если каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным.
Рис.12.Инъекция.
Сюръекция.
Рис.13.Сюръекция.
Биекция. Если для каждого элемента y Биективное отношение инъективно и сюръективно. Биективное отношение имеет обратное отношение.
Рис.14. Биекция.
Функции.
Пусть заданы множества А и В. Найдем А Х В. Выберем отношение f Способы задания: А Пример: А={2,3,4}, B={1,4,3}
Рис.15.Функция Комбинаторика.
Задачи, в которых требуется определить количество возможных операций, называется комбинаторными. Пусть имеется группа некоторых объектов Из этой группы элементов будем образовывать подгруппы. Такие подгруппы будем называть соединениями. Из этих соединений выделим классы, которые будем называть размещениями. Размещения.
Размещениями из m -элементов по n называются соединения, каждое из которых содержит n элементов, взятых из данных m и которые отличаются друг от друга или элементами, или их порядком.
Предполагается, что элементы водном размещении не повторяются.
|
||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.244.83 (0.025 с.) |
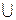 С)=(А Х В)
С)=(А Х В)  D1, z- элемент декартового произведения, z=(x,y), где х
D1, z- элемент декартового произведения, z=(x,y), где х  А Х В называется отношением из множества А во множество В.
А Х В называется отношением из множества А во множество В.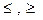 и т.д.
и т.д.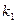 ={(2,1),(3,1),(4,1),(4,3)}
={(2,1),(3,1),(4,1),(4,3)}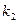 ={(2,4),(2,3),(3,4)}
={(2,4),(2,3),(3,4)}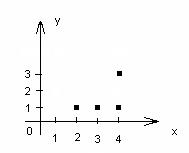
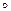
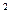 ), то отношение k из А
), то отношение k из А 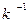
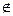 k. Обозначение
k. Обозначение 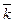
 Если для каждого элемента y множества В существует элемент х
Если для каждого элемента y множества В существует элемент х 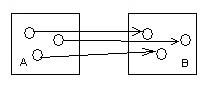
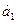 ,
, 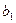 ),(
),(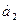 ,
,  ),…}, состоящее из пар таких, что
),…}, состоящее из пар таких, что 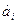 ≠
≠ 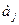 , i=1,2,3,…., то есть отношение, в которой все первые элементы пар различны. Такие отношения называются функциями.
, i=1,2,3,…., то есть отношение, в которой все первые элементы пар различны. Такие отношения называются функциями.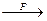 В; f: A
В; f: A  B; b=f (a); a f b.
B; b=f (a); a f b.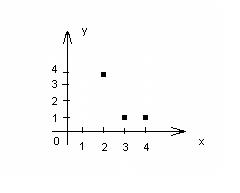 A X В={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)}
A X В={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)}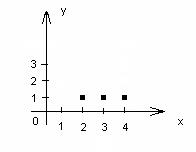 Выделим: функции
Выделим: функции 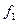 ={(2,1),(3,1),(4,1)} и
={(2,1),(3,1),(4,1)} и 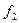 ={(2,4),(3,1),(4,1)}
={(2,4),(3,1),(4,1)}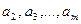 , которые мы будем называть элементами.
, которые мы будем называть элементами.


