
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм Фано для префиксного кодирования.
Пусть кодируемое сообщения таково, что известны вероятности вхождения каждого символа, причем То есть прежде чем производить кодирование, необходимо расположить буквы алфавита А так, чтобы удовлетворялось условие (1). Затем проверить равенство (2), после чего назначать коды. Итак, имеем
….
….
Алгоритм. Разобьем вероятности на две части так, чтобы суммы вероятностей каждой из частей были примерно равны. Пусть это будет после Полученная схема кодирования является префиксной, так как код первой строки и код второй строки отличаются друг от друга, по крайней мере, в последнем знаке, то эти коды не могут быть префиксами друг друга. Аналогично, так как в верхней части разбиения добавляется 0, а в нижней 1, то ни один из кодов верхней части не может быть префиксом кода нижней части. Таким образом, схема префиксная, следовательно, разделимая. Пример: пусть заданы вероятности 0,25 0,15 0,112 0,11 0,08 0,06 0,06 0,06 0,06 0,05. После первого разбиения получим вероят- ности коды 0,25 0 0,15 0
0,11 1 0,08 1 0,06 1 0,06 1 0,06 1 0,06 1 0,05 1 после второго разбиения вероят ности ти коды
0,15 0 01
0,11 1 0,08 1 0,06 1 0,06 1 0,06 1 0,06 1 0,05 1
После третьего разбиения
0,11 1 0,08 1 0,06 1 0,06 1 0,06 1 0,06 1 0,05 1
После четвертого разбиения
0,11 1 1 10 0,08 1 1 10
0,06 1 1 11 0,06 1 1 11 0,06 1 1 11 0,05 1 1 11
Окончательно получим:
0,05 1 1 11 11 11 111 111 1111
Если кодирование равномерное, то цена кодирования по формуле Хартли равна: Оптимальное кодирование. При использовании кодирования по алгоритму Фано мы получаем некоторую цену кодирования. Так как разбиение на две части неоднозначно, то цена кодирования может меняться, то есть является некоторой функцией длины элементарных кодов. А так как эта цена кодирования конечна, то она имеет наименьшее значение. Кодирование, при котором цена кодирования имеет наименьшее значение, называется оптимальным. Т.к. число вариантов кодирования конечно, то оптимальное кодирование существует. Таким образом, алгоритм Фано дает кодирование близкое к оптимальному. Рассмотрим несколько вопросов, относящихся к оптимальному кодированию. Лемма 1. Пусть имеется распределение вероятностей Тогда для любого j>i имеем: Доказательство: Пусть существует такое j, что
Лемма 2. Пусть имеется распределение вероятностей (1) Доказательство: Допустим, что код максимальной длины один. По лемме 1
Докажем теперь, что два кода наибольшей длины отличны только лишь в последнем разряде: Пусть
|
||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.214 (0.018 с.) |
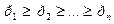 ( 1), причем
( 1), причем 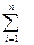
 =1 (2)
=1 (2)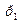 = 0,…
= 0,…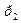 = 0,…
= 0,…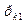 = 0,….
= 0,….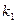 вероятности:
вероятности: 
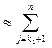
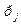 . Назначим коды: в верхней части 0, а в нижней 1. Теперь разбиваем верхнюю часть на две части, с примерно равными суммами вероятности:
. Назначим коды: в верхней части 0, а в нижней 1. Теперь разбиваем верхнюю часть на две части, с примерно равными суммами вероятности: 

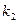 0,25 0 00 код назначен
0,25 0 00 код назначен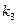 0,15 0 01 010 код назначен
0,15 0 01 010 код назначен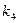 0,06 1 1 10
0,06 1 1 10 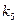 0,11 1 1 10 100
0,11 1 1 10 100 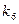 0,08 1 1 10 101 1010
0,08 1 1 10 101 1010  0,06 1 1 11 11 11 110 1100
0,06 1 1 11 11 11 110 1100 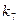 0,06 1 1 11 11 11 110 1101
0,06 1 1 11 11 11 110 1101 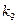 0,06 1 1 11 11 11 111 111 1110
0,06 1 1 11 11 11 111 111 1110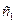 = log
= log 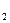 10
10 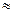 4. По алгоритму Фано:
4. По алгоритму Фано: 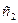 =
= 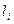 =3,12, что меньше 4, а значит, общая длина кода будет меньше.
=3,12, что меньше 4, а значит, общая длина кода будет меньше.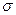 ={
={ 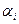
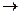
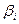 }|
}| 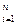 . (2)
. (2)
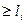 .
.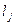 <
< 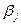 , получим, что
, получим, что ={
={ 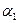
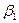 ;…
;… 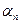
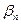 } и С
} и С 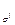 <C
<C 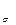 , что противоречит оптимальности кодирования. Значит наше предположение неверно и
, что противоречит оптимальности кодирования. Значит наше предположение неверно и 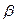 0 или
0 или  =
=  - префикс
- префикс 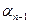
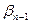 ;…
;… 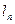 , то
, то 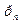 |
| 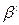
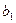 ,
, 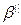
 ,
, 
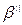 , и так как он не префикс, то его можно выбрать в качестве элементарного кода: |
, и так как он не префикс, то его можно выбрать в качестве элементарного кода: |  , совпадающая с
, совпадающая с 


